Toroid tai Toro Dona

Selitämme, mikä on härkä tai härkä, sen ominaisuudet, tilavuus, pinta, sovellukset ja osoittavat useita esimerkkejä

Mikä on toroidi?

Hän Toroidi Se on kolmen dimensioinen geometrinen runko vanteen, renkaan, renkaan, munkin tai munkin muodossa, joten "Toro Dona" -nimi, joka kuuluu nimeltään objektien luokkaan Vallankumous kiinteät aineet.

Toroidi luodaan kiertämällä suljettua litteää kuviota, linjan ympärillä, joka kuuluu kuvan samaan tasoon, mutta ei sieppata sitä, kuten alla on esitetty:

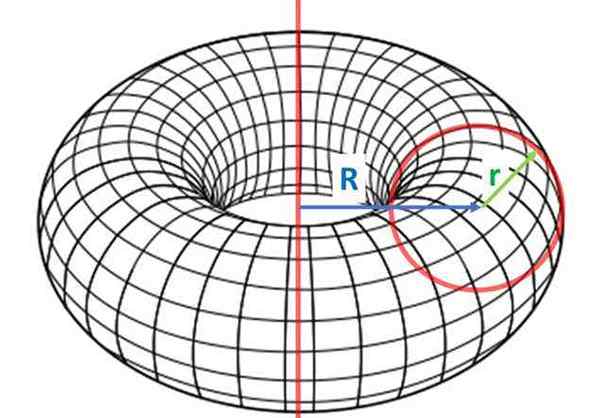
Härkä, joka on vallankumouksen pinta, joka saadaan kiertämällä suljettua litteää kuvaa (kehänä) kiinteän akselin ympärillä. Lähde: Wikimedia Commons

Toroidin pääominaisuus on, että huolimatta suljetusta pinnasta, siinä on reikä. Tämä tarkoittaa, että sen pinnan kaksi pistettä voidaan kytkeä segmentillä, joka on esineen ulkopuolella.

Toinen toroidin ominaisuus on, että se on kolmiulotteinen hahmo ilman kärkipisteitä. Tämä ominaisuus jakaa sen muihin tilavuuskappaleisiin, kuten palloon, mutta vaikka pallo on kupera pinta, härkä on samanaikaisesti kovera ja kupera.

Härän keskuudessa, härkä Se on yleisin ja saadaan radioympyrän kierrosta r -, Etäisyysakselista R - ensimmäisestä. Radio R (pienissä kirjaimissa) tunnetaan vähäinen säde ja R (pääoma) on suurin säde.

Toroidin tilavuus

Härkä syntyy kiertämällä suljettua pinta -alaa -Lla kierto -akselin ympärillä, joka ei leikkaa sitä. Merkitä R - Etäisyys akselista tasaisen kuvion keskikohtaan, vallankumouksen härän tilavuus on:

Voi palvella sinua: Käänteiset trigonometriset toiminnot: arvo, johdannaiset, esimerkit, harjoitukset

V = 2πr⋅ a 

Tämä tulos saadaan levitettäessä Pappuslause Vallankumouksen kiinteän aineen tilavuuden osalta, jonka mukaan minkä tahansa kiinteän vallankumouksen tilavuus saadaan kertomalla kuvan pinta -ala, joka rikkoutuu kehän kehällä, joka muodostuu keskikohdan pyörimisellä (tai painopisteellä ) pyöritetyn kuvan, kierto -akselin ympärillä.

Härän tilavuus

Härkä on radio ympyrän tuottama toroidi r -. Jos kierto -akselin etäisyys ympyrän keskipisteeseen on R, on sitten tarpeen, että härkä on:

V = (2πr) ⋅ (πr²) = 2π²R -³

Härän pinta

Ole yksinkertaisesti liittyvä tasainen kuva -Lla ja muoto Lens. Jos tällaista lukua pyöritetään samassa kuvion tasossa olevaan akseliin, mutta se ei ylitä sitä, niin generoitu pinta on pinta -ala:

S = 2πr⋅ l

Koska etäisyys akselista painopisteeseen tai keskikohtaan, generatrix -luku.

Tämä tulos on seuraus jstk Pappuslause Vallankumouksen pinnalle.

Härän pinta

Radio R: n (pieni kirjain) ja radion pormestari R (isoja) pyöreä ristikkäinen härkä on tietty härkä, nimeltään Toro.

Kuten säteen R ympyrän ääriviivat ovat 2πr, Sitten mainitun härän pinnan pinta -ala on:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Toroidisovellukset

Geometristen ominaisuuksiensa vuoksi härällä on lukemattomia käytännöllisiä ja kulttuurisia sovelluksia. Aluksi vanteet tai renkaat ovat toroidisia osia, joilla on erilaisia ​​käyttötarkoituksia:

Voi palvella sinua: vähimmäisruutuja

Kulttuuri-

• Koristeellinen tai kosmeettinen käyttö, kun rengas asetetaan sormelle tai kun lävistys asetetaan korvaan.
• Härän nenässä asetetaan vanne, joka palvelee sitä ja hallita sitä.
• Kun rengas tai rengas sijoitetaan vasempaan käteen rengas sormelle, niin siinä on sosiaalinen merkitys, joka on peräisin muinaisten kreikkalaisten ajasta, ja se tarkoittaa sitoutumista, uskollisuutta ja avioliittoa pariskunnalle, joka kantaa samassa vannessa ja materiaali.

Mekaniikassa

Koristeellisen, kosmeettisen ja kulttuurisen kontekstin ulkopuolella härällä on monia käytännön sovelluksia. Mekaniikassa toroidia käytetään laakerin retentiorenkaana ajoneuvon akselin kärjessä. 

Myös moottoriajoneuvojen laakerit muodostetaan yhdellä tai kahdella vanteella härkämuodossa, jossa on eri poikkileikkausmuotoja, joihin ne rullaavat sylinterit tai pallot, tarkoituksena vähentää kitkaa akseleilla.

Sähkö

Sähköisissä sovelluksissa toroidi on myös erittäin tärkeä, koska induktorien, sähkömagerien ja muuntajien ferromagneettisilla ytimillä on usein härän muoto ja niissä kaapeli kelan muodossa.

Tokamak

Venäjän nimen nimellä on eräänlainen ohjattu fuusioreaktori toroidin tai munkin muodossa: t: tTaamak. Tämän tyyppisissä ydinfuusioreaktorissa säiliöllä ja keloilla, jotka tuottavat plasman sulkemisen magneettikentän.

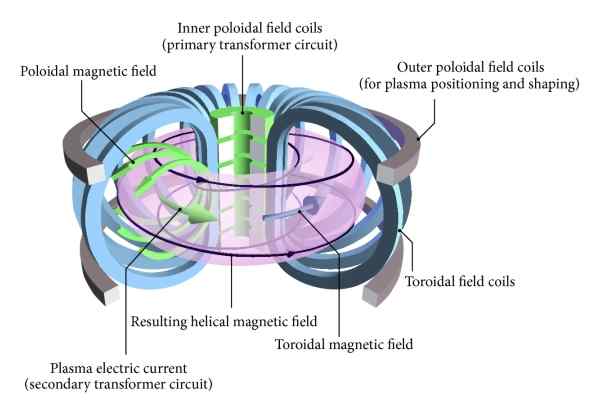Kuvassa on kaavamaisesti kontrolloitua ydinfuusioreaktoria toroidisessa muodossa, joka tunnetaan nimellä "tokamak". Tämän tyyppisissä reaktorissa sekä plasmassa, kelat että synnytyksen magneettikenttä on toroidinen kokoonpano. Lähde: Wikimedia Commons

Esimerkit

Neliömäisen härän pinta (kaavalla)

Tässä esimerkissä neliömäistä härää pidetään seuraavassa kuvassa esitetyllä tavalla:

Voi palvella sinua: Scaleno -kolmio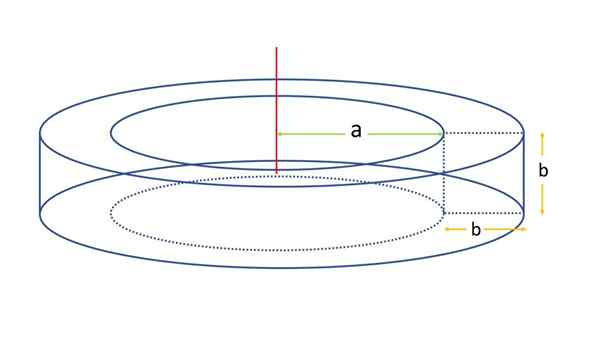 Neliöosa toroidi. Lähde: f. Zapata

Pinta määritetään käyttämällä yleisen härän pintakaavaa. Tätä varten on tarpeen tietää kierto -akselin etäisyys neliön keskikohtaan, mikä edellisen nimikkeistön avulla on R --

R = a + b/2

On myös tarpeen tuntea kehä Lens Generatrix -hahmo, joka on tässä tapauksessa neliö b -, Sen muoto on pitkä:

L = 4⋅B

Sitten härän pintakaava levitetään:

S = 2πr⋅l

R -ja L korvaaminen vastaaville lausekkeille, neliön härän toimenpiteistä A ja B riippuen on:

S = 2π (a + b/2) ⋅4⋅b = 8π (a + b/2) ⋅b

Neliömäinen toroidipinta (sen kasvojen summa)

Edellisen luvun neliömurha koostuu neljästä pinnasta: ylä- ja alempi ovat litteät renkaat ja sisä- ja ulkopinta ovat lieriömäisiä.

Tämän huomioon ottaen on mahdollista laskea sen pinta lisäämällä sen neljän pinnan pinta -ala.

Ylä- ja alapinnoilla on alue, joka on yhtä suuri kuin säteen ulkopiiri (A+B) Vähemmän radion sisäpiiri -lla, joiden seurauksena on:

S_s= S_Yllyttää= π [(a+b)² - b -²] = π⋅ [a²+ 2AB]

Sisäisellä lieriömäisellä kasvolla on alue:

S₁= 2πab

Ja ulkoisella lieriömäisellä kasvolla on alue:

S₂= 2π (a+b) b = 2πab+2πb²

Niin, että toroidin kokonaispinta -ala on summa s_s+S_Yllyttää+S₁+S₂-

A = 2π⋅ [a²+ 2AB]+2πab+2πab+2πb².