Lineaariset muunnokset ominaisuudet, mitkä ovat käyttö, tyypit, esimerkit

Eräs Lineaarinen muuntaminen, jota me yksinkertaisesti soitamme, yhdistää kahden vektoritilan V ja W elementit, jotka osoittavat jokaisen vektorin v Kuuleminen yhdelle vektorille W - joka kuuluu W: lle tietyn operaation kautta.

Tämä muutos täyttää kaksi ehtoa:

Kuvio 1. Lineaarinen muunnos koskee vektoritilan V vektoria, jotta saadaan toinen vektoritilaan kuuluva vektori. Lähde: f. Zapata.

-Ehto 1

Se viittaa lisäykseen, joten t -lineaarinen muutos on täytettävä, että:

T (v + W -) = T (v) + T (W --A

-Ehto 2

Toinen ehto edustaa homogeenisuutta skalaarin kertolaskennassa vektorilla:

T (cv) = c⋅t (v-A

Lineaarinen muuntaminen, kuten nimestä päätetään.

Funktioiden merkintää käytetään myös lineaaristen muunnosten tapauksessa, joten V: n alue on muunnettava elementtien (vektorit) joukko, kun taas Codominium tai reitti on tuloksena oleva joukko.

Esimerkki lineaarisesta muutoksesta on:

Osoittaa, että kirjainta käytetään. Muutos sovelletaan vektoriin v joiden komponentit ovat x ja y, jota on esitetty yhdellä pylväällä matriisi. Tuloksena on toinen vektori W - jonka komponentit ovat x ja 0, edustavat myös pylväsmatriisia.

Siksi tämä on r -vektoritilan r muutos² Kohti vektoritilaa r², että yhteenvetona se on kirjoitettu näin:

T: r² → R²         

Jos meillä on vektori:

Muutos palauttaa meidät:

Ja niin millä tahansa vektorilla². Esimerkissä 1 varmistetaan, että tämä muunnos on lineaarinen.

[TOC]

Lineaaristen muunnosten ominaisuudet

Oletetaan, että V: n lineaarinen muuntaminen W: ssä, jossa vektorit v ja tai Ne kuuluvat V: hen, sitten seuraavat ominaisuudet täyttyvät:

Omaisuus 1

T (0 -) = 0 -

Missä 0 - Onko nollavektori.

Omaisuus 2

T (-v) = - t (v-A

Omaisuus 3

T (tai  - v) = T (tai) - t (v-A

Omaisuus 4

Olla v = c₁v₁ + c₂v₂ +.. . +  c_nv_n

 Niin:

T (c₁v₁ + c₂v₂ +.. . +  c_nv_n) = c₁ T (v₁) + c₂ T (v₂) +.. . +  c_n T (v_n-A

Lineaarisen muutoksen elementit

Olkoon v ja w jo mainittu vektoritilat, joissa lineaarinen muuntaminen t muuntavat V: n elementit W: ksi. Voimme määritellä seuraavat elementit:

-C -ydin tai ydin- Se on osa -alueesta, johon se merkitään N (t) jompikumpi ker (t) ja ymmärrä kaikki V: n elementit siten, että:

T (v) = 0 -.

Lineaarinen muunnos T (v) = 0 - kutsutaan nollamuutos.

Luonnollisesti nollavektori v = 0 - Täyttää joka tapauksessa tämän ehdon kanssa, mutta ydin koostuu koko ei -nollavektoreista, jotka myös täyttävät sen, tietylle T: lle.

Voi palvella sinua: Kasvava toiminto: Kuinka tunnistaa se, esimerkkejä, harjoituksia

-Kuva t- Se on W: lle kuuluvien vektorien joukko, joka on ainakin jonkin vektorin kuva V: ssä. Se on merkitty Im t) Ja se on W -vektoritilan osajoukko.

Nämä elementit auttavat meitä luokittelemaan lineaariset muunnokset myöhemmin.

Mitkä ovat lineaariset muunnokset?

Aluksi lineaariset muunnokset toimivat vektoritilojen kanssa, jotka on muodostettu vektoreilla. Monta kertaa yhdistämme vektorit vahvuuteen ja muihin fyysisiin voimakkuuksiin, mutta digitaalisen kuvankäsittelyssä pikseli voidaan edustaa vektorilla.

Tällöin kuvaa voidaan manipuloida kätevillä lineaarisilla muunnoksilla haluttujen vaikutusten saamiseksi, esimerkiksi projisoimalla, pyörivällä, peilikuvan löytämisellä tai sen kokoa muuttamatta suhteellisia ulottuvuuksia.

Lineaarisia muunnoksia käytetään myös laajasti taloudessa ja päätöksenteossa, esimerkiksi tietyn tuoteerän valmistukseen tarvittavan raaka -aineiden määrän tuntemiseksi.

Tehtaan tuottamien mallien koottamiseen tarvittavien kappaleiden lukumäärä voidaan työskennellä matriisijärjestelyn kautta, kuten myöhemmin näemme.

Lineaaristen muunnoksien tyypit (luokittelu)

Kuten toiminnot, lineaariset muunnokset voivat olla:

-Injektio tai monomorfismit

-Bijektiivit tai Epimorfismit

-Liiallinen tai Isomorfismit

Lisäksi seuraavat tyypit:

-Endomorfismit

-Automorfismit.

Injektiiviset lineaariset muunnokset

Olkoon v ja w vektoritilat ja t lineaarinen muunnos t: v → w. T on injektio, kun:

Kerma (T) = 0 -

Lineaariset ylin muunnokset

Jos v ja w ovat vektoritiloja siten, että t: v → w sanotaan, että T on bijektiivi, kun:

Im (t) = w

Bijjective Lineaarinen muunnokset

Lineaarinen muunnos T: V → W on bijektiivi, kun se on sekä injektio että ylihäiriö. Siksi on täyttynyt, että:

Kerma (T) = 0 - ja Im (t) = w

Endomorfismit

Ne ovat lineaarisia muunnoksia, joissa domeeni ja codominium osuvat.

Automorfismit

Tällaiset lineaariset muunnokset ovat bijektiivisia endomorfismeja.

Erityiset lineaariset muunnokset

Lineaarinen operaattori

Lineaarista muuntamista T: V → V, joka siirtyy vektoritilasta samaan vektoritilaan Lineaarinen operaattori.

Nollamuutos

Edellä mainittu, nollamuutos on tärkeä lineaarisen muunnoksen ytimen löytämiseksi:

Se voi palvella sinua: tetradecágon

T: V → W sellainen t (v) = 0 - Mille tahansa v.

Identiteetin muutos

T: V → V siten, että t (v) = v  Mille tahansa v.

Matriisin määrittelemä muunnos

T: V → W sellainen t (v) = Av, missä A on matriisi ja v Se on sarakevektori.

Lineaarinen toimenpide

Y = mx -tyypin lineaariset toiminnot ovat lineaarisia muunnoksia. Otetaan esimerkiksi y = 3x ja katso, vastaako se alun kaksi ehtoa, testata kahdella arvolla A ja B Any:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Todellakin se on lineaarinen muutos.

Sovellukset

Lineaarisilla muunnoksilla on matemaattisia sovelluksia, kuten:

-Koordinaattiakselien kierto.

-Lineaaristen differentiaaliyhtälöiden järjestelmien ratkaisussa.

-Itse -arvo- ja automaattiongelmat.

Ja heillä on myös sovelluksia muilla tieteenaloilla, esimerkiksi mekaniikassa, kvanttimekaniikassa ja taloudessa, muun muassa.

Esimerkkejä lineaarisista muunnoksista

Esimerkki 1

Monissa mekaniikan ongelmissa meidän on löydettävä vektorin projektio v Avaruuteen kuuluva, tietyllä tasolla. Tämä vektori v voi edustaa esimerkiksi voimaa.

Oletetaan, että haluat projisoida vektorin v = XY -tasolla. Voimme määritellä seuraavan matriisin antaman lineaarisen muunnoksen:

Kun käytämme sitä vektoriin v Saamme vektorin, jonka z -komponentti peruutetaan. Geometrisesti sitä on edustettuna v XY -tasolla punaisena vektorina, jossa on kaksi komponenttia.

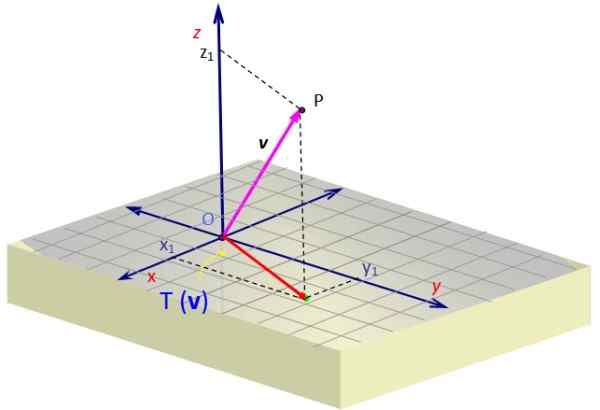Kuva 2. Vektorin projektio avaruudessa tasossa, joka saadaan lineaarisen muunnoksen kautta. Lähde: f. Zapata.

Esimerkki 2

Oletetaan

-Akselit tai pala

-Pyörät tai pala b

-Alusta tai pala c

Jokaiselle kärrytyypille kappaleiden lukumäärä on erilainen, koska mallit ovat erilaisia. Voimme sovittaa määrät 3 × 3 -matriisissa, jossa sarakkeet johtavat kärrytyyppi, ja riveät vastaavat kunkin mallin kehittämiseen tarvittavien kappaleiden määrää.

Tämä on esimerkki matriisin antamasta muutoksesta, joka olisi tällainen:

Jos tehdas saa tietyn ostotilauksen, joka koostuu x C1: n määrä, ja  c2 ja z -z C3: sta kuinka monta kappaletta A, B ja C on oltava käytettävissä tilauskärryn kokoamiseksi?

Se voi palvella sinua: mitkä ovat algebralliset lausekkeet ja jotka ovat yleisimpiä?

Meidän on löydettävä lineaarinen muunnos t (x) siten, että:

Saada vektori ja:

Se antaa meille osien määrän, jotka meillä on oltava käytettävissä. Vuoden aikana ratkaistu 2 arvioimme lineaaristen muunnosten tehokkuuden löytääksemme tietyn järjestyksen täyttämiseksi tarvittavien osien määrän.

Ratkaisut

- Harjoitus 1

Tarkista, että seuraava muunnos t: r² → R² Se on lineaarinen:

Ratkaisu

Tätä varten sinun on varmistettava, että muunnos täyttää kaksi alussa kuvattua ehtoa, ensin lisäys ja sitten skalaarin tuote vektorille. Joten sinun on otettava kaksi vektoria v ja  tai kuuluu r², Niiden kirjoittaminen matriisin merkinnällä tai komponenttien määrittämisellä.

Nämä vektorit ovat:

v = x₁, ja₁

tai = x₂, ja₂

Ensimmäinen kunto

-Muistaen, että vektorit on lisätty komponenttikomponentti, on varmistettava, että:

T (v+tai) = T (v) + T (tai-A

T (v+tai) = T (x₁+ x₂ ; ja₁ + ja₂-A

Täältä saadaan, että:

T (x₁+ x₂ ; ja₁ + ja₂) = (x₁+ x₂; 0)

-Toisaalta, kun levitetään muunnos jokaiseen vektoriin erikseen:

T (x₁,ja₁) + T (x₂,ja₂) = (x₁,0) + (x₂,0)

Lisäämällä tuloksena olevat vektorit, se saadaan tehokkaasti:

W - = (X₁+ x₂; 0)

Koska molemmat tulokset ovat identtisiä, ensimmäinen ehto täyttyy.

Toinen kunto

Nyt varmistamme, että kertomalla scler C: llä, se voi mennä pois muutoksesta:

T (cv) = c⋅t (v-A

Sean:

v = x₁, ja₁

c.v = C⋅x₁, C⋅y₁

Niin:

T (cv) = T (c⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0)

Mutta tiedämme, että edellisestä vaiheesta t (v) = T (x₁, ja₁ ) = (X₁ , 0).

Joten koska molemmat lausekkeet ovat identtisiä, toinen tila täyttyy myös ja muunnos on lineaarinen.

- Harjoitus 2

Lelukorin tehdas kokoaa kolme ajoneuvomallia: C1, C2 ja C3, joille tarvitset kappaleita A, B ja C, jotka ovat vastaavasti akselit, pyörät ja alustat. Vaadittavat määrät ovat seuraavassa taulukossa:

Tehdasta on pyydetty valmistamaan 12 mallia C1, 22 C2 ja 16 C3. Kuinka monta kappaletta A, B ja C on tilauksen suorittamiseksi?

Ratkaisu

Lineaarinen muunnos t (x) = y sovelletaan, jonka tulos on matriisien välinen tuote:

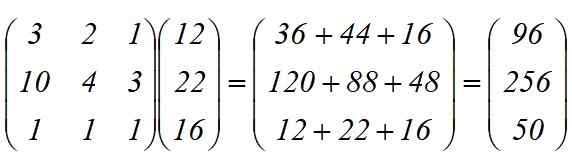
Niitä vaaditaan yhteensä:

-96 akselia

-256 pyörää

-50 runko.

Viitteet

1. Algebra ja analyyttinen geometria. Ydin ja kuva. Lineaaristen muunnosten luokittelu. Toipunut: Aga.frba.Utn.Edu.AR.
2. Grossman, S. 2012. Lineaarialgebra. Seitsemäs. Painos. McGraw Hill.
3. Gutiérrez, E. 2014. Lineaarinen algebra ja sen sovellukset. Patria -toimitusryhmä.
4. Larson, r. 2016. Lineaarisen algebran perusteet. Kuudes. Painos. Cengage -oppiminen.
5. Wikipedia. Lineaariset sovellukset. Palautettu: on.Wikipedia.org.