Fourier Diskreet Transformated -ominaisuudet, sovellukset, esimerkit

Se Fourier Diskreet Transformat Se on numeerinen menetelmä, jota käytetään signaalin muodostavien spektritaajuuksiin liittyvien näytteiden määrittelemiseen. Tutki säännöllisiä funktioita suljetuissa parametreissa, heittäminen seurauksena toinen hienovarainen signaali.

Furierin huomaamaton muunnos N -pisteistä, hienovaraisella signaalilla, seuraavat 2 olosuhdetta sekvenssissä on täytettävä X [n]

 x [n] = 0   N n - 1

Näiden olosuhteiden täyttämisessä Fourierin erillinen muunnos voidaan määritellä

TDF

Fourierin huomaamaton muunnos voidaan määritellä näytteenotoksi Fourier -muunnoksen N -pisteissä.

[TOC]

Fourierin huomaamaton muunnos tulkinta

Lähde: Pexels

On 2 näkökulmaa, joista sekvenssillä X saadut tulokset voidaan tulkita_s[n] Fourierin hienovaraisen muunnoksen kautta.

-Ensimmäinen vastaa spektrikertoimia, Fourier -sarjan jo tunnetut. Sitä havaitaan erillisissä jaksollisissa signaaleissa, näytteillä samaan aikaan sekvenssin X kanssa_s[N].

-Toinen on suunnilleen hienovaraisen aperiadisen signaalin spektriä, näytteitä, jotka vastaavat sekvenssiä x_s[N].

Diskreet -muunnos on lähestymistapa alkuperäisen analogisen signaalin spektriin. Sen vaihe riippuu näytteenottohetkistä, kun taas sen suuruus riippuu näytteenottovälistä.

Ominaisuudet

Rakenteen algebralliset perusteet muodostavat seuraavien osien loogisen perustan.

Lineaarisuus

C . S_n → C . F [S_{k -k -}] Jos sekvenssi kerrotaan skalaarilla, sen muuntaminen on myös.

T_n + V_n = F [t_{k -k -}]+F [v_{k -k -}] Summan muunnos on yhtä suuri kuin muunnettujen summa.

Kaksinaisuus

F [s_n] → (1/n) s_-K; Jos Fourierin hienovarainen muunnos palautetaan jo transformoituneeksi lausekkeelle, sama lauseke saadaan, kiipeäminen N: n käänteessä pystysuoraan akseliin nähden.

Konvoluutio

Jahtaamalla samanlaisia ​​tavoitteita, jotka Laplace -muunnossa toimintojen konvoluutio viittaa tuotteeseen sen Fourier -muunnosten joukossa. Konvoluutio koskee myös erillisiä aikoja ja vastaa monista nykyaikaisista menettelyistä.

X_n * R_n → F [x_n- .F [r_n] Konvoluution muuntaminen on yhtä suuri kuin muutettujen tuote.

X_n . R -_n→ F [x_n] * F [r_n] Tuotteen muuntaminen on yhtä suuri kuin muunnettujen konvoluutio.

Siirtymä

X_N-m → F [x_{k -k -}] e ^{-I (2π/n) km} ; Jos peräkkäisyys viivästyy M -näytteissä, sen vaikutus diskreettiseen muunnokseen on modifikaatio (2π/n) km: n määrittelemän kulman modifikaatio.

Voi palvella sinua: Miksi algebra on tärkeä tietyissä päivittäisessä tilanteessa?

Symmetria konjugoitu

X_t [-K] = x*_t[k] = x_t [N - k]

Modulaatio

W -^-nm_N . x [n] ↔ x_t[K - m]

Tuote

x [n] y [n] ↔ (1/n) x_t[k]*ja_t[K]

Symmetria

X [-n] ↔ x_t[-K] = x*_t[K]

Konjugoida

x*[n] ↔ x*_t[-K]

Jäsenyhtälö 

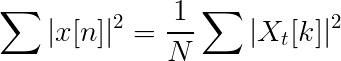
Yhtäläisyydet ja erot Fourier -muunnoksen kanssa

Fourierin tavanomaisen muunnoksen suhteen sillä on useita yhtäläisyyksiä ja eroja. Fourierin muunnos muuntaa sekvenssin jatkuvaksi viivaksi. Tällä tavoin sanotaan, että Fourier -muuttujan tulos on monimutkainen todellisen muuttujan funktio.

Fourierin hienovarainen muunnos, toisin kuin, vastaanottaa hienovaraisen signaalin ja muuttaa sen toiseksi hienovaraiseksi merkiksi, ts. Sekvenssi.

Mikä on Fourierin huomaamaton muunnos?

Ne toimivat pääasiassa merkittäviä yhtälöitä, kun taas voimaelementeiksi johdetut lausekkeet muuttavat. Eroaineiden merkitseminen integroitavien polynomien muodoissa.

Tulosten optimoinnissa, moduloinnissa ja mallintamisessa se toimii standardisoiduna lausekkeena, joka on usein tekniikan resurssi useiden sukupolvien jälkeen.

Lähde: Pixabay

Historia

Tämän matemaattisen konseptin esitteli Joseph B. Fourier vuonna 1811 kehitettäessä sopimusta Lämmön leviäminen. Se ottivat sen nopeasti käyttöön eri tieteen ja tekniikan sivukonttorit.

Se perustettiin päätyökaluna tutkiessaan yhtälöitä osittaisten johdannaisten kanssa, vertaamalla jopa työsuhteita Laplace Transformated ja tavalliset differentiaaliyhtälöt.

Mikä tahansa funktio, jota voidaan työskennellä Fourier -muunnoksen kanssa, on oltava mitätöisyys määritetyn parametrin ulkopuolella.

Fourier Diskreet Transformed ja sen käänteinen

Diskreet -muunnos saadaan lausekkeen kautta:

Diskreet -sekvenssin x jälkeen [n]

Fourierin huomaamaton muunnos on määritelty lausekkeen kautta:

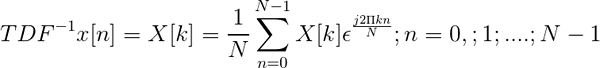Käänteinen TDF

Se sallii, kun diskreet on muunnettu, määritä sekvenssi aikadomeenissa x [n].

Hienoudet

Fourierin erillistä muunnosta vastaava parametrointiprosessi on pentussa. Muutoksen suorittamiseksi meidän on rajoitettava sekvenssi ajoissa. Monissa tapauksissa kyseisillä signaaleilla ei ole näitä rajoituksia.

Peräkkäinen, joka ei täytä kokikriteerejä, joita voidaan soveltaa huomaamattomaan muunnokseen, voidaan kertoa ”ikkuna” V [n] -funktiolla, määrittelemällä peräkkäin käyttäytyminen ohjattavassa parametrissa.

Voi palvella sinua: Pyöreät permutaatiot: esittely, esimerkit, ratkaistu harjoitus

X [n] . V [n]

Spektrin leveys riippuu ikkunan leveydestä. Kun ikkunan leveys kasvaa, laskettu muutettu on kapeampi.

Sovellukset

Perusratkaisun laskeminen

Fourier's Diskreet Transform on tehokas työkalu erillisten peräkkäisten tutkimusten tutkimuksessa.

Fourierin huomaamaton muunnos muuttaa jatkuvan muuttujan funktion, erillisen muuttujan muunnokseksi.

Cauchyn lämpöyhtälön ongelma esittelee usein Fourierin huomaamattoman muunnoksen käyttökentän. Missä funktio syntyy Dirichlet -lämpö tai ydin ydin, joka koskee arvoja, jotka näytteenotto on määritelty parametri.

Signaaliteoria

Yleinen syy Fourierin erillisen muunnoksen soveltamiseen tässä haarassa johtuu lähinnä signaalin ominaishajoamisesta äärettömänä päällekkäisyytenä helpommin hoidettavien signaalien kanssa.

Se voi olla ääniaalto tai sähkömagneettinen aalto, Fourierin erillinen muunnos ilmaisee sen yksinkertaisessa aaltossa. Tämä esitys on melko usein sähkötekniikassa.

Fourierin sarja

Ne ovat määriteltyjä sarjoja kosenosten ja rintojen suhteen. Ne auttavat helpottamaan työtä yleisten jaksollisten toimintojen kanssa. Sovellettuna ne ovat osa osittaisten ja tavallisten differentiaaliyhtälöiden resoluutiotekniikoita.

Fourier -sarja on vielä yleisempi kuin Taylorin sarja, koska ne kehittävät jaksollisia disontinua -funktioita, joilla ei ole esitystä Taylor -sarjassa.

Fourier -sarjan muut muodot

Analyyttisesti Fourierin muunnos on tärkeää.

-Fourier -sarja 2L -jakson toiminnolla:

Monta kertaa on tarpeen mukauttaa Fourier-sarjan rakenne, jaksollisiin toimintoihin, joiden ajanjakso on p = 2L> 0 aikavälillä [-l, l].

-Fourier -sarja tasaisina ja parittomissa toiminnoissa

Aika [-π, π] otetaan huomioon, joka tarjoaa etuja funktioiden symmetristen ominaisuuksien hyväksi.

Voi palvella sinua: äärellinen sarja: Ominaisuudet, esimerkit, ratkaisut harjoitukset

Jos F on vääntömomentti, Fourier -sarja on perustettu sarjanaan Cosenos.

Jos F on outoa, Fourier -sarja on perustettu rintojen sarjana.

-Fourier -sarjan monimutkainen merkintä

Jos sinulla on f (t) -toiminto, joka täyttää kaikki Fourier-sarjan vaatimukset, on mahdollista merkitä se aikavälillä [-t, t] sen monimutkaisen merkinnän avulla: 

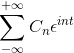
Esimerkit

Perusratkaisun laskemisesta esitetään seuraavat esimerkit:

Laplace -yhtälö

Lämpöyhtälö

Schrödinger -yhtälö

Aaltoyhtälö

Toisaalta on esimerkkejä Fourierin erillisen muunnoksen soveltamisesta signaaliteorian alaan:

-Järjestelmän tunnistusongelmat. Perustettu f ja g

-Ongelma lähtösignaalin johdonmukaisuudessa

-Ongelmat signaalin suodatuksessa

Harjoitukset

Harjoitus 1

Laske Fourierin huomaamaton muunnos seuraavalle peräkkäiselle.

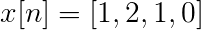
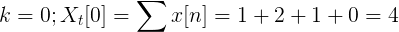
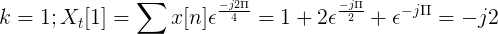
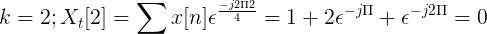
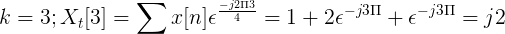
X [n] TDF voidaan määritellä seuraavasti:

X_t[k] = 4, -j2, 0, j2 K = 0, 1, 2, 3

Harjoitus 2

Digitaalisen algoritmin kautta halutaan määrittää lausekkeella x (t) = e määrittelemä spektrisignaali^-t. Jos kertoimen enimmäistaajuus on f_m= 1Hz. Harmoninen vastaa F = 0.3 Hz. Virhe on rajoitettu alle 5%: iin. Laskea F_s , D ja n.

Ottaen huomioon näytteenottolause F_s = 2f_m = 2 Hz

Taajuuden resoluutio F_{0 -} = 0.1 Hz, missä saadaan d = 1/0,1 = 10 s

0 -.3 Hz on indeksia K = 3 vastaava taajuus, missä n = 3 × 8 = 24 näytettä. Osoittaa sen F_s = N/d = 24/10 = 2.4> 2

Koska tarkoituksena on saavuttaa N: n mahdollinen arvo n, seuraavia arvoja voidaan pitää ratkaisuna:

F_{0 -} = 0.3 Hz

D = 1/0.3 = 3.33S

K = 1

N = 1 × 8 = 8

Viitteet

1. Diskreetin Fourier -muunnoksen hallitseminen yhdessä, kahdessa tai useammassa ulottuvuudessa: sudenkuopat ja esineet. Isaac. Springer Science & Business Media, 19. heinäkuuta. 2013
2. DFT: Omistajien käsikirja erilliselle Fourier -muunnolle. William L. Briggs, Van Emden Henson. SIAM, 1. tammikuuta. tuhatyhdeksänsataayhdeksänkymmentäviisi
3. Digitaalinen signaalinkäsittely: teoria ja käytäntö. D -d. Sundararajan. World Scientific, 2003
4. Muunnokset ja nopeat algoritmit signaalianalyysiä ja esityksiä varten. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6. joulukuuta. 2012
5. Diskreetti ja jatkuvat Fourier -muunnokset: analyysi, sovellukset ja nopeat algoritmit. Eleanor Chu. CRC Press, 19. 2008