Escaleno trapezio -ominaisuudet, kaavat ja yhtälöt, esimerkkejä

Eräs trapetsi skaaleeni Se on neljä -puolta monikulmio, joista kaksi on yhdensuuntainen toistensa kanssa ja sen neljällä sisäkulmalla eri mitat.

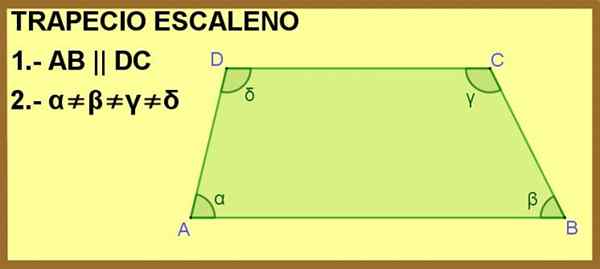
ABCD -kvadrilateraali on esitetty, missä sivut AB ja DC ovat yhdensuuntaisia ​​toistensa kanssa. Tämän kanssa riittää tekemään siitä trapetsin, mutta lisäksi a-, β-, y- ja Δ -sisäkulmat ovat kaikki erilaisia, joten trapetsoidi on escalano.

Kuvio 1. ABCD -kvadrilateraali on trapetsi tilalle 1 ja Scalene Edellylle 2. Lähde: f. Zapata.

[TOC]

Scaleno -tarttumisen elementit

Tyypillisimpien elementtien alapuolella:

-Tukikohdat ja puoli: Trapetsin yhdensuuntaiset sivut ovat sen emäkset ja kaksi ei -rinnakkaista sivua ovat sivut.

Scaleen -trapeziossa emäkset ovat eripituisia ja myös sivut. Skaaleenijärjestelmän trapetsoidilla voi kuitenkin olla yhtä pitkä puoli kuin pohja.

-Mediaani: Segmentti liittyy sivujen keskipisteisiin.

-Diagonaali: Trapetsin diagonaali on segmentti, joka liittyy kahteen vastakkaiseen kärkeen. Trapetsissa, kuten jokaisessa kvadrilateraalisessa, on kaksi diagonaalia. Scalene trapeziossa ne ovat eripituisia.

Muut trapezoidit

Escaleno trapezion lisäksi on muitakin erityisiä trapetsoideja: suorakulmio trapezoidi ja šosceles trapezoidi.

Trapetsi on suorakulmio, kun yksi sen kulmista on suora, kun taas Trapezio -tasapelin sivut ovat yhtä pituisia.

Trapetsoidisessa muodossa on lukuisia sovelluksia suunnittelu- ja teollisuustasolla, kuten lentokoneiden siipien kokoonpanossa, jokapäiväisten esineiden, kuten taulukoiden, tuolien varmuuskopioiden, muodossa.

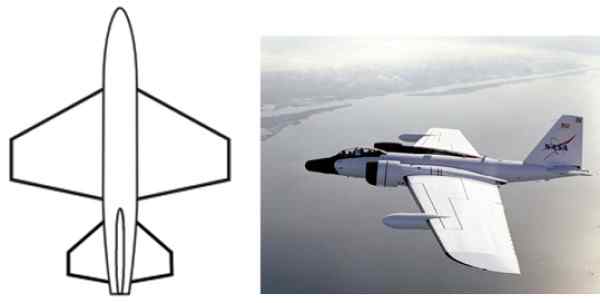Kuva 2. Trapetsoidinen muoto on yleinen Alar -lentokoneiden kokoonpanossa. Lähde: Wikimedia Commons.

Ominaisuudet

Seuraavaksi luetellaan kiipeilymallin ominaisuudet, joista monet ovat laajoja muun tyyppisiä trapezoideja. Seuraavassa.

1. Trapezoidin mediaani, toisin sanoen segmentti, joka yhdistää sen ei -rinnakkaiset puolet, on yhdensuuntainen minkä tahansa emäksen kanssa.

2.- Trapezoidin mediaanilla on pituus, joka on sen emäksen puoliksi ja leikkaa diagonaalit keskipisteessä.

3.- Trapetsin diagonaalit leikkaavat pisteeseen, joka jakaa ne kahteen osaan, jotka ovat verrannollisia emäksen suhteeseen.

4.- Trapetsin diagonaalien neliöiden summa on yhtä suuri kuin sen sivujen neliöiden summa sekä sen emäksen kaksoistuote.

5.- Keski -diagonaalipisteisiin liittyvä segmentti on pituus, joka on yhtä suuri kuin emäksen puolivälissä.

Voi palvella sinua: injektiotoiminto: mistä se koostuu, mihin se on ja esimerkkejä

6.- Sivujen vieressä olevat kulmat ovat täydentäviä.

7.- Skaaleneissa trapetsissa sen diagonaalien pituus on erilainen.

8.- Trapetsissa on rekisteröity keho vain, jos sen emäksen summa on yhtä suuri kuin sen sivujen summa.

9.- Jos trapetsissa on rekisteröity kehä, niin kulma, jossa kärjessä on mainitun ympärysmitta ja sivut, jotka kulkevat trapetsin sivuttaispään läpi, on suora.

10.- Escaleno -trapetsissa ei ole rajoitettua kehä, ainoa trapetsin tyyppi.

Kaavat ja yhtälöt

Seuraavat kiipeily -trapetsin suhteet viitataan seuraavaan lukuun.

1.- Jos ae = ed ja bf = fc → ef || AB ja EF || DC.

2.- Ef = (ab + dc)/2 eli: m = (a + c)/2.

3.- Di = ib = d₁ /2 ja AG = GC = D₂ /2.

4.- Dj / jb = (c / a) vastaavasti cj / ja = (c / a).

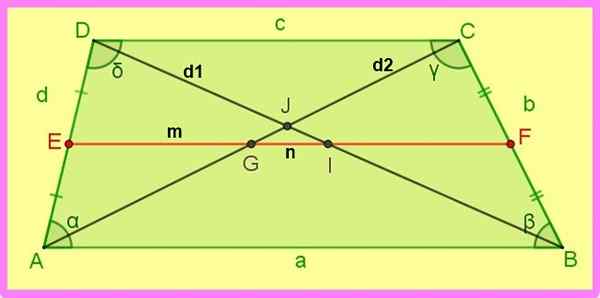Kuva 3. Saleeni -trapetsoidin mediaani ja diagonaalit. Lähde: f. Zapata.

5.- Db² + Ac² = Mainos² + BC² + 2 AB ∙ DC 

Vastaavasti:

d -d₁² + d -d₂² = D² + b -² + 2 A ∙ C

6.- GI = (AB - DC)/2

Tarkoittaen:

n = (a - c)/2

7.- α + Δ = 180⁰ ja β + γ = 180⁰

8.- Jos α ≠ β ≠ γ ≠ δ, niin D1 ≠ D2.

9.- Kuvio 4 esittää Scaleen -trapetsoidia, jolla on rekisteröity keho, siinä tapauksessa on täytettävä, että:

A + c = d + b

10.- Myös ABCD: n escalene -trapetsoidi, jossa on rekisteröity keskuksen keskusta tai seuraava on toteutettu:

∡Aod = ∡boc = 90⁰

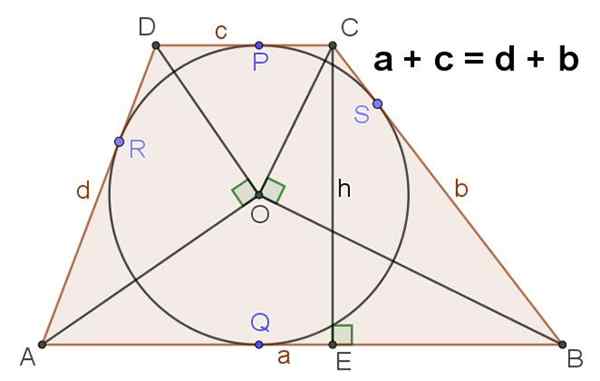Kuva 4. Jos trapetsissa varmistetaan, että sen emäksen summa on yhtä suuri kuin sivujen summa, niin samaan on kirjoitettu kehä. Lähde: f. Zapata.

Korkeus

Trapetsin korkeus määritellään segmentiksi, joka siirtyy pohjan pisteestä kohtisuorassa vastakkaiseen pohjaan (tai sen laajennukseen).

Kaikilla trapetsin korkeuksilla on sama mitta h, joten suurimman osan ajasta sanan korkeus viittaa sen mittaukseen. Lyhyesti sanottuna, korkeus on emäksen etäisyys tai erotus.

Korkeus H voidaan määrittää, tiedetäänkö sivu sivun pituus ja yksi sivun vieressä olevista kulmista:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (Δ)

Mediaani

Trapezoidin M -mediaani mitta on emäksen puolikehykset:

M = (a + b)/2

Diagonaalit

d -d₁ = √ [a² + d -d² - 2 ∙ a ∙ d ∙ cos (α)]

d -d₂= √ [a² + b -² - 2 ∙ A ∙ B ∙ COS (β)]

Se voidaan myös laskea, jos vain trapetsoidin pituus tunnetaan:

d -d₁ = √ [b² + A ∙ C - A (B² - d -d²)/(a - c)]

d -d₂ = √ [D² + A ∙ C - A (D² - b -²)/(a - c)]

Kehä

Ympäristö on ääriviivan kokonaispituus, ts. Kaikkien sivujen summa:

Voi palvella sinua: Diskreetti satunnaismuuttuja

P = a + b + c + d

Alue

Trapezoidin pinta -ala on sen emäksen puolivälissä kerrottuna sen korkeudella:

A = h ∙ (a + b)/2

Se voidaan myös laskea, jos mediaani M ja korkeus tiedetään:

A = m ∙ h

Jos vain trapetsoidien puolten pituus tunnetaan, alue voidaan määrittää Herónin kaavalla trapetsoidille:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]]]

Missä s on puolijohde: s = (a+b+c+d)/2.

Muut kiipeilyn suhteet

Mediaani diagonaalien ja diagonaalien risteyksen läpi kulkevan rinnakkaisleikkaus aiheuttaa muita suhteita.

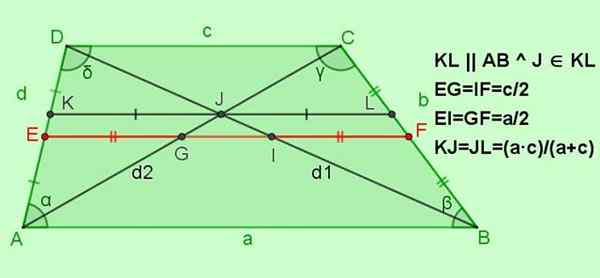Kuva 5. Muut kiipeilyn suhteet. Lähde: f. Zapata.

-Suhteet mediaaniin EF

Ef = (a+c)/2; Esim. = If = c/2; Ei = gf = a/2

-Rinnakkaissegmentin suhteet KL -emäksille ja se kulkee pisteen läpi Diagonaalien risteys J

Kyllä KL || AB || DC j ∈ Kl, sitten kj = jl = (a ∙ c)/(a+c)

Scaleen -trapeziumin rakentaminen sääntöllä ja kompassilla

Kun otetaan huomioon pituudet -lla ja c, Olla A> c ja pituuden B ja d -d, olemus b> d, Jatkamme näitä vaiheita (katso kuva 6):

1.- Säännöllä vedetään suurimman AB: n segmentti.

2.- SE: stä ja AB: stä, kohta P on merkitty siten, että AP = C.

3.- Kompassin kanssa C- ja Radio D -keskuksessa piirretään kaari.

4.- Se tehdään B: ssä B: ssä radiossa B piirtää kaaria, joka tulkitsee edellisessä vaiheessa laadun kaaren. Kutsumme risteyspisteeksi.

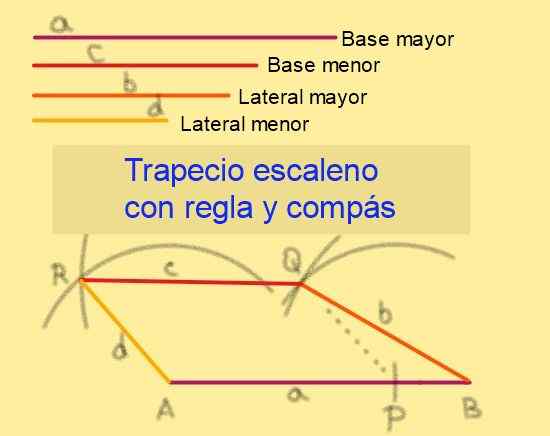Kuva 6. Escaleno Trapecion rakentaminen sen sivuille. Lähde: f. Zapata.

5.- Keskustan piirtämisessä sädekaari D.

6.- Keskustaan, jossa voidaan piirtää sädekaari, joka sieppasi edellisessä vaiheessa laadittuun kaariin. Sitä kutsutaan r leikkauspisteeseen.

7.- Segmentit BQ, QR ja RA vedetään säännön kanssa.

8.- ABQR -kvadrilateriaali on skaalenien trapetsoidi, koska APQR on rinnakkaisohjelma, joka takaa, että AB || Qr.

Esimerkki

Seuraavat pituudet on annettu CM: llä: 7, 3, 4 ja 6.

a) Määritä, voivatko heidän kanssaan rakentaa skaalene -trapetsin, joka voi ratkaista ympärysmitta.

b) Löydä kehä, alue, diagonaalien pituus ja mainitun trapetsin korkeus sekä rekisteröidyn kehän säde.

- Liittää jhk

Käyttämällä pituisia 7 ja 3 -segmenttejä emäksinä ja sivuina pituudeltaan 4 ja 6, skaaleeni trapetsoidi voidaan rakentaa käyttämällä edellisessä osassa kuvattua menettelyä.

Meidän on tarkistettava, onko siinä rekisteröity kehys, mutta omaisuuden muistaminen (9):

Voi palvella sinua: kuusikulmainen prisma

Trapetsissa on rekisteröity keho vain, jos sen emäksen summa on yhtä suuri kuin sen sivujen summa.

Näemme sen todella:

7 + 3 = 4 + 6 = 10

Sitten kirjoitetun ympärysmitta täyttyy.

- Ratkaisu b

Kehä

Kehä P saadaan lisäämällä sivut. Koska tukikohdat ovat yhteensä 10 ja myös sivut, kehä on:

P = 20 cm

Alue

Alueen määrittämiseksi, vain sen sivut, suhde sovelletaan:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]]]

Missä S on puolijohde:

S = (a+b+c+d)/2.

Meidän tapauksessamme puolijohde on S = 10 cm: n arvoinen. Kun vastaavat arvot vaihdetaan:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

On jäljellä:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Korkeus

Korkeus H liittyy alueelle A seuraavan lausekkeen kautta:

A = (a+c) ∙ h/2, missä korkeus voidaan saada puhdistuksella:

H = 2a / (a+c) = 2 * 19,84 / 10 = 3,968 cm.

Rekisteröity kehysradio

Rekisteröityn kehän säde on puolet korkeudesta:

R = h/2 = 1 984 cm

Diagonaalit

Lopuksi diagonaalien pituus:

d -d₁ = √ [b² + A ∙ C - A (B² - d -d²)/(a - c)]

d -d₂ = √ [D² + A ∙ C - A (D² - b -²)/(a - c)]

Arvojen asianmukainen korvaaminen on:

d -d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

d -d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

Eli: D₁ = 4,69 cm ja D₂ = 8,49 cm

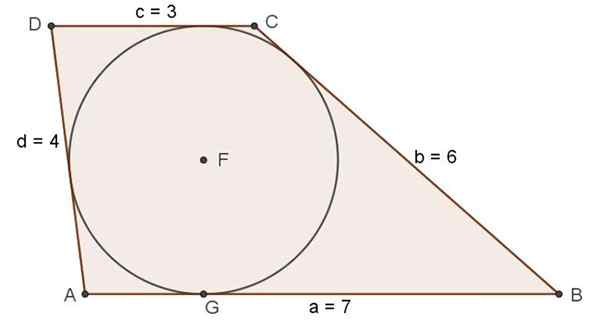Kuva 7. Scalene trapezio, joka täyttää rekisteröidyn ympärysmittaisen olemassaolon tilanteen. Lähde: f. Zapata.

Liikuntaa

Määritä trapezoidia ab = a = 7, cd = c = 3 ja lateraalinen BC = b = 6, da = d = 4.

Ratkaisu

Kosinin lause voidaan käyttää kulmien määrittämiseen. Esimerkiksi kulma ∠A = α määritetään kolmiosta ABD: llä AB = A = 7, BD = D2 = 8,49 ja DA = D = 4.

Tähän kolmioon sovellettu kosininlause pysyy näin:

d -d₂² = a² + d -d² - 2 ∙ a ∙ d ∙ cos (α), eli:

72 = 49+16-56 ∙ cos (α).

Kun puhdistetaan, saadaan kulman α kosini:

Cos (α) = -1/8

Toisin sanoen α = arccos (-1/8) = 97,18⁰.

Samoin muut kulmat saadaan, niiden arvot ovat:

β = 41,41⁰; γ = 138,59⁰ ja lopulta Δ = 82,82⁰.

Viitteet

1. C. JA. -Lla. (2003). Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Campos, f., Cerecedo, f. J -. (2014). Matematiikka 2. Patria -toimitusryhmä.
3. Vapautettu, k. (2007). Tutustu monikulmioihin. Vertailuindeksiyhtiö.
4. Hendrik, V. (2013). Yleiset monikulmiot. Birkhäuser.
5. Iger. (S.F.-A. Matematiikka ensimmäisen lukukauden Tacaná. Iger.
6. Jr. Geometria. (2014). Monikulmio. Lulu Press, Inc.
7. Miller, Heeren ja Hornsby. (2006). Matematiikka: Perustelu ja sovellukset (kymmenes painos). Pearson -koulutus.
8. Patiño, m. (2006). Matematiikka 5. Toimitusohjelma.
9. Wikipedia. Trapetsi. Palautettu: on.Wikipedia.com