Trececio -ivasceles -ominaisuudet, suhteet ja kaavat, esimerkit

Eräs trapetsi sammutus Se on nelinkertainen.

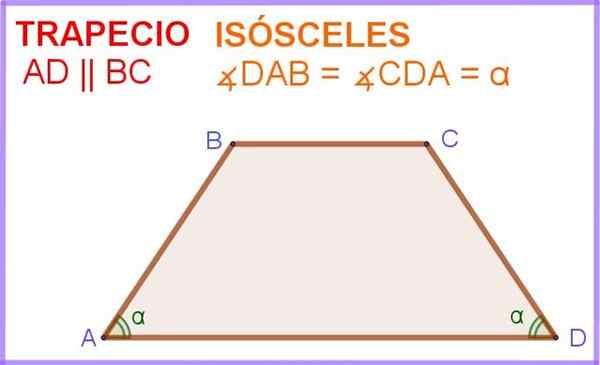
Kuvassa 1 sinulla on ABCD -nelikulmainen, jossa AD- ja BC -sivut ovat yhdensuuntaiset. Lisäksi kulmilla ∠DAB: lla ja ∠ADC: llä rinnakkaispuolen AD: n vieressä on sama mitta α. 

Kuvio 1. Trapezium -sammutus. Lähde: f. Zapata.

Siten tämä kvadrilateraalinen tai neljä puolella olevaa monikulmiota on käytännössä samanakasta trapetsoidi.

Trapetsissa rinnakkaisia ​​sivuja kutsutaan pohjat ja ei-selkäyksiä kutsutaan sivuttais-. Toinen tärkeä ominaisuus on korkeus, mikä on etäisyys, joka erottaa yhdensuuntaiset sivut.

Trapetsoidien lisäksi on muun tyyppistä trapetsia:

-TRapecio escaleno, Sillä on kaikki sen eri kulmat ja sivut.

-TSuorakulmio, jossa sivulla on suorat viereiset kulmat.

Trapetsoidinen muoto on yleinen suunnittelun, arkkitehtuurin, elektroniikan, laskelman ja monien muiden eri alueilla, kuten myöhemmin nähdään. Siksi sen ominaisuuksien tuntemisen tärkeys.

[TOC]

Ominaisuudet

Yksinoikeudella sijaitsevat šosceles trapezoid

Jos trapetsia on samasosaa, vastaa seuraavat ominaisominaisuudet:

1.- Sivuilla on sama mitta.

2.- Pohjojen vieressä olevat kulmat ovat samat.

3.- Vastakkaiset kulmat ovat täydentäviä.

4.- Diagonaaleilla on sama pituus, sama ovat kaksi segmenttiä, jotka yhdistävät vastakkaiset kärkipisteet.

5.- Pohjojen ja diagonaalien välinen kulma on kaikki sama mitta.

6.- Se on rajoittanut ympärysmitta.

Vastavuoroisesti, jos trapetsi täyttää jokin aikaisemmista ominaisuuksista, se on šosceles trapezoidi.

Jos trapezoidissa tasapainoissa yksi kulmista on suora (90º), niin kaikki muut kulmat ovat myös suorakulmion muodostaminen. Toisin sanoen suorakulmio on erityinen tapauskohtaista trapezoidia.

Kuva 2. Corn Palomites -säiliö ja koulupöydät ovat muotoiltuja samanaikaisesti. Lähde: PxFuel (vasen)/McDowell Craig Flickrin kautta. (Oikea)

Kaikille trapezoidille

Seuraava ominaisuusjoukko on voimassa mihin tahansa trapetsiin:

7.- Se mediaani Trapetsista, joka on segmentti, joka liittyy sen ei -rinnakkaisten sivujen keskipisteisiin, on yhdensuuntainen minkä tahansa emäksen kanssa.

8.- Mediaanin pituus on yhtä suuri kuin sen emäksen pituus (summa 2).

9.- Trapezoidin mediaani leikkaa diagonaalit keskipisteessä.

10.- Trapetsin diagonaalit leikkaavat pisteeseen, joka jakaa ne kahteen osaan, jotka ovat verrannollisia emäksen osuuteen.

yksitoista.- Trapetsin diagonaalien neliöiden summa on yhtä suuri kuin sen sivujen neliöiden summa sekä sen emäksen kaksoistuote.

Se voi palvella sinua: kuinka monta tuhannesa he sopivat kymmenesosaan?

12.- Keski -diagonaalipisteisiin liittyvä segmentti on pituus, joka on yhtä suuri kuin emäksen puolivälissä.

13.- Sivujen vieressä olevat kulmat ovat täydentäviä.

14.- Trapetsissa on rekisteröity kehä, jos ja vain jos sen emäksen summa on yhtä suuri kuin sen sivujen summa.

viisitoista.- Jos trapetsissa on rekisteröity kehä, niin kulmat, joiden kärkipiste on mainitun kehän keskellä ja saman puolen päät kulkevat sivut, ovat suorat kulmat.

Suhteet ja kaavat

Seuraavat suhteet ja kaavat viitataan kuvioon 3, jossa samasosien lisäksi trapezoidit muut jo mainitut tärkeät segmentit, kuten diagonaalit, korkeus ja väliaine.

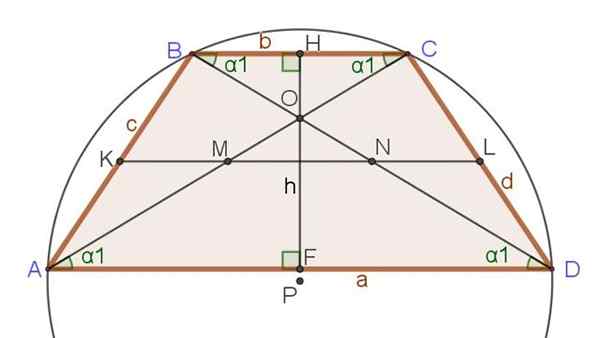Kuva 3. Mediaani, diagonaalit, korkeus ja kehä. Lähde: f. Zapata.

Eksceles Trapecio -suhteet

1.- AB = DC = C = D

2.- ∡DAB = ∡CDA ja ∡ABC = ∡BCD

3.- ∡DAB + ∡BCD = 180º ja ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α₁

6.- A, B, C ja D kuuluvat rajoitettuun ympärysmitta.

Minkä tahansa trapezoidin suhteet

7. Jos AK = KB ja DL = LC ⇒ KL || AD ja KL || BC

8.- Kl = (ad + bc)/2

9.- Am = mc = ac/2 ja dn = nb = db/2

10.- AO/OC = ad/bc y do/ob = ad/bc

yksitoista.- Ac² + Db² = AB² + DC² + 2⋅ad⋅BC

12.- Mn = (ad - bc)/2

13.- ∡DAB + ∡ABC = 180º ja ∡CDA + ∡BCD = 180º

14.- Jos AD + BC = AB + DC ⇒ ∃ R Mikä AD: n, BC, AB ja DC

viisitoista.- Jos ∃ r mikä ad, BC, AB ja DC, niin: niin:

∡bra = ∡drc = 90º

Iskosceles Trapezoid -suhteet rekisteröityyn ympärysmittaan

Jos šosceles trapezoid.

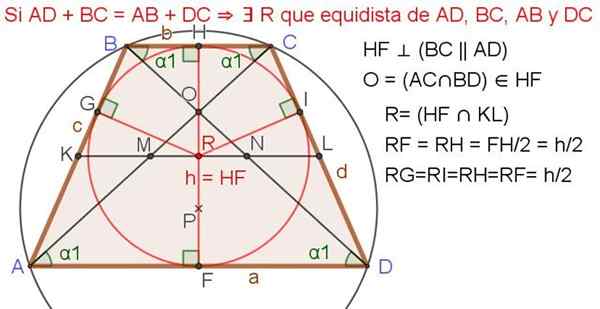Kuva 4. Trapetsia rekisteröidyllä kehällä. Lähde: f. Zapata.

Seuraavat ominaisuudet sovelletaan, kun tasavirheiden trapetsoidilla on rekisteröity kehä (katso kuva 4 yllä):

16.- Kl = ab = DC = (ad + bc)/2

17.- Diagonaalit leikataan suorassa kulmassa: AC ⊥ BD

18.- Korkeus on sama kuin mediaani: hf = kl, eli h = m.

19.- Korkeuden neliö on yhtä suuri kuin emäksen tuote: H² = Bc⋅ad

kaksikymmentä.- Näissä erityisissä olosuhteissa trapetsialue on yhtä suuri kuin emäksen korkeuden tai tuote: pinta -ala = h² = Bc⋅ad.

Kaavat toisen puolen määrittämiseksi, toiset ja kulma

Tunnettu yksi pohja, sivu ja kulma, toinen pohja voidaan määrittää:

a = b + 2c cos α

B = a - 2c cos α

Jos emäksen pituus tunnetaan tiedossa ja kulma, molempien puolten pituudet ovat:

Se voi palvella sinua: Fermat -raja: mikä koostuu ja harjoitukset ratkaistu

C = (a - b) / (2 cos α)

Päättäväisyys toisella puolella, tunnet muut ja diagonaali

A = (D₁² - c²)/ B;

B = (d₁² - c²)/ 

C = √ (D₁² - A⋅b)

Missä D₁ Se on diagonaalien pituus.

Pohja korkeudesta, alueesta ja toisesta pohjasta

a = (2 a)/h - b

b = (2 a)/h - a

Tunnetaan tukikohdat, alue ja kulma

C = (2a) /[(a + b) sin α]

Tunnetaan sivuttainen mediaani, alue ja kulma

C = a / (m.synti α)

Tunnettu korkeus sivut

H = √ [4 c² - (A - b)²-

Tunnettu korkeus kulma ja kaksi puolta

H = tg α⋅ (a - b)/2 = c . synti α

Tunnetut diagonaalit kaikki puolet tai kaksi puolta ja kulma

d -d₁ = √ (c²+ a b)

d -d₁ = √ (a²+ c² - 2 a c cos α)

d -d₁ = √ (b² + c²- 2 b c cos β)

Iskosceles -kolmion kehä 

P = a + b + 2c

Iskosceles trapezoidialue

Alueen laskemiseen on useita kaavoja tiedossa olevista tiedoista riippuen. Seuraava on tunnetuin pohjasta ja korkeudesta riippuen:

A = h⋅ (a + b)/2

Ja näitä muita voidaan käyttää myös:

-Jos sivut tunnetaan

A = [(a +b)/4] √ [4c² - (A - b)²-

-Kun sinulla on kaksi puolta ja kulma

A = (B + C COS α) C SEN α ​​= (A - C COS α) C SEN α

-Jos rekisteröidyn kehän säde tunnetaan ja kulma

A = 4 r² / Sin α = 4 r² / Sin β

-Kun emäkset ja kulma tunnetaan

A = a⋅b / sin α = a⋅b / sen β 

-Jos trapetsia voidaan rekisteröidä ympärysmitta

A = c⋅√ (a⋅b) = m⋅ity (a⋅b) = r⋅ (a + b)/2

-Tunnetaan toistensa kanssa muodostuvat diagonaalit ja kulma

A = (D₁²/2) Sen γ = (D₁² / 2) Sen δ 

-Kun sinulla on sivu, mediaani ja kulma

A = MC.SIN α = MC.SEN β

Kiristetty ympärysradio

Ainoa ISCELES -trapetsoideilla on rajattu kehä. Jos pääpohja tunnetaan, sivu C ja diagonaali D₁, Sitten trapetsin neljän kärjen läpi kulkevan kehän säde R on:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -D₁)

Missä p = (a + c + d₁) / 2

Esimerkkejä šosceles trapezoidista

ISCELES Trapezoidi ilmestyy suunnittelukentällä, kuten kuvassa 2 nähdään. Ja tässä meillä on joitain lisäesimerkkejä:

Arkkitehtuurissa ja rakentamisessa

Muinaiset inkat tiesivät Basosceles trapezoidia ja käyttivät sitä rakennuselementtinä tässä Cuzcon ikkunassa, Peru:

Kuva 5 . Ikkuna, jossa on Coricanchan trapetsoidinen muoto, Cuzco. Lähde: Wikimedia Commons.

Ja tässä trapetsoidi ilmestyy jälleen puhelussa Trapetsoidinen arkki, Usein käytetty materiaali rakenteessa:

Kuva 6. Trapetsoidinen metallilevy suojaa väliaikaisesti rakennuksen ikkunoita. Lähde: Wikimedia Commons.

Suunnittelussa

Huomasimme jo, että šosceles trapezoidi esiintyy arjen esineissä, osallistavia ruokia, kuten tämä suklaapalkki:

Kuva 7. Suklaapalkki, jonka kasvot ovat muotoiltuja samanaikaisesti. Lähde: PxFuel.

Ratkaisut

- Harjoitus 1

ISCELES Trapetsoidi perustuu kuin 9 cm, pohja alle 3 cm ja sen diagonaalit 8 cm. Laskea:

Se voi palvella sinua: Yleinen Parabola -yhtälö (esimerkit ja harjoitukset)

a) sivu

b) korkeus

c) kehä

d) Ärea

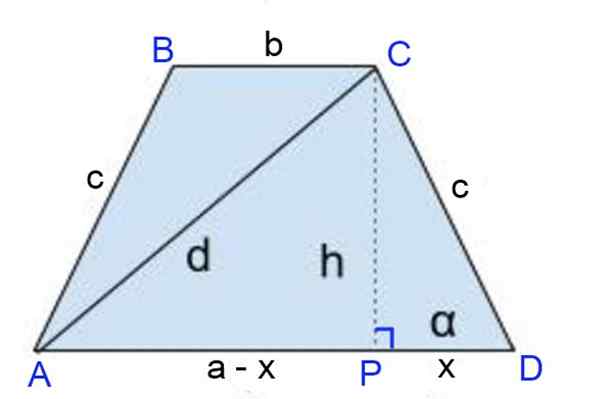Kuva 8. Järjestelmä harjoitukselle 1. Lähde: f. Zapata

Liittää jhk

Korkeus CP = H vedetään, missä korkeuden jalka määrittelee segmentit:

Pd = x = (a-b)/2 ja 

AP = a - x = a - a/2 + b/2 = (a + b)/2.

Pythagoras -lauseen läpi DPC: n suorakulmiokolmioon:

c² = h² + (A - b)² /4

Ja myös APC: n suorakulmion kolmio:

d -d² = h² + AP² = h² + (A+B)² /4

Lopuksi jäsen on vähennetty, ensimmäinen yhtälö ensimmäisen ja yksinkertaistaa:

d -d² - c² = ¼ [(a+b)² - (A-B)²] = ¼ [(A+B+A-B) (A+B-A+B)]

d -d² - c² = ¼ [2a 2b] = a b

c²= D² - A b ⇒ c = √ (d² - a b) = √ (8² - 9⋅3) = √37 = 6,08 cm

Ratkaisu b

h² = D² - (A+B)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Liuos C

Kehä = a + b + 2 c = 9 + 3 + 2⋅6 083 = 24 166 cm

Liuos D

Pinta -ala = h (a+b)/2 = 5,29 (12)/2 = 31,74 cm

- Harjoitus 2

Siellä on šosceles trapezoid. Päättää:

a) sivun sivu

b) kehä

c) alue

d) kulmat

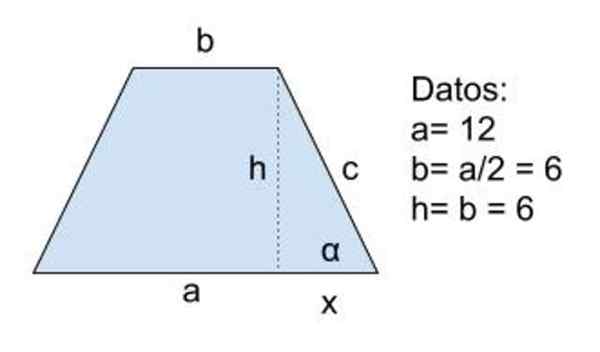Kuva 8. Harjoitus 2. Lähde: f. Zapata

Liittää jhk

Tiedot: a = 12, b = a/2 = 6 ja h = b = 6

Jatkamme tällä tavalla: korkeus H on piirretty ja Pythagoras -lause sovelletaan hypotenusikolmioon "C" ja Catetos H ja X:

c² = h²+XC²

Sitten sinun on laskettava korkeusarvo tiedoista (h = b) ja cateto x: 

a = b + 2 x ⇒ x = (a-b)/2

Aiempien lausekkeiden korvaaminen:

c² = b²+(A-B)²/2²

Nyt numeeriset arvot esitetään ja yksinkertaistetaan:

c² = 62+ (12-6) 2/4

c² = 62 (1+¼) = 62 (5/4)

Saada:

C = 3√5 = 6,71 cm

Ratkaisu b

Kehä p = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Liuos C

Pohjojen korkeuteen ja pituuteen perustuva alue on:

A = h⋅ (a + b)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Liuos D

Kulma α, joka muodostaa sivun pääpohjan kanssa, saadaan trigonometrialla:

Tan (α) = h / x = 6/3 = 2

α = arktan (2) = 63,44º

Toinen kulma, joka muodostaa sivun pienen emäksen kanssa, on β, joka on a α: n täydentävä:

β = 180º - α = 180º - 63,44º = 116,56º

Viitteet

1. JA. -Lla. 2003. Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Campos, f. 2014. Matematiikka 2. Patria -toimitusryhmä.
3. Vapautettu, k. 2007. Tutustu monikulmioihin. Vertailuindeksiyhtiö.
4. Hendrik, V. 2013. Yleiset monikulmiot. Birkhäuser.
5. Iger. Matematiikka ensimmäisen lukukauden Tacaná. Iger.
6. Jr. Geometria. 2014. Monikulmio. Lulu Press, Inc.
7. Miller, Heeren ja Hornsby. 2006. Matematiikka: päättely ja sovellukset. Kymmenesosa.  Painos. Pearson -koulutus.
8. Patiño, m. 2006. Matematiikka 5. Toimitusohjelma.
9. Wikipedia. Trapetsi. Palautettu: on.Wikipedia.com