Tidecágono

Kuvio 1.- Vasemmalla tavallinen tridecácágone ja oikealla puolella Tšekin tasavallan 20 kruunun valuutta, jossa Bridcagon -muotoinen muoto on kirjoitettu kehässä, toisaalta siinä on Bohemian leijona ja toisella San Wenceslaolle, Patron, Patron Tšekin tasavallasta, joka on asennettu hevosen selässä. Lähde: f. Zapata.

Mikä on tridecágono?

TrideCagon on monikulmioperheen tasainen geometrinen hahmo ja joille on ominaista 13 sivua ja 13 kärkeä. Toinen nimi tälle monikulmiolle on Triskiadecágono, Numero on johdettu kreikkalaisesta.

13 puolta ovat linjasegmenttejä, jotka lopulta lähellä kuvion muotoilua. Polygonit, jotka on nimetty osapuolten määrän mukaan, ovat rikas inspiraation lähde arkkitehtuurille, rakentamiselle ja lukuisten esineiden, sekä taide- että utilitaristien, suunnittelulle.

Tridecágonon ominaisuudet

Tridecágono jakaa muiden polygonien kanssa seuraavat ominaisuudet ja ominaisuudet:

-Puolet, Ne ovat linjasegmenttejä, jotka on liitetty muodostamaan hahmo, jotka Tridecágonon tapauksessa ovat 13. Ne tunnistetaan pienillä kirjaimilla.

-Kärjet, Tätä kutsutaan peräkkäisten osapuolten risteyspisteisiin ja merkitään yleensä isoilla kirjaimilla. Tridecágonolla on 13 kärkeä.

-Kehä, vastaa sivujen summaa. Jos kaikilla puolilla on yhtä suuri mitta “A”, kehä on yksinkertaisesti 13 × A, mutta jos sivut ovat epätasa -arvoisia, kehä lisää jokaisen sivun pituuden.

-Keskusta, Piste pitää saman etäisyyden sekä kärjen että sivujen kanssa.

-Diagonaali, Linja, joka liittyy kärkipisteeseen toiseen ei -konseeriin kärjessä (peräkkäiset kärkipisteet yhdistyvät sivuilla).

-Sisäkulmat, Ne muodostuvat kuvion kahden vierekkäisen sivun ja monikulmion sisäosan väliin, ja sen kärki on yleinen kärki molemmille puolille.

Voi palvella sinua: Miletus sellainen lause

-Ulkokulmat, Ne ovat monikulmion ulkopuolella, yhden puolen ja yhden peräkkäisen sivun pidentymisen välillä ensimmäiseen.

-Radio, Tridecágonin etäisyys etäisyys.

-Keskikulma, Se on se, jonka kärki on monikulmion keskipiste.

-Apoteemi, Segmentti, joka liittyy toisen puolen keskustaan ​​kuvion keskikohtaan ja muodostaa 90º: ta tuon puolen kanssa.

Säännöllinen ja epäsäännöllinen ukkonen

Kolmet voivat olla:

-Säännöllinen, Kun kaikkien sen kolmentoista sivun mitta on sama ja sen sisäkulmat mittaavat samat.

-Epäsäännöllinen, Jos yhdellä tai useammalla sivulla on erilaiset toimenpiteet.

Tavallisen Tridecácágonen tapauksessa seuraavia kaavoja voidaan soveltaa:

Sisäkulma

Tavallisen monikulmion kohdalla kaava, joka sallii laskemisen sisäkulman arvon, on:

Missä n edustaa sivujen lukumäärää, mikä tässä tapauksessa on 13. Tämän arvon kanssa se on:

I = (11 × 180º)/13 ≈ 152.Kolmas

Diagonaalit

Diagonaalien lukumäärä lasketaan seuraavalla kaavalla, jopa voimassa, jos monikulmio on epäsäännöllinen:

N = 13 tulokselle:

D = 13 × 10/2 = 65 diagonaalia

Apoteemi

Apoteemin L arvo_-Lla  Se lasketaan seuraavalla kaavalla, koska se on "A" sivun pituus:

Lens_-Lla ≅ 2.0286a

Alue

Jos kehä P ja apoteemin pituus l_-Lla, Tridecágonon alue on laskettu:

A = (P × L_-Lla)/2

A -puolesta riippuen kaava pysyy:

A = (13a × l_-Lla)/2

Mittauksen korvaaminen_-Lla Edellisestä osasta saadaan kaava alueelle, joka riippuu vain sivun pituudesta:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Voi palvella sinua: hypergeometrinen jakauma: kaavat, yhtälöt, malli

Harjoittele

Jos 20 mm: n kruunun halkaisija on 26 mm, kuinka paljon valuutan ympyrään rekisteröidyn Tridecágonon sivu- ja pinta -ala?

Ratkaisu

Kuviosta on suorakulmiokolmio, jonka luokat ovat apoteemi ja puolet sivun pituudesta, hypotenusa on yhtä suuri kuin valuutan säde, joka on puolet halkaisijasta. Koska tämän arvo on 26 mm, radio r on yhtä suuri kuin 13 mm.

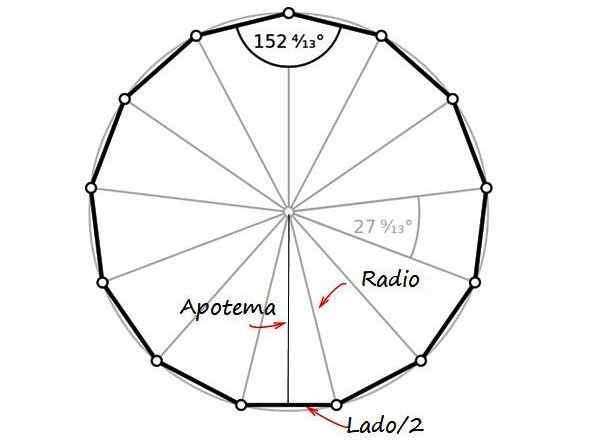Kuva 2. Radio, apoteemi ja puolet trindecagonin sivusta muodostavat suorakulmion kolmion. Lähde: Wikimedia Commons/F. Zapata.

Kirjoittanut Pythagoras -lause:

Koska l_-Lla ≈ 2.0286a, sinulla on:

R -² = (2.0286a)² + (0.5.)² = 4.3652a²

Sivu on:

Tällä arvolla valuutan alue on:

≈ 13.186a² = 13.186 (6.222 mm)² = 510.5 mm²

Lukija jätetään vertaamaan tätä tulosta alueen kanssa, joka saadaan olettamalla, että valuutta on säteen pyöreä r = 13 mm.

Kuinka tridecágono on?

Tavallinen trindejagon on monikulmio, joka ei myönnä tarkkaa rakennetta käyttämällä vain sääntöä ja kompassia, ts. Se ei ole rakennettava monikulmio. Ne ovat vain rakennettavia, ainakin teoriassa ne monikulmiot, joiden sivujen lukumäärä sisältää vain muodon tärkeimmät tekijät:

Alkeisumeroita sitä kutsutaan Fermat -serkut, Mutta numero 13, vaikka se on serkku, ei ole tätä muotoa.

Voit kuitenkin piirtää normaalin trindecagonin, joka on rekisteröity kehässä, jokaisella kärkipisteellä on risteys sen kanssa, ilman että sitä huomataan paljaalla silmissä. Tätä varten se on välttämätöntä.

Voi palvella sinua: obtuslangle -kolmio

Yksi tapa rakentaa säännöllinen Tridecácágone, vaikkakaan ei ainoa, on piirtäminen seuraavan animaation osoittamalla tavalla:

Kuva 3. Tavallisen Tridecagonin rakentaminen. Lähde: Wikimedia Commons.

Ja tämä toinen animaatio kuvaa myös kuinka tehdä Tridecágono suunnilleen säännön ja kompassin kanssa:

Kuva 4.- Vaihtoehtoinen tapa rakentaa suunnilleen tavallinen TrideCagon sääntöllä ja kompassilla. Lähde: Wikimedia Commons.

Esimerkkejä Tridecágelista

Kovera ja kupera ukkonen

Kun Tridecágonon sisäkulmat ovat alle 180º, kuva on kupera, kun taas yksi tai useampi sisäkulma on suurempi kuin 180º, niin Tridecágono on kovera.

Tavallinen Tridecácágon on kupera, koska sen sisäkulmat mittaavat noin 152.Kolmas kukin.

Tridecágonon käyttö numismatiikassa

Tšekin kruunu

Numeromatiikka on kolikoiden, mitalien, lippujen ja sirujen tiede. Monien puolien monikulmiot ovat ihanteellisia koristeellisina elementteinä kolikoiden suunnittelussa, etenkin ne, joilla on monia puolia, kuten Tridecágono.

Kaikki kolikot eivät ole pyöreitä, mutta monien sivujen monikulmiot muistuttavat pyöreää muotoa, mitä enemmän sivuja sillä on, sitä suurempi lähestymistapa. Siksi kolikoiden suunnittelijat käyttävät monikulmioita monilla puolilla tuodakseen mallin omaperäisyyden ripauksen.

Tällä tarkoituksella käytetään erilaisia ​​monikulmioita, kuten ylempi valuutta, nimeltään kruunu ja Tšekin tasavallasta, hyvä esimerkki Tridecágonon käytöstä suunnitteluelementtinä.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Piirustus. Tavallinen monikulmikone. Palautettu: Piirustus.com.
3. Hartley, m. Tridecagonin rakentaminen. Palautettu: YouTube.com
4. Wikipedia. Rakennettava monikulmio. Palautettu: on.Wikipedia.org.
5. Wikiwand. Sidos. Toipunut: Wikiwand.com.