Acutangle -kolmio

Mitkä ovat acutangulus -kolmiot?

Se Acutangulus -kolmiot Ne ovat niitä, joiden kolme sisäkulmaa ovat akuutteja kulmia; Eli kunkin kulman mitta on alle 90 ° astetta. Koska meillä ei ole mitään suorakulmaa, meillä on, että Pythagoras -lause ei täyty tälle geometriselle hahmolle.

Siksi, jos haluamme jonkin tyyppistä tietoa jostakin sen sivuista tai kulmista, on välttämätöntä käyttää muita lauseita, joiden avulla voimme käyttää näitä tietoja. Ne, joita voimme käyttää, ovat rintalause ja kosinin lause.

Acutlangle -kolmion ominaisuudet

Niiden ominaisuuksien joukossa, jotka tällä geometrisella hahmolla on, voimme korostaa niitä, jotka annetaan kolmion yksinkertaisella tosiasialla. Näiden joukossa meidän on:

- Kolmio on monikulmio, jolla on kolme sivua ja kolme kulmaa.

- Sen kolmen sisäisen kulman summa on yhtä suuri kuin 180 °.

- Kahden sivun summa on aina suurempi kuin kolmas.

Katsotaan esimerkiksi seuraava ABC -kolmio. Yleensä tunnistamme heidän sivut pienellä kirjaimella ja niiden kulmilla pääoman kirjaimella, niin että sivulla ja heidän vastakkaisella kulmalla on sama kirjain.

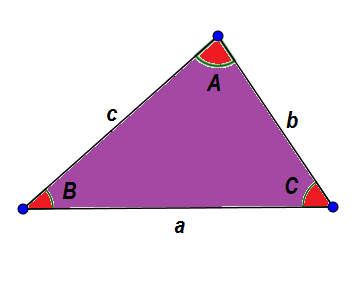
Jo annettujen ominaisuuksien takia tiedämme sen:

A + B + C = 180 °

A + B> C, A + C> B ja B + C> A

Tämän tyyppisen kolmion muusta erottava pääpiirte on se, että kuten jo mainitsimme, sen sisäkulmat ovat akuutteja; Eli kunkin kulman mitta on alle 90 °.

Acutangulus -kolmiot yhdessä sotkuisten kolmioiden kanssa (ne, joissa yhdellä sen kulmista on yli 90 °), ovat osa vinoja kolmioita asetettuja. Tämän sarjan muodostavat kolmiot, jotka eivät ole suorakulmioita.

Voi palvella sinua: mitkä ovat vertauksen elementit? (Osat)

Ollessaan osa vinoja kolmioita, meidän on ratkaistava ongelmat, joissa Acutangulus -kolmiot puuttuvat asiaan, on käytettävä rintalausetta ja kosinuslausetta.

Rintojen lause

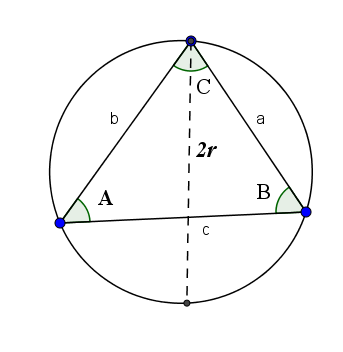
Rintalause vakuuttaa, että toisella puolella oleva syy sen vastakkaisen kulman rintaan on yhtä suuri kuin kaksinkertainen ympyrän säde, jonka mainitun kolmion kolmella kärkipisteellä on. Tarkoittaen:

2r = a/sin (a) = b/sen (b) = c/sen (c)

Coseno -lause

Toisaalta Cosenon lause antaa meille nämä kolme yhtäläisyyttä kaikille ABC -kolmiolle:

-lla²= b² + c² -2BC*cos (a)

b -²= a² + c² -2AC*cos (b)

c²= a² + b -² -2AB*cos (c)

Nämä lauseet tunnetaan myös nimellä kosinin sinus- ja laki.

Toinen ominaisuus, jonka voimme antaa acutangous -kolmioista, on se, että kaksi näistä ovat samat, jos ne täyttävät seuraavat kriteerit:

• Jos heillä on kaikki kolme puolta.
• Jos heillä on sivu- ja kaksi kulmaa, jotka ovat yhtä suuret kuin toisiinsa.
• Jos heillä on kaksi puolta ja sama kulma.

Tyypit acutángulos -kolmiot

Acutangulus -kolmiot voidaan luokitella heidän puolensa mukaan. Nämä saattavat olla:

Kolmiot Tasasivuinen acutangulos

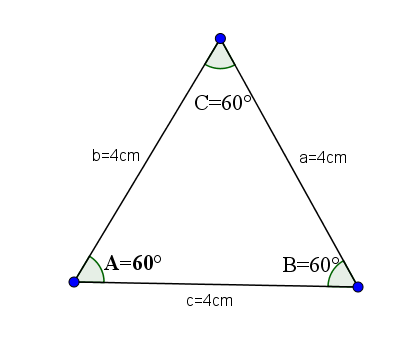
Ne ovat acutangulotiivisia kolmioita, joilla on kaikki yhtäläiset puolet, ja siksi kaikilla heidän sisäkulmillaan on sama arvo, mikä on A = B = C = 60 ° astetta.

Esimerkiksi, otetaan seuraava kolmio, jonka sivujen A, B ja C on arvo 4.

Iskosceles acutángulos -kolmiot

Näillä kolmioilla on akuutin sisäkulman lisäksi ominaisuus, että sillä on kaksi heidän yhtä suurta puolta ja kolmas, jota yleensä pidetään pohjana.

Esimerkki tämäntyyppisistä kolmioista voi olla yksi, jonka pohja on 3 ja sen kahden muiden puolen arvo on 5. Näillä toimenpiteillä se olisi kulmat vastustavat yhtä suuria puolia arvon 72,55 ° ja pohjan vastakkainen kulma olisi 34,9 °.

Voi palvella sinua: NULL Kulma: Määritelmä ja ominaisuudet, esimerkit, harjoitukset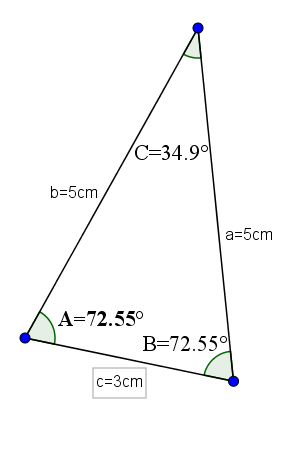

Scalene acutangulus -kolmiot

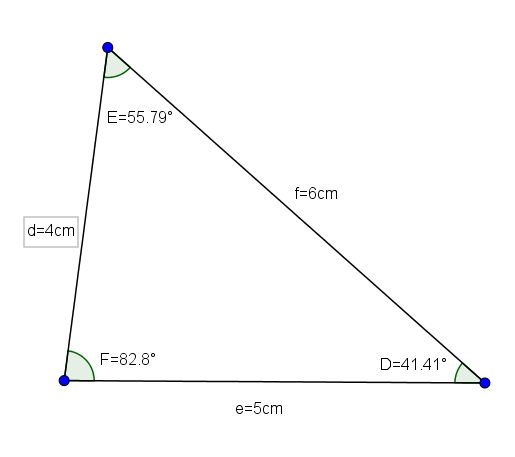
Nämä ovat kolmiot, joilla on kaikki eri puolet kahdesta kahteen. Siksi kaikki sen kulmat ovat alle 90 °: n lisäksi erilaisia ​​kahdesta kahteen.

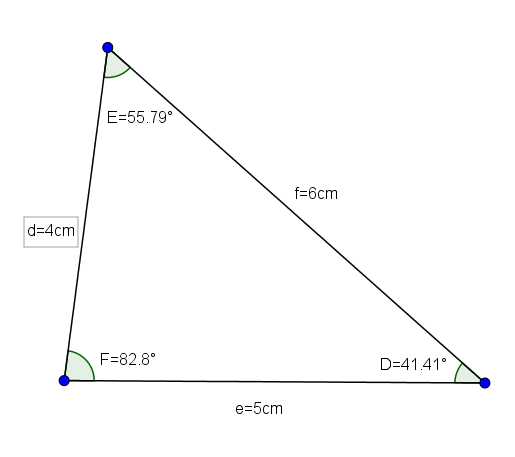
Triangle DEF (jonka mittaukset ovat d = 4, e = 5 ja f = 6 ja sen kulmat ovat d = 41,41 °, e = 55,79 ° ja f = 82,8 °) on hyvä esimerkki acutangle -kolmion skaleenista.

Acutangles -kolmioiden ratkaisu

Kuten aiemmin totesimme, ongelmien ratkaisemiseksi, joissa acutangulus -kolmiot puuttuvat asiaan.

Esimerkki 1

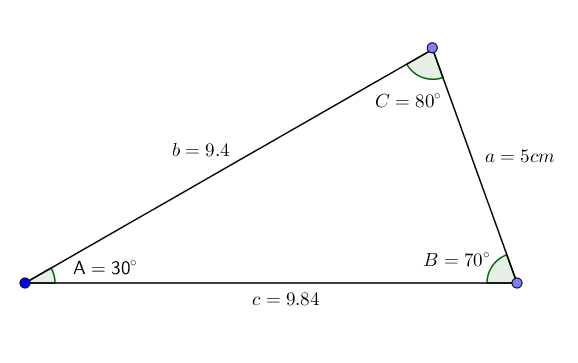
Annetaan ABC -kolmio, jonka kulmat A = 30 °, B = 70 ° ja sivu A = 5cm, haluamme tietää kulman C ja sivujen B ja C arvon.

Ensimmäinen asia, jota teemme.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Selvitämme c ja meillä on:

C = 180 ° - 100 ° = 80 °

Kuten tiedämme kolme kulmaa ja yhden puolen, voimme käyttää rintojen lausetta jäljellä olevien sivujen arvon määrittämiseen. Lauselle meidän on:

a/sin (a) = b/sen (b) ja a/sen (a) = c/(sin (c)

Poistamme yhtälön ja meidän on:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Nyt meidän on vain laskettava C: n arvo. Jatkamme analogista kuin edellisessä tapauksessa:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Siksi saamme kaikki kolmiotiedot. Kuten voimme huomata, tämä kolmio tulee skannaus kolmio -luokkaan.

Esimerkki 2

Annetaan puolustuskolmio, jolla on sivut d = 4cm, e = 5cm ja f = 6cm, haluamme tietää mainitun kolmion kulmien arvon.

Tätä tapausta käytämme kosinin lakia, joka kertoo meille:

Voi palvella sinua: Kahden peräkkäisen numeron neliöiden summa

d -d²= e² + F² - 2EFCOS (D)

Tästä yhtälöstä voimme tyhjentää cos (d), mikä johtaa:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

Sieltä meidän on laituri 41.41 °

Senom -lauseen avulla meillä on nyt seuraava yhtälö:

D/(sin (d) = e/(sin (e)

Sen (E) puhdistaminen, meidän on:

sin (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Sieltä meidän täytyy.79 °

Lopuksi, että kolmion sisäkulmien summa on 180 °, meidän on.8 °.