Tasakylkinen kolmio

Iskosceles -kolmiossa on kaksi yhtä suurta sivua ja yksi erilainen

Mikä on Iskosceles -kolmio?

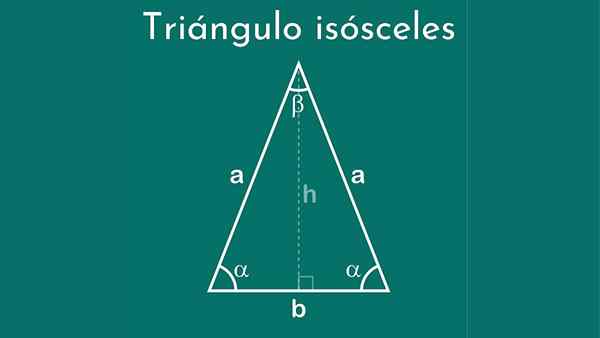
Eräs tasakylkinen kolmio Se on kolmipuolinen monikulmio, jossa kahdella niistä on sama mitta ja kolmas puoli erilainen mitta. Tätä viimeistä puolta kutsutaan pohjaksi. Tämän ominaispiirteen ansiosta tämä nimi annettiin, mikä kreikkalaisella tarkoittaa "yhtäläisiä jalkoja".

Kolmiot ovat monikulmioita, joita pidetään geometrian yksinkertaisimpana, koska ne muodostuvat kolme puolta, kolme kulmaa ja kolme kärkeä. He ovat niitä, joilla on vähiten sivuja ja kulmia muihin monikulmioihin, mutta niiden käyttö on erittäin laajaa.

ISCELES -kolmioiden ominaisuudet

Iskosceles -kolmio luokiteltiin käyttämällä sen sivujen mittaa parametrina, koska kaksi sen sivua on yhdenmukainen, ts. Niillä on sama pituus.

Sisäisten kulmien amplitudin mukaan samasosat -kolmiot luokitellaan seuraavasti:

• Sintakelit suorakulmion kolmio: Kaksi sen sivuista ovat samat. Yksi sen kulmista on suora (90^jompikumpi) Ja muut ovat samat (45^jompikumpi jokainen)
• Šosceles foluse -kolmio: Kaksi sen sivuista ovat samat. Yksi sen kulmista on tylsä ​​(> 90^jompikumpi-A.
• Šosceles acutlangle -kolmio: Kaksi sen sivuista ovat samat. Kaikki sen kulmat ovat akuutteja (< 90^jompikumpi), Missä kahdella on sama mitta.

Komponentit

• Mediaani: Se on linja, joka lähtee keskipisteestä toiselta puolelta ja saavuttaa vastakkaisen kärjen. Kolme väliainetta osallistuvat pisteeseen nimeltä Baricentro tai Centroid.
• Puolustaja: Se on puoliksi oikea, joka jakaa kunkin kärjen kulman kahteen yhtä suureen omaan kulmaan. Siksi sitä kutsutaan symmetria -akseliksi, ja tämän tyyppisillä kolmioilla on vain yksi.
• Mediatrix: Se on segmentti, joka on kohtisuorassa kolmion sivulle, joka on peräisin tämän keskeltä. Kolmiossa on kolme mediaatiaa ja osallistuvat pisteen nimeltä Ympyräkeskeinen.
• Korkeus: Se on linja, joka kulkee vastapäätä olevasta kärjestä ja myös tämä viiva on kohtisuorassa siihen puoleen. Kaikilla kolmioilla on kolme korkeutta, jotka osuvat samanaikaisesti Ortocenter -nimisessä pisteessä.

Iskosceles -kolmioominaisuudet

ISCELES -kolmiot määritetään tai tunnistetaan, koska niillä on useita niitä edustavia ominaisuuksia, jotka ovat peräisin suurten matemaatikkojen ehdottamista lauseista:

Sisäkulmat

Sisäisten kulmien summa on aina yhtä suuri kuin 180^jompikumpi.

Sivujen summa

Kahden osapuolen mittojen summan tulisi aina olla suurempi kuin kolmannen puolen mitta, a + b> c.

Yhtenäiset osapuolet

ISCELES -kolmioilla on kaksi puolta, joilla on sama mitta tai pituus; toisin sanoen he ovat yhdenmukaisia, ja kolmas puoli on erilainen kuin nämä.

Yhdenmukaiset kulmat

ISOSCELES -kolmiot tunnetaan myös nimellä isoangulous kolmio, koska niillä on kaksi kulmaa, joilla on sama mitta (yhtenäinen). Nämä sijaitsevat kolmion juuressa, vastakkain sivuilla, joilla on samanpituus.

Voi palvella sinua: trapetsoidinen prisma

Tämän vuoksi lause, joka vahvistaa sen:

"Jos kolmiolla on kaksi yhdenmukaista puolta, myös kyseisiin osapuoliin vastakkaiset kulmat ovat yhtenäisiä". Siksi, jos kolmio on samasosaa, sen tukikohdat ovat yhdenmukaisia.

Esimerkki:

Seuraavassa kuvassa havaitaan ABC -kolmio. Piirrät puoletorinsa kulman B kärjestä pohjaan, kolmio on jaettu kahteen BDA- ja BDC -kolmioon:

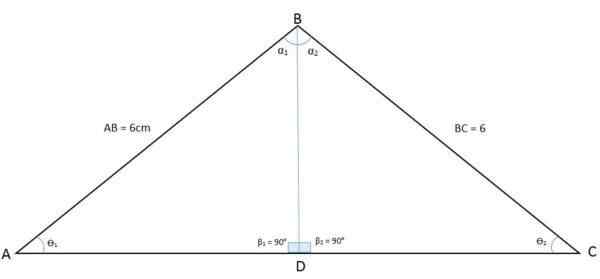Bisektori, joka jakaa kahteen kolmioon, joka on yhtä suuri kuin ISCELES -kolmio

Tällä tavoin kärjen B -kulma jaettiin myös kahteen yhtä suureen kulmaan. Puoli on nyt yleinen puoli (BD) näiden kahden uuden kolmion välillä, kun taas sivut AB ja BC ovat yhteneviä puolia. Näin on sivu, kulma, sivu (LAL).

Se osoittaa, että kärkipisteiden A ja C kulmilla on sama mitta, samoin kuin voidaan osoittaa, että koska BDA- ja BDC -kolmiot ovat yhdenmukaisia, myös AD- ja DC -puolet ovat.

Korkeus, mediaani, mediarix ja puolustaja ovat sattumaa

Iskososceles -kolmion pohjan vastapäätä vastapäätä olevasta kärjestä vedetty viiva on samanaikaisesti korkeus, mediaani ja mediariisi, samoin kuin puolustaja suhteessa pohjan vastakkaiseen kulmaan.

Kaikki nämä segmentit osuvat samaan aikaan, joka edustaa niitä.

Esimerkki:

Seuraavassa kuvassa ABC -kolmio havaitaan keskipitkällä M -pisteellä, joka jakaa emäksen kahteen BM- ja CM -segmenttiin.

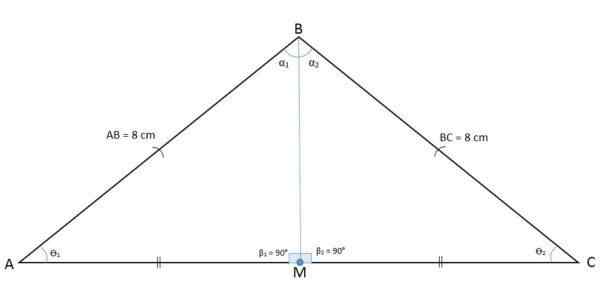Korkeus, mediaani, mediarix ja puolustaja ovat sattumaa

Kun piirtät segmentin pisteestä M vastakkaiseen kärkeen, saadaan määritelmän mukaan mediaani AM, joka on suhteessa kärkeen A ja BC -puolelle.

Koska AM -segmentti jakaa ABC -kolmion kahteen yhtä suureen kolmioon AMB: hen ja AMC: hen, se tarkoittaa, että sivu-, kulma-, sivu-, sivu- ja siksi AM -tapaus on myös Bâc: n puolustaja.

Siksi puoliaja on aina yhtä suuri kuin mediaani ja päinvastoin.

AM -segmentti muodostaa kulmat, joilla on sama mitta AMB- ja AMC -kolmioille; toisin sanoen ne ovat täydentäviä, joten kunkin mitta on:

Lääketieteellinen. (Amb) + Med. (AMC) = 180^jompikumpi

2 _* Lääketieteellinen. (AMC) = 180^jompikumpi

Lääketieteellinen. (AMC) = 180^jompikumpi ÷ 2

Lääketieteellinen. (AMC) = 90^jompikumpi

Voidaan tietää, että kolmion pohjaa koskevan AM -segmentin muodostamat kulmat ovat suorat, mikä osoittaa, että tämä segmentti on täysin kohtisuorassa pohjaan nähden.

Siksi se edustaa korkeutta ja mediatrixiä tietäen, että m on keskipiste.

Siksi linja AM:

• Edustaa BC: n korkeutta.
• On keskikokoinen.
• Se sisältyy BC Mediatrixiin.
• Se on kärkipisaran â

Suhteelliset korkeudet

Korkeuksilla, jotka ovat suhteessa yhtä suuriin puoliin, on myös sama mitta.

Voi palvella sinua: Täydelliset numerot: Kuinka tunnistaa ne ja esimerkkejä

Koska sammal -kolmiossa on kaksi yhtä suurta sivua, sen kaksi vastaavaa korkeutta ovat myös samat.

Orocentro-, Baricentro-, Incentro- ja Colecentro -kolinsidit

Kun pohjaan liittyvät korkeudet, mediaanit, puolustaja ja mediatriisi ovat samanaikaisesti saman segmentin, ortokeskuksen, Baricentro, Incentre ja Ympyräkeskeisyys ovat kolineaalisia pisteitä, ts. Ne löytyvät samalta linjalta:

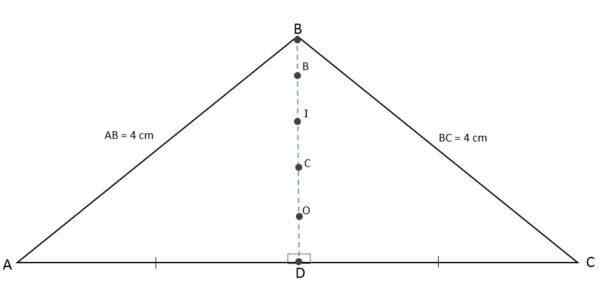Ortocenter, Baricentro, Incentro ja Ympyrä

Iskosceles -kolmioiden laskenta

Kuinka kehä lasketaan?

Polygonin kehä lasketaan sivujen summan perusteella.

Kuten tässä tapauksessa tasavirtakolmiolla on kaksi puolta samalla tavalla, sen kehä lasketaan seuraavalla kaavalla:

P = 2_*(Side a) + (sivu B).

Kuinka laskea korkeus?

Korkeus on pohjaan kohtisuorassa oleva viiva, jakaa kolmio kahteen osaan, jotka ovat yhtä suuret kuin ulottumalla vastakkaiseen kärkipisteeseen.

Korkeus edustaa vastakkaista Catoto (A), puolet pohjasta (b/2) viereiseen Catotoon ja “A” -puolelle edustaa hypotenusia.

ISCELES -kolmion korkeuden laskeminen

Käyttämällä Pythagoras -lausetta, korkeuden arvo voidaan määrittää:

-lla² + b -² = c²

Missä:

-lla² = korkeus (h).

b -² = B / 2.

c² = puoli a.

Näiden arvojen korvaaminen Pythagoras -lauseessa ja puhdistamalla korkeus:

h² + (b - / 2)² = -lla²

h² + b -² / 4 = -lla²

h² = -lla² - b -² / 4

H = √ (-lla² - b -² / 4).

Jos yhtenäisten sivujen muodostama kulma tunnetaan, korkeus voidaan laskea seuraavalla kaavalla:

Kuinka laskea alue?

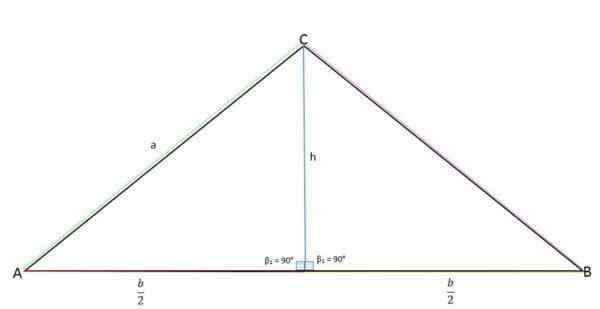
Kolmiot lasketaan aina samalla kaavalla, kertomalla pohja korkeudella ja jakamalla 2:

On tapauksia, joissa vain kolmion kahden puolen mitat tunnetaan ja niiden välillä muodostettu kulma. Tässä tapauksessa alueen määrittämiseksi on tarpeen soveltaa trigonometrisiä syitä:

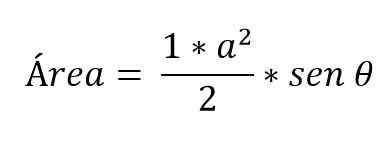
Kuinka laskea kolmion pohja?

Koska tasavirtakolmiolla on kaksi yhtä suurta puolta, sen pohjan arvon määrittämiseksi on tarpeen tietää ainakin korkeuden mitta tai yksi sen kulmasta.

Pythagoras -lausetta käytetään korkeuden, käytetään:

-lla² + b -² = c²

Missä:

-lla² = korkeus (h).

c² = puoli a.

b -² = B / 2, ei tunneta.

Selvitämme b² kaavasta ja meidän on:

b -² = a² - c²

B = √ a² - c²

Koska tämä arvo vastaa puolta emäksestä, se on kerrottava 2: lla, jotta voidaan saada ISCELES -kolmiopohjan täydellinen mitta:

B = 2 _* (√ a² - c²-A

Jos trigonometriaa tiedetään, että vain sen yhtäläisten sivujen ja niiden välinen kulma on vain, mikä vetää viivan kärjen kärjestä pohjaan, joka jakaa Kassceles -kolmion kahteen suorakulmioon kolmioon.

Tällä tavalla puolet pohjasta on laskettu:

Myös pohjaa vastustavan kärjen korkeuden ja kulman arvo on myös tiedossa. Tällöin trigonometrialla emäs voidaan määrittää:

Harjoitukset

Ensimmäinen harjoitus

Löydä ABC -kolmion alue, tietäen, että kaksi sen sivua on 10 cm ja kolmas puoli mittaa 12 cm.

Se voi palvella sinua: Antidervative: Kaavat ja yhtälöt, esimerkit, harjoitukset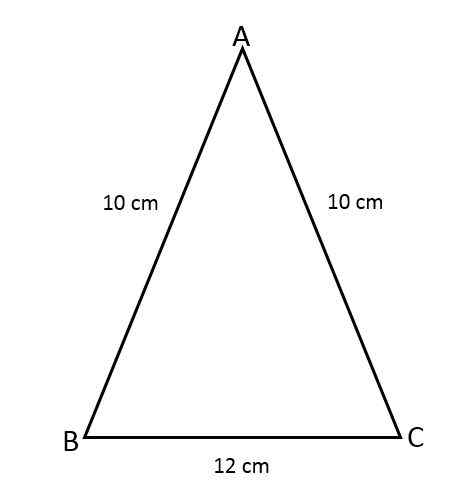

Ratkaisu

Kolmion alueen löytämiseksi se on välttämätöntä.

Seuraavat tarkkojen kolmiotiedot ovat saatavilla:

• Yhtä suuret sivut (a) = 10 cm.
• Pohja (b) = 12 cm.

Arvot korvataan kaavassa:

Toinen harjoitus

Kaksitasoisen kolminkertaisen kahden yhtä suuren sivun pituus on 42 cm, näiden sivujen liitto muodostaa kulman 130^jompikumpi. Määritä kolmannen puolen arvo, kyseisen kolmion ja kehän pinta -ala.

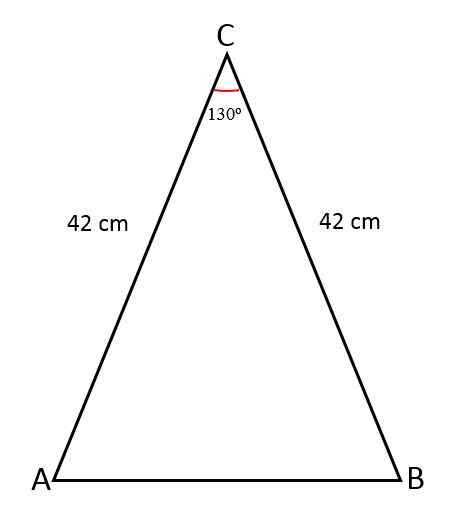
Ratkaisu

Tässä tapauksessa näiden välillä tunnetaan sivujen ja kulman mittaukset.

Puuttuvan sivun, toisin sanoen kyseisen kolmion pohjan, tietäminen, siihen piirretään viiva, joka on piirretty, jakamalla kulma kahteen yhtä suureen osaan, yksi jokaiselle muodostetulle suorakaiteen kolmiolle.

• Yhtä suuret sivut (a) = 42 cm.
• Kulma (ɵ) = 130^jompikumpi

Nyt trigonometrialla lasketaan puolen arvon arvo, joka vastaa puolta hypotenusista:

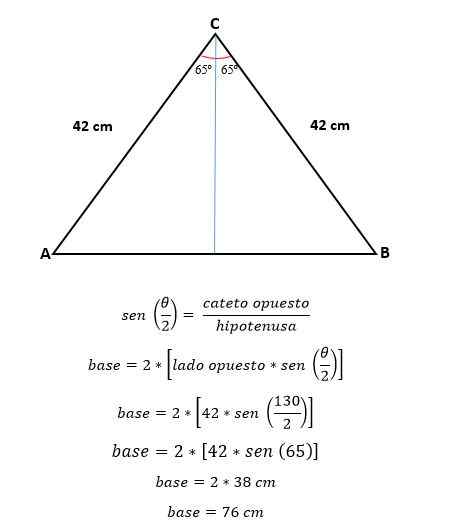
Alueen laskemiseksi on tarpeen tietää kyseisen kolmion korkeus, joka voidaan laskea trigonometrialla tai Pythagoras -lauseella, nyt kun pohjan arvo oli jo määritetty.

Trigonometrialla on:

Kehä on laskettu:

P = 2_*(Side a) + (sivu B).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Kolmas harjoitus

Laske tasaiskansomin kolmion sisäkulmat tietäen, että peruskulma on â = 55^jompikumpi

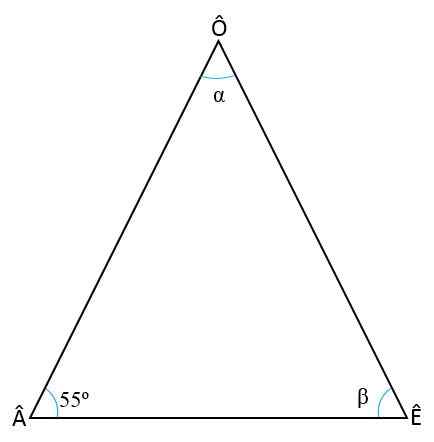
Ratkaisu

Kaksi puuttuvaa kulmaa (ê ja ô) on tarpeen muistaa kolmioiden kaksi ominaisuutta:

• Jokaisen kolmion sisäkulmien summa on aina = 180^jompikumpi-

 + ê + ô = 180 ^jompikumpi

• ISCELES -kolmiossa pohjan kulmat ovat aina yhdenmukaisia, toisin sanoen niillä on sama mitta, siksi:

 = ô

Ê = 55^jompikumpi

Kulman ê: n arvon määrittämiseksi ensimmäisen säännön muiden kulmien arvot korvataan ja ê puhdistetaan:

55^jompikumpi + 55^jompikumpi + Ô = 180 ^jompikumpi

110 ^jompikumpi + Ô = 180 ^jompikumpi

Ô = 180 ^jompikumpi - 110 ^jompikumpi

Ô = 70 ^jompikumpi.

Viitteet

1. Álvarez, E. (2003). Geometriaelementit: lukuisilla harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Álvaro Rendón,. R -. (2004). Tekninen piirustus: Aktiviteettikirja.
3. Enkeli, a. R -. (2007). Perusalgebra. Pearson -koulutus.
4. Arthur Goodman, L. H. ( 1996). Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
5. Baldor, a. (1941). Algebra. Havana: Kulttuuri.
6. José Jiménez, L. J -. (2006). Matematiikka 2.
7. Tuma, j. (1998). Engineering Mathematics Handbook. Wolfram Mathworld.