Sotkuinen kolmio

Selitämme, mikä on tylppä kolmio, sen elementit, ominaisuudet, tyypit, esimerkit ja ratkaistu harjoitus

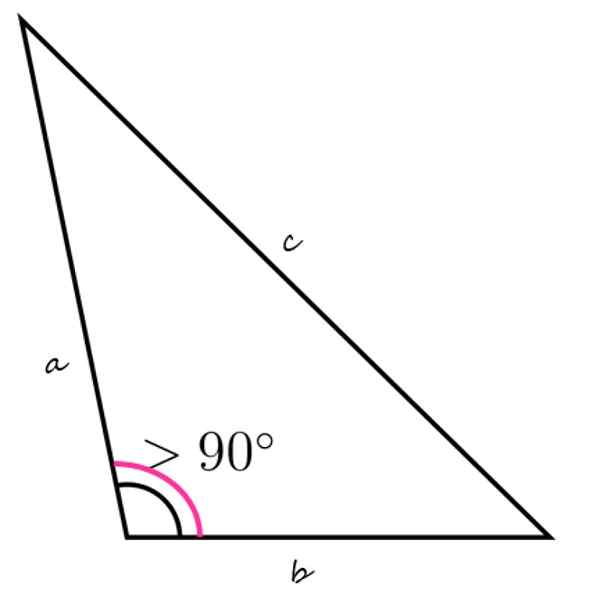Tyhjennä kolmiolle on tunnusomaista, että sisäkulma on yli 90º

Mikä on räikeä kolmio?

Eräs sotkuinen kolmio Se on litteä kuva, suljettu ja kolmella sivulla, ja se sisältää myös räikeän sisäkulman, toisin sanoen yli 90º ja alle 180º.

Mikä tahansa kolmio sisältää 3 sisäkulmaa, ja jos jokin niistä on tylsää, kaksi muuta ovat voiman avulla akuutissa, koska minkä tahansa kolmion sisäkulmien summa on aina yhtä suuri kuin 180º.

Yläkuvio näyttää esimerkin täpäristä kolmiosta, vasen alaosa sisäkulma on yli 90º. Jäljellä olevien sisäkulmien on lisättävä alle 90º, vain tällä tavalla on totta, että kolmen summa on yhtä suuri kuin 180º.

Tyhjentyvien kolmioiden lisäksi on olemassa akuuttomia kolmioita, jos kaikki sen sisäkulmat ovat akuutteja ja suorakulmiokolmiot, kun yksi sisäkulmista mittaa tarkalleen 90º.

Obuse -kolmioiden elementit

Obtusángulos -kolmioissa on yhteiset elementit kaikille kolmioille: ne ovat 3 -puolia litteää hahmoa, 3 sisäkulmaa ja 3 kärkeä. Lisäksi niillä on merkittäviä segmenttejä, joita kutsutaan Kettialaiset, kuten korkeus, mediaani ja mediatrix, ja pisteet, joissa cevialaiset leikkaavat.

Jokainen näistä elementeistä määritellään lyhyesti seuraavasti:

-Puolet, ovat segmentit, jotka muodostavat luvun.

-Kärjet, kunkin vierekkäisen puolen risteyspisteet.

-Sisäkulmat, Ne ovat kahden vierekkäisen sivun välissä, kuvion sisäpuolella, samoin kuin kulman kärki kolmiossa.

-Ulkokulmat, Ne ovat toisen sivun ja viereisen puolen pidennyksen välissä, kuvan ulkopuolella, kärkipiste on yleinen, sekä kolmio että kulma. Sisäkulman ja sen ulkoisen viereisen kulman välisen toimenpiteen summa on 180º, niin että ne ovat täydentäviä kulmia.

Se voi palvella sinua: Tukey -testi: Mikä on esimerkiksi ratkaistu harjoitus

-Korkeus, Segmentin mitta on kohtisuoran segmentin mitta, joka liittyy vastakkaisella puolella tai tämän laajennuksella.

-Mediaani, linja, joka on suunnattu kärkipisteestä vastakkaisen puolen keskustaan.

-Mediarix, segmentti kohtisuorassa sivuun nähden ja se kulkee sen keskuksen läpi.

-Puolustaja, Se on segmentti, joka jakaa kolmion puoleen sisäkulmaan.

-Orocentro, Kolmen korkeuden risteyspiste.

-Barycenter, Kutsutaan myös Centroid, se on kohta, jossa kolme mediaania leikkaavat.

-Ympyrä, Täällä kolme lääkettä leikataan.

-Kannustaa, puoliarviointipiste.

Kun nämä käsitteet on tarkistettu, alla on kuvattu joitain viehätyskolmioiden merkittävimmistä ominaisuuksista.

Ominaisuudet

1.- Tyhjennä kolmion kolmen sisäkulman summa on 180º, siksi vain yksi sen sisäkulmista voi olla suurempi kuin 90º, kun taas jäljellä olevien kahden summa on alle 90º.

2.- Tyhjennän kolmion pisin puoli on vastakka.

3.- Tyhjennä kolminglassa akuutin kulman korkeuden korkeudet ylittävät vastakkaisten sivujen pidennykset.

4.- Tyhjennän kolmion ortokeskuksena on kuviosta.

5.- Tyhjennän kolmion ympäröivä.

6.- Neliö on mahdollista rekisteröidä vain täpärikolmioon, joka tukee yhtä neliön sivuista kolmion pisin puolella. Kaksi neliötä voidaan piirtää, mikä tukee kolmion lyhyimpiä puolia, jolloin kärkipiste ei ole rekisteröity (joka ei kosketa kolmion sivua).

Voi palvella sinua: Tidecágono

7.- Ole sivujen (a, b, c) putous kolmio, joka on pisin puoli. Seuraava eriarvoisuus on pätevä:

-lla²+b -² < c²

8.- Ne ovat kaksi tylsää kolmiota, joiden vastaavat sivut ovat (a, b, c) ja (u, v, w). Kunkin pisimmät sivut ovat C ja W, joten seuraava eriarvoisuus toteutuu:

A ∙ U + B ∙ V < c∙w

Tyypit estävät kolmiot

Tyhjät kolmiot voivat olla kahden tyyppisiä sivujensa pituuden mukaan:

• Sammutus
• Skaaleeni

Ne kuvataan lyhyesti alla:

Tasakylkinen kolmio

Se on yksi, jolla on kaksi yhtä suurta puolta ja erilainen, ts. Sen sivut ovat (A, A, C).

Kun tasavirta kolmio on molemmat tylsä, mitan “A” sivut ovat lyhyempiä ja “C” -puoli on pisin. Samojen sivujen väliin muodostuu täsmäinen kulma, kun taas kaksi akuuttia kulmaa ovat yhtä suuret ja muodostetaan sivujen "A" ja sivun "C" väliin.

Ja kuten edellisessä osassa todetaan, sivu "C", koska se on pisin, se vastustaa tylsää kulmaa.

Skaaleenikolmio

Skaleenikolmion kolmella puolella on erilainen mitta: (a, b, c).

Esimerkit

Esimerkki 1

Seuraavassa kuvassa näkyvä kolmio on obuse. Tyhjäkulma on γ = 114.5. ja varmistetaan, että kolmen sisäisen kulman summa on 180º:

114.5. + 36.8º + 28.6. ≈ 180º

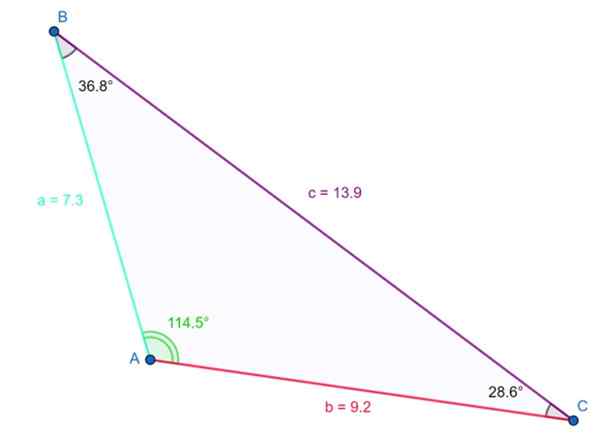Esimerkki tylsästä kolmiosta. Lähde: f. Zapata

Pisin sivumitta 13.9 yksikköä ja vastustaa tylsää kulmaa. Myös edellä mainittu eriarvoisuus täyttyy:

-lla²+b -² < c²

Voi palvella sinua: Suhteellisuussuhteet: Konsepti, esimerkit ja harjoitukset

Kyllä a = 7.3 ja B = 9.2, sitten:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Esimerkki 2

Calabi -kolmiossa on mahdollista sijoittaa suurin mahdollinen neliö kolmella eri tavalla kolmion sisällä, kuten seuraavassa kuvassa on esitetty.

Calabin kolmio on sameceles ja sotkuinen. Tyhjäkulma on noin 101.736 ° ja akuuttiset kulmat pohjamittaan molemmat 39.13., myös suunnilleen.

Liikuntaa

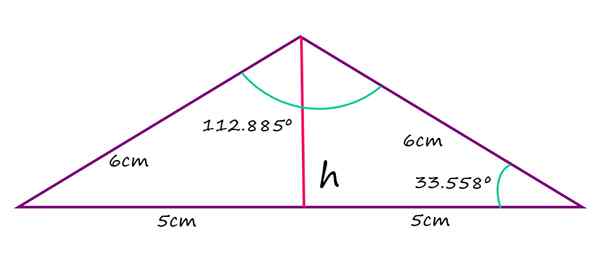
Tyhjennän tasapainon tasaiset puolet kolmiosta mittaa 6 cm, kun taas pisin sivu on 10 cm. Laske taistelukulman, jäljellä olevien agudoskulmien arvo ja korkeus mainitusta kärkistä pohjaan.

Ratkaisu

Kosinin lausetta voidaan käyttää löysäkulan kosinin löytämiseen. Sitten laskimen avulla määritetään kulma, merkitty γ: ksi.

Cosenon lause toteaa, että:

c² = a² +b -² - 2ab ∙ cos γ

Missä γ on kulma sivujen a ja b välillä. Koska kolmio on sammio, sivut A ja B ovat siksi: siksi:

c² = 2a² - toinen²∙ cos γ

COSTING COS -γ:

 Tyhjäkulma on -0 kosinikaari.38889, joka on noin 112.885º. Α: n arvo, 6 cm: n sivujen muodostama akuutti kulma 10 cm: llä on:

2α + 112.885º = 180º

α = (180 - 112.885)/2 = 33.558º

Šosceles foluse -kolmio. Lähde: f. Zapata

Mitä tulee kolmion korkeuteen, mitattuna pohjasta, se saadaan havaitsemalla, että tämä korkeus jakaa kolmion kahteen yhtä suureen suorakulmioon, hypotenusa on yhtä suuri kuin 6 cm ja emäs 5 cm. Tällöin Pythagoras -lause koskee sitä suoraan H: n arvon löytämiseksi: