Kolmioiden historia, elementit, luokittelu, ominaisuudet

Se kolmiot Ne ovat tasaisia ​​ja suljettuja geometrisia hahmoja, jotka koostuvat kolmesta puolesta. Kolmio määritetään kolmella viivalla, jotka leikataan kaksi tai kaksi, muodostuen toistensa kanssa kolmen kulman kanssa. Kolmion muotoinen muoto, joka on täynnä symbolismia, on läsnä lukemattomissa esineissä ja rakennuselementtinä.

Kolmion alkuperä on kadonnut historiassa. Arkeologisista todisteista tiedetään, että primitiivinen ihmiskunta tunsi hänet hyvin, koska arkeologiset jäännökset vahvistavat, että häntä käytettiin työkaluissa ja aseissa.

Kuvio 1. Kolmiot. Lähde: Julkiset alueet.

On myös selvää, että muinaisilla egyptiläisillä oli vankka tieto geometriasta ja erityisesti kolmionmuodosta. Heidät ruumiillistettiin monumentaalisten rakenteidensa arkkitehtonisiin elementteihin.

Rhind Papyrusissa on kaavoja kolmioiden ja trapetsialueiden laskemiseksi, samoin kuin joitain määriä ja muita alkeellisen trigonometrian käsitteitä.

Toisaalta tiedetään, että babylonialaiset pystyivät laskemaan kolmion ja muiden geometristen lukujen pinta -alan, jota he käyttivät käytännön tarkoituksiin, kuten maan jakautumiseen. He olivat myös tietoisia monista kolmioiden ominaisuuksista.

Muinaiset kreikkalaiset kuitenkin systemaattisesti monet nykypäivän geometriset käsitteet, vaikka suuri osa tästä tiedosta ei ollut yksinoikeutta, koska se oli varmasti jaettu näiden muiden muinaisten sivilisaatioiden kanssa.

[TOC]

Kolmion elementit

Minkä tahansa kolmion elementit on merkitty seuraavassa kuvassa. Niitä on kolme: kärjet, sivut ja kulmat.

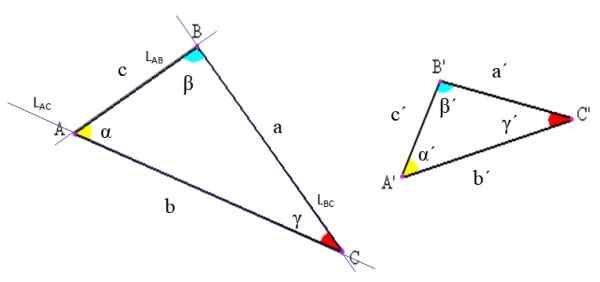Kuva 2. Kolmioiden ja niiden elementtien merkintä. Lähde: Wikimedia Commons, muokattu F. Zapata

-Kärjet: Nämä ovat linjojen leikkauspisteet, joiden segmentit määrittävät kolmion. Esimerkiksi ylemmässä kuvassa viiva L_Ac joka sisältää AC -segmentin, leikkaa viivan l_Ab joka sisältää segmentin ab vain kohdassa A.

-Puolet: Jokaisen parin kärjen välillä on piirretty linjasegmentti, joka muodostaa kolmion toisen puolen. Tätä segmenttiä voidaan merkitä päiden kirjaimilla tai tietyn kirjeen avulla kutsuaksesi sitä. Kuvion 2 esimerkissä AB -puolta kutsutaan myös "c".

-Kulmat: Kummankin puolen välillä, jolla on yhteinen kärkipiste, kulma on peräisin. Kulma on yleensä merkitty kreikkalaisella kirjaimella, kuten alussa todettiin.

Tietyn kolmion rakentamiseksi tietyllä muotolla ja koolla on vain joitain seuraavista tietojoukkoista:

-Kolme puolta, melko ilmeinen kolmion tapauksessa.

-Kaksi puolta ja niiden välinen kulma, ja jäljellä oleva puoli vedetään heti.

-Kaksi kulmaa (sisäistä) ja niiden välinen sivu. Laajennuksen mukaan kaksi puuttuvaa sivua piirretään ja kolmio on valmis.

Merkintä

Yleensä kolmioiden merkinnässä käytetään seuraavia yleissopimuksia: Perices on merkitty isoilla kirjaimilla, sivuilla, joissa on pienet latinalaiset kirjaimet ja kulmat kreikkalaisilla kirjaimilla (katso kuva 2).

Tällä tavoin kolmio on nimetty sen kärjensä mukaan. Esimerkiksi kuvan 2 vasemmalla puolella oleva kolmio on ABC -kolmio, ja oikealla oleva on kolmio a'b'c '.

Muita merkintöjä on myös mahdollista käyttää; Esimerkiksi kulma α kuviossa 2 on merkitty BAC: ksi. Huomaa, että kärjen kirjain menee keskelle ja kirjaimet kirjoitetaan vastakkaiseen suuntaan kelloneulojen kanssa.

Se voi palvella sinua: ongelman rajaaminen

Muina aikoina kehystelee aksentti kulman merkitsemiseksi:

Tai käytetään symbolia ∠, koska edellinen merkintä ei ehkä ole helppoa tulostettuna, jota seuraa kärkipistettä vastaava kirjain:

α = ∠A

Kolmiotyypit

Kolmioiden luokittelukriteerejä on useita. Tavallisin on luokitella ne sivujensa mittauksen tai heidän kulman mittauksen mukaan. Niiden sivujen mitat riippuen kolmiot voivat olla: scaleenit, samoitus tai tasapainot:

-Skaaleeni: Sen kolme puolta ovat erilaisia.

-Sammutus: Siinä on kaksi eri puolta ja yksi.

-Tasasivuinen: Kolme puolta ovat samat.

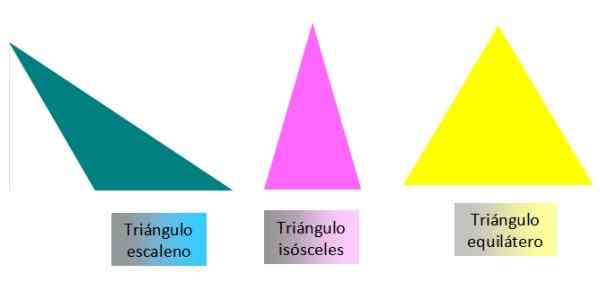Kuva 3. Kolmioiden luokittelu sivuillaan. Lähde: f. Zapata

Niiden kulmien mittauksen mukaan kolmioita kutsutaan seuraavasti:

-Tylppä, Jos yksi sisäkulmista on suurempi kuin 90º.

-Akuttaa, Kun kolmion kolme sisäkulmaa ovat akuutteja, ts. Alle 90º

-Suorakulmio, Siinä tapauksessa, että yksi sen sisäkulmista on 90º: n arvoinen. Sivuja, jotka muodostavat 90º.

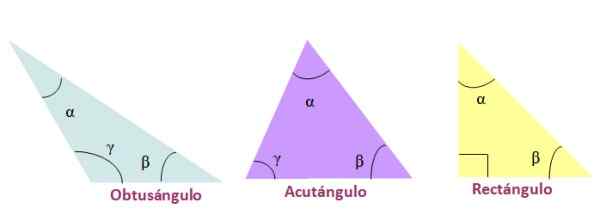Kuva 4. Kolmioiden luokittelu niiden sisäisten kulmien mukaan. Lähde: f. Zapata.

Kolmioiden yhtenäisyys

Kun kahdella kolmiolla on sama muoto ja ne ovat yhtä suuria, sanotaan, että ne ovat yhdenmukaisia. Kongruenssi liittyy tietysti tasa -arvoon, joten miksi geometriassa puhumme "kahdesta kongruentista kolmiosta" "kahden tasa -arvoisen kolmion" sijasta "?

No, on suositeltavaa käyttää termiä "kongruenssi" pysyäkseen totuuteen, koska kahdella kolmiolla voi olla sama muoto ja koko, mutta ne suuntautuvat eri tavalla tasossa (katso kuva 3). Geometrian kannalta ne eivät enää olisi tiukasti samoja.

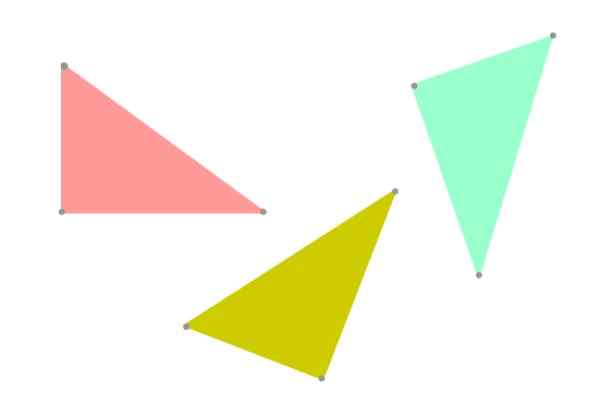Kuva 5. Yhteydet kolmiot, mutta ei välttämättä samat, koska sen suunta koneessa on erilainen. Lähde: f. Zapata.

Kongruenssikriteerit

Kaksi kolmiota ovat yhdenmukaisia, jos tapahtuu jokin seuraavista tilanteista:

-Kolme puolta mittaavat saman (jälleen tämä on ilmeisin).

-Heillä on kaksi identtistä puolta ja sama kulma niiden välillä.

-Molemmilla on kaksi identtistä sisäkulmaa ja näiden kulmien välinen puoli on sama.

Kuten voidaan nähdä, kyse on kahdesta kolmiosta, jotka täyttävät tarvittavat olosuhteet siten, että niiden rakennettaessa niiden muoto ja koko ovat täsmälleen samat.

Yhteyksiä koskevat kriteerit ovat erittäin hyödyllisiä, koska käytännössä lukemattomat mekaaniset osat ja osat on valmistettava sarjassa, joten niiden toimenpiteet ja muoto ovat täsmälleen samat.

Kolmioiden samankaltaisuus

Kolmio on samanlainen kuin toinen, jos niillä on sama muoto, vaikka ne olisivat erikokoisia. Jotta muoto on sama, vaaditaan, että sisäkulmilla on sama arvo ja sivut ovat verrannollisia.

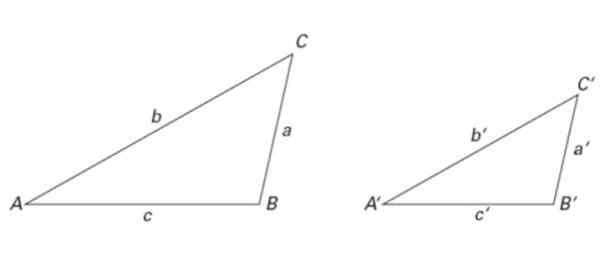Kuva 6. Kaksi samanlaista kolmiota: niiden koot eroavat toisistaan, mutta niiden mittasuhteet ovat samat. Lähde: f. Zapata.

Kuvan 2 kolmiot ovat myös samanlaisia, samoin kuin kuviossa 6. Täten:

∠ A = ∠ A ', ∠ B = ∠ B 'ja ∠ C = ∠ C '

Sivujen suhteen seuraavat samankaltaisuuden syyt täyttyvät:

a/a '= b/b' = c/c '

Ominaisuudet

Kolmioiden perusominaisuudet ovat seuraavat:

-Minkä tahansa kolmion sisäkulmien summa on aina 180º.

-Jokaiselle kolmiolle sen ulkoisten kulmien summa on yhtä suuri kuin 360 °.

Voi palvella sinua: Perustutkimus: Ominaisuudet, määritelmä, esimerkit

- Kolmion ulkoinen kulma on yhtä suuri kuin kahden sisäkulman summa, joka ei ole kyseisen kulman vieressä.

Lauseet

Ensimmäinen lause

Ne johtuvat kreikkalaisesta filosofista ja matemaatikoista tarinoista Miletusista, jotka kehittivät useita geometriaan liittyviä lauseita. Ensimmäinen heistä vahvistaa seuraavat:

Jos useat rinnakkaiset viivat leikkaavat kaksi poikittaista viivaa, ne määrittävät segmentit, jotka ovat verrannollisia.

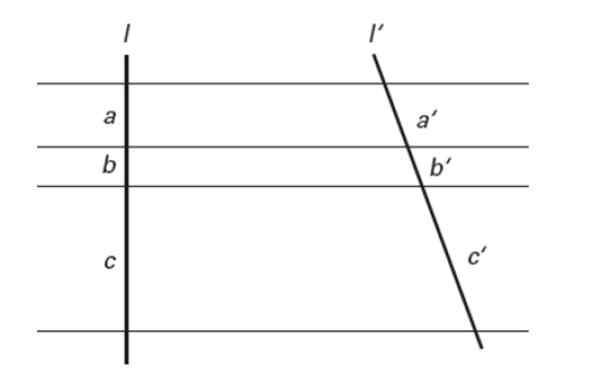Kuva 7. Tales -lause. Lähde: f. Zapata.

Toisin sanoen:

a/a '= b/b' = c/c '

Tällaisen ensimmäisen lauseen voidaan soveltaa kolmioon, esimerkiksi vasemmalla on ABC -sininen kolmio, jonka punaiset rinnakkaiset leikkaavat oikealle:

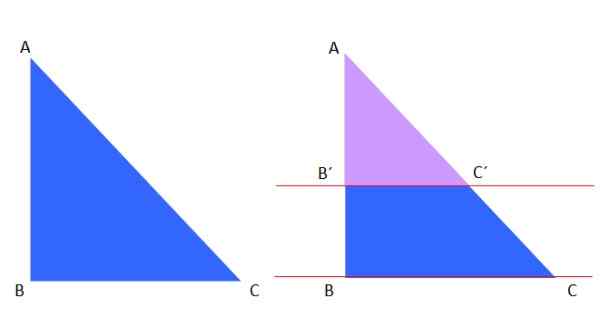Kuva 8. Sellaisten ja samanlaisten kolmioiden lause.

Violetin violetti kolmio on samanlainen kuin ABC -sininen kolmio, joten tällaisen lauseen mukaan seuraavat voidaan kirjoittaa:

Ab '/ac' = ab/ac

Ja se on yhdenmukainen sen kanssa, mitä edellä selitettiin kolmioiden samankaltaisuuden segmentissä. Muuten, yhdensuuntaiset viivat voivat olla myös pystysuuntaisia ​​tai yhdensuuntaisia ​​hypotenusen kanssa ja vastaavat kolmiot saadaan.

Tämän toisen lauseen

Tämä lause viittaa myös kolmioon ja keskikirjaan tai, kuten alla esitetyt. Tässä kuvassa AC on kehän halkaisija ja B on sen kohta, joka on B erilainen kuin A ja B.

Tällaisten valtioiden toinen lause, että:

AB- ja BC -segmenttien välinen kulma on aina 90º, joten ABC -kolmio on suorakulmio.

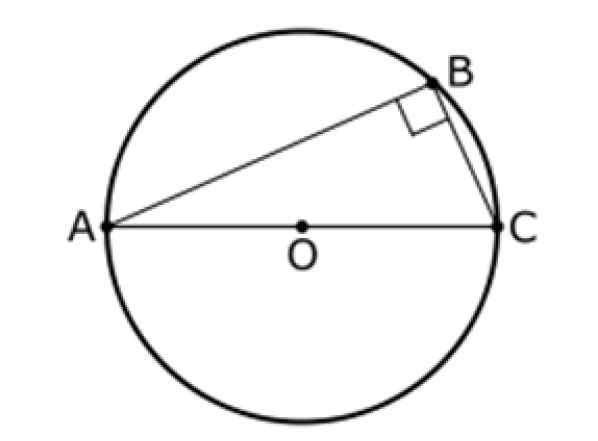Kuva 9. Tällaisen toinen lause. Lähde: Wikimedia Commons. Induktuniveload [julkinen alue].

Pythagoras -lause

Tämä on yksi historian tunnetuimmista lauseista. Se johtuu Samosin kreikkalaisesta matemaatikoista Pythagorasista (569 - 475. C.) ja sitä voidaan soveltaa oikeaan kolmioon. Sanoo niin:

Suorakulmion kolmiokategorioiden pituuksien neliöiden summa on yhtä suuri kuin hypotenuusin pituus korkealle neliölle.

Jos otamme esimerkiksi kuvan 8 sinisen kolmion tai violetin kolmion, koska molemmat ovat suorakulmioita, niin voidaan sanoa:

Ac² = AB² + BC² (Sininen kolmio)

Ac '² = Ab '² + Bc '² (Violetti kolmio)

Kolmion alue

Kolmion alue annetaan sen pohjan tuloksena -lla ja sen korkeus h, jaettuna 2: lla. Ja trigonometrialla tämä korkeus voidaan kirjoittaa H = b sinθ.

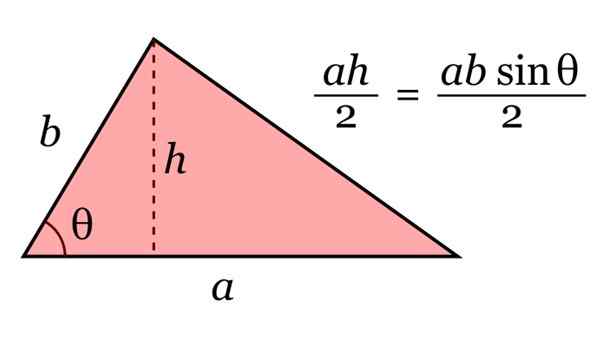Kuva 10. Kolmion alue. Lähde: Wikimedia Commons.

Esimerkkejä kolmioista

Esimerkki 1

Sanotaan maa.

Tämä on menettelyn kaavio, jota seuraa sellainen:

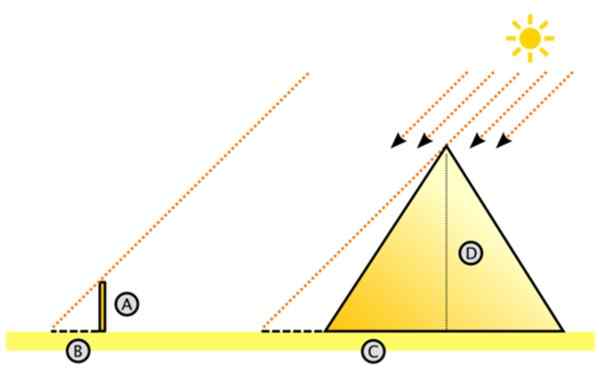Kuva 11. Kaavio suuren pyramidin korkeuden mittaamiseksi kolmioiden samankaltaisuudella. Lähde: Wikimedia Commons. Dake [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Sellainen perustellusti oletetaan, että auringonsäteet vaikuttavat rinnakkain. Tätä silmällä pitäen hän kuvitteli suuren oikean oikean kolmion.

Pyramidin korkeus ja C on etäisyys maassa, joka mitataan keskustasta varjoon, jonka pyramidi projisoi autiomaassa. Voi olla työlästä mitata C, mutta se on varmasti helpompaa kuin pyramidin korkeuden mittaaminen.

Vasemmalla puolella on pieni kolmio kissoista A ja B, missä A on vaarnan korkeus pystysuoraan lattialle ja B on sen projisointi. Molemmat pituudet ovat mitattavissa, aivan kuten C (C on yhtä suuri kuin pyramidin pituuden varjo + puoli).

Voi palvella sinua: Mitkä ovat tunto -ärsykkeet?

Sitten kolmioiden samankaltaisuudella:

A/b = d/c

Ja suuren pyramidin korkeus osoittautuu: D = C.(A/B)

Esimerkki 2

Siviilirakenteen panssari ovat rakenteita, jotka perustuvat ohuihin puun tai metallien suoriin tankoihin, joita käytetään tukena monissa rakennuksissa. Niitä tunnetaan myös nimellä hila, ristikko tai verkkovirta (Ristikko englanniksi).

Niissä kolmiot ovat aina läsnä, koska palkit on kytketty toisiinsa pisteisiin, joita kutsutaan solmuiksi, jotka voivat olla kiinteitä tai nivellettyjä.

Kuva 12. Kolmio on läsnä tämän sillan kehyksessä. Lähde: Pxhere.

Esimerkki 3

Triangulaationa kutsuttu menetelmä antaa sinun hankkia saavuttamattomien pisteiden sijainnin tuntemalla muut mitattavat etäisyydet, sillä ehdolla, että muodostuu kolmio, joka sisältää sen kärjen joukossa halutun sijainnin.

Esimerkiksi seuraavassa kuvassa haluat tietää missä vaiheessa meri on alus, nimeltään b.

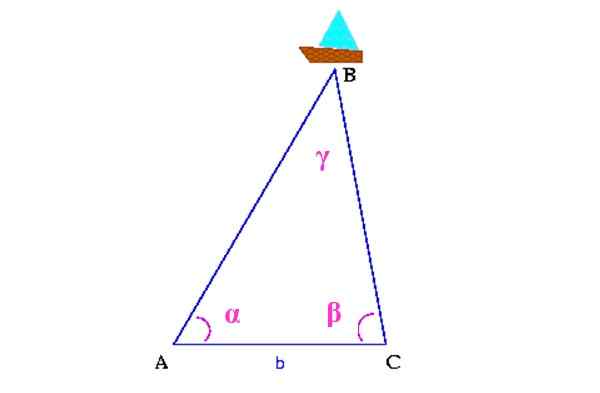Kuva 13. Triangulaatiojärjestelmä laivan löytämiseksi. Lähde: Wikimedia Commons. Colette [cc by-Sa 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Ensinnäkin mitataan kahden rannikon pisteen välinen etäisyys, joka kuvassa ovat A ja C. Sitten sinun on määritettävä kulmat α ja β a: n avulla theodoliitti, Laite, jonka tarkoituksena on mitata pystysuorat ja vaakasuorat kulmat.

Kaikilla näillä tiedoilla rakennetaan kolmio, jonka yläkärki on alus. Se vähentäisi kulmaa γ, keinoin.

Harjoitukset

Harjoitus 1

Kuvassa auringonsäteet ovat yhdensuuntaiset. Tällä tavalla 5 -metrin korkea puu projisoi 6 -metrin varjon maassa. Samanaikaisesti rakennuksen varjo on 40 metriä. Tällaisen lauseen jälkeen löydä rakennuksen korkeus.

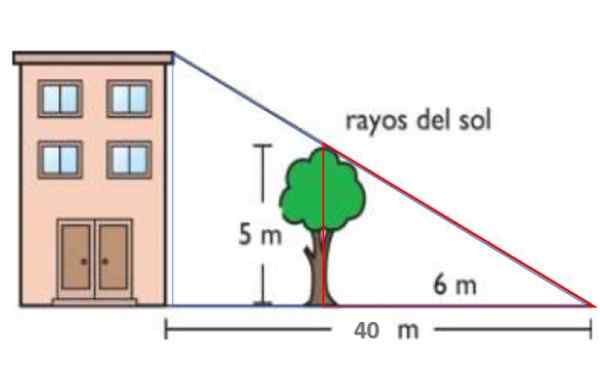Kuva 14. Vuoden järjestelmä ratkaistu 1. Lähde: f. Zapata.

Ratkaisu

Punaisen kolmion sivut ovat vastaavasti 5 ja 6 metriä, kun taas sinisellä on korkeus H -rakennus- ja pohjan korkeus 40 metriä. Molemmat kolmiot ovat siksi samanlaisia,:

H / 40 = 5/6 → H = 40.(5/6) M = 33.3 m

Harjoitus 2

Sinun on tiedettävä kahden pisteen välinen vaakasuuntainen etäisyys -Lla ja B -, Mutta ne sijaitsevat hyvin epäsäännöllisellä maastolla.

Suunnilleen keskipisteessä (P_m) Tästä maasta 1 näkyvyys erottuu.75 metriä korkea. Jos mittanauha osoittaa 26 metrin pituisen mitattuna A: sta näkyvyyteen ja 27 metrin päässä B: stä samaan pisteeseen, etsi etäisyys Ab.

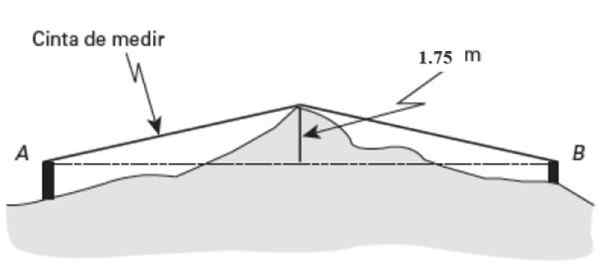Kuva 15. Harjoitusjärjestelmä ratkaistu 2. Lähde: Jiménez, R. Matematiikka II. Geometria ja trigonometria.

Ratkaisu

Pythagoras -lause on sovellettu kuvion kahteen suorakulmion kolmioon. Alkaen vasemmalla olevasta:

Hypotenuse = c = 26 metriä

Korkeus = A = 1.75 metriä

AP_m = (26² - 1.75²-A^1/2 = 25.94 m

Nyt Pythagorasia sovelletaan oikeaan kolmioon, tällä kertaa c = 27 metriä, a = 1.75 metriä. Näiden arvojen kanssa:

Bp_m= (27² - 1.75²-A^1/2 = 26.94 m

Etäisyys AB lisää nämä tulokset:

AB = 25.94 m +26.94 M = 52.88 m.

Viitteet

1. Baldor, J. -Lla. 1973.Litteä ja avaruusgeometria. Keski -Amerikan kulttuuri-.
2. Barredo, D. Kolmion geometria. Toipunut: Ficus.pntic.MEC.On.
3. Jiménez, r. 2010. Matematiikka II. Geometria ja trigonometria. Toinen painos. Pearson.
4. Wentworth, G. Planeetan geometria. Toipunut: Gutenberg.org.
5. Wikipedia. Kolmio. Palautettu: on. Wikipedia.org.