Täydellinen neliömäinen trinomiaalinen

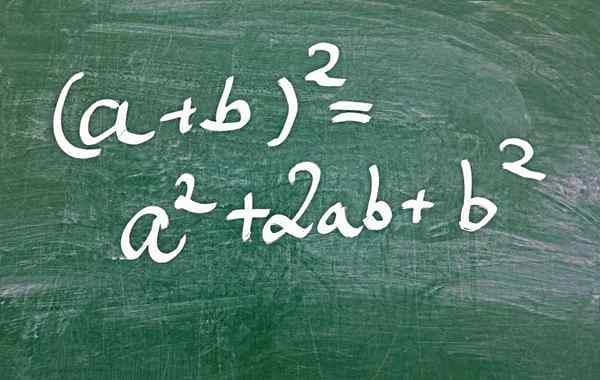Kuvio 1.- Yksi tapa saada täydellinen neliömäinen trinomi on summan neliön kautta

Mikä on täydellinen neliömäinen trinomi?

Täydellinen neliömäinen trinomial on, että kolmen termin polynomi, joista kaksi on täydellisiä neliöitä määristä A ja B ja niitä edeltää sama merkki, kun taas kolmas termi on täsmälleen A- ja B -tuote, joka pystyy olemaan Eri merkki.

Täydellinen neliömäinen trinomiaalinen saadaan neliömäisesti binomin ja algebran summa tai ero, sen muoto on seuraava:

-lla² ± 2 ∙ AB + B²

Kuten voidaan nähdä, täydellinen neliömäinen trinomial sisältää:

• Kaksi ei -samanlaista neliömäistä termiä, joita edeltää sama merkki: a² ja b²
• Kolmas termi 2 ∙ AB, joka on kvadraattisten termien neliöjuurten kaksoistuote ja jota voidaan edeltää positiivinen tai negatiivinen merkki.

Täydelliset neliömäiset trinomit voivat olla yksi tai useampi muuttuva. Esimerkiksi seuraava trinomiaalinen on täydellinen muuttujan neliö:

• x² + 6x + 9

Huomaa, että ensimmäiset termit (x²) ja kolmas (9) ovat vastaavasti neliömäisiä määriä, joita kutsutaan A ja B. Todellakin x² Se on x: n neliö ja 9 on 3 neliö. Tällä tavalla voit kirjoittaa seuraavan:

a = x

B = 3

Ja jäljellä oleva termi on x: n ja 3: n kaksinkertainen tuote:

6x = 2 ∙ 3 ​​∙ x

Kun varmennus on tehty, on varmaa, että tämä trinomiaalinen on täydellinen neliö.

Esimerkit

Kuva 2.- Esimerkkejä täydellisistä neliön trinomeista. Lähde: f. Zapata.

Täydelliset neliömäiset trinomit esiintyvät myös kahdessa tai useammassa muuttujassa, esimerkiksi:

4x² + 4xy + ja²

Se on trinomiaalinen kahdessa muuttujassa: "x" ja "y". Voidaan varmistaa, että se on täydellinen neliömäinen trinomiaalinen, koska se esittelee kaksi neliömäistä termiä:

4x² = (2x)²

ja² = (y)²

Ja jäljellä oleva termi on vastaavien neliöjuurten kaksoistuote: "2x" ja "y":

Voi palvella sinua: Orthoedro: kaavat, alue, tilavuus, diagonaali, esimerkkejä

4xy = 2 ∙ 2x ∙ ja

Tähän mennessä esitetyt trinomit ovat luokka 2 muuttujassa "x", mutta niiden ei välttämättä tarvitse olla tällaisia. Seuraava Trinomial on luokka 4 "X":

9x⁴ - 30x²Yz + 25y²z -z²

On helposti varmennettu, että tämä on täydellinen neliömäinen trinomi. Ensimmäinen termi on täydellinen 3x -neliö², Siitä lähtien (3x²-A² = 9x⁴.

Termi 25y²z -z² on yhtä suuri kuin (5yz)². Lopuksi jäljellä oleva termi on 2 ∙ 3x²∙ 5yz = 30 x²ja z.

Toisaalta alla esitetyt trinomit eivät ole täydellisiä neliömäisiä trinomeja:

• x²  + 8x - 16

Se ei ole täydellinen neliömäinen trinomia, koska 16, vaikka se on 4², Sitä edeltää negatiivinen merkki, kun taas toinen kvadraattinen termi (x²) on positiivinen.

• x²  - 15x + 25

Se ei ole myöskään täydellinen neliömäinen trinomia, koska vaikka sillä on kaksi neliömäistä termiä: x² ja 5², Termi 15x ei ole yhtä suuri kuin 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Tämä trinomiaalinen ei ole täydellinen neliö, koska se sisältää vain neliömäisen termin: 4x² = (2x)².

Eron summan ja neliön neliö

Täydelliset neliömäiset trinomit saadaan kehittämällä kahden tyyppisiä merkittäviä tuotteita:

• Summan neliö.
• Eron neliö.

Ensinnäkin kehitys saadaan jakautuvasta ominaisuudesta, koska neliön binomiaalisten keskiarvojen nostaminen kertoo sen itsensä kanssa:

(A ± B)² = (a ± b) × (a ± b) = a² ± A ∙ B ± B ∙ A + B² = a² ± 2A ∙ B + B²

Saatu trinomiaalinen on tulos, joka muistetaan vain pienellä harjoituksella ja on eräänlainen pikakuvake, joka helpottaa kehitystä, minkä vuoksi sitä kutsutaan merkittäväksi tuotteeksi.

Voi palvella sinua: Transcendent -numerot: Mitä ovat, kaavat, esimerkit, harjoitukset

Seuraavat trinomit saadaan helposti huomattavalla tuotteella ilman uudelleenhoitoa jakautuvaa ominaisuutta.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 ja² +20xy + 4x²

Täydellisen neliön trinomin tekijä

Usein ja välttämätön toiminta algebrassa on täydellisen neliömäisen trinomin tekijä, jonka kautta trinomi ilmaistaan ​​kahden termin summan tai vähentämisen neliönä (binomiaalinen).

Käänteinen toimenpide on merkittävän tuotteen kehittäminen, koska tuloksena oleva trinomiaalinen on ajatuksena saada binomiaalinen, joka aiheuttaa sen, kun se nousee 2: een.

Esimerkiksi aiemmin analysoidussa 4x Perfect Square Trinomial² + 4xy + ja², Mikä on binomiaalinen, että kun se on neliö, se antaa sinulle?

Neliömäisten termien vastaavat neliöjuuret ovat:

√ (4x²) = 2x

Joka vastaa: 4x² = (2x)²

√ (ja²) = y

Vastaa sitä sanomalla: ja² = (y)²

Siksi:

4x² + 4xy + ja² = (2x + y)²

Ja mikä on binomiaalinen⁴ - 30x²Yz + 25y²z -z²? Jälleen neliömäisten termien neliöjuuret uutetaan:

√ (9x⁴) = 3x²

√ (25 ja²z -z²) = 5yz

Niin:

(3x² - 5YZ)² = 9x⁴ - 30x²Yz + 25y²z -z²

Ratkaisut

Harjoitus 1

Suorita jokaisessa seuraavissa Trinomials -ohjelmassa tyhjä termi, josta puuttuu täydellinen neliömäinen trinomial:

olen² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Liittää jhk

Merkittävän tuotteen kaavan mukaan:

Voi palvella sinua: Täydentävät kulmat: mitkä ja miten ne lasketaan, esimerkkejä, harjoituksia

(A ± B)² = A² ± 2A ∙ B + B²

Trinomial:

m² + 18m + _____

Seuraa, että:

a = m (niin että² = m²-A

Lisäksi keskustermi on: 2 ∙ A ∙ B = 2M ∙ B = 18m, siksi b = 9 ja sen neliö on 9² = 81. Kaveri merkittävän tuotteen kaavan mukaan trinomial on tällainen:

(M + 9)² = M² + 18m + 81

• Ratkaisu b

Tässä trinomial:

4x² - _____ + 64

Voit tietää ja b:

A = √ (4x²) = 2x

B = √64 = 8

Siksi puuttuva termi on A: n ja B: n kaksinkertainen tuote:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

Ja haluttu trinomiaalinen on:

4x² - 32x + 64

• Liuos C

Trinomial:

_____ + 30n + 25

Ensimmäinen termi puuttuu, mutta tiedetään, että:

B = √25 = 5

JA

2 ∙ AB = 2 ∙ A ∙ 5 = 10A = 30N

Siksi a = 3N ja haluttu trinomiaalinen on:

9n² + 30n + 25

Harjoitus 2

Tarkista, että seuraava on täydellinen neliömäinen trinomiaali ja tekijä se:

16y² - 24yz + 9Z²

• Ratkaisu

Ensinnäkin on todistettu, että neliömäisiä termejä edeltää sama merkki ja sitten vastaavat neliöjuuret löytyvät:

A = √ (16y²) = 4y

B = √ (9Z²) = 3Z

Sitten sinun on tarkistettava, onko jäljellä oleva termi A: n ja B: n kaksinkertainen tuote:

2 ∙ AB = 2 ∙ 4Y ∙ 3Z = 24yz

Jos se on, niin trinomiaalista voi olla tekijä eron neliönä, koska keskustermiä edeltää negatiivinen merkki:

16y² - 24yz + 9Z² = (4y - 3z)²

Viitteet

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Katen matematiikan oppitunnit. Täydelliset neliömäiset trinomit. Toipunut: KatesMathlessons.com.
3. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
4. Zill, D. 2008. Ennakkoluulo laskenta etenee. Neljäs. Painos. McGraw Hill.