Absoluuttinen arvo

Mikä on absoluuttinen arvo?

Hän absoluuttinen arvo reaaliluku on määritelty etäisyytenä todellisen viivan määrän ja 0: n välillä. Etäisyyden vuoksi sen arvo on aina positiivinen tai nolla ja yhtä suuri kuin numeron luku.

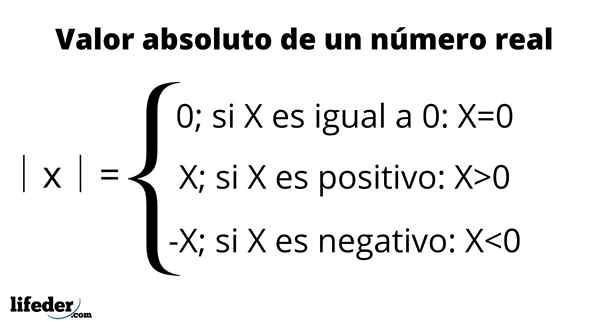
Absoluuttista arvoa esitetään asettamalla numero kahden pystysuoran palkin välillä, symboli, joka luetaan: "absoluuttinen arvo”, Kuten seuraavassa taulukossa on yhteenveto:

Esimerkiksi absoluuttinen arvo -3 on kirjoitettu │ -3│ ja on yhtä suuri kuin 3. Tämä tarkoittaa, että välillä -3 ja 0 on kolme yksikköä, mikä edustaa todellisen viivan numeroita. Toisaalta myös +3 tai yksinkertaisesti 3 absoluuttinen arvo on myös 3, koska mittaamalla sen etäisyys 0: een se on myös kolme yksikköä.

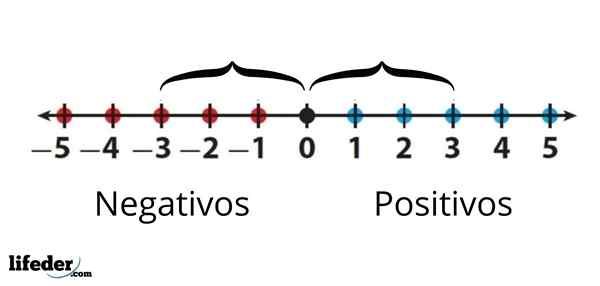Absoluuttinen arvo -3 on yhtä suuri kuin absoluuttinen arvo +3, koska jommankumman välillä 0 on sama on sama

Yhteenvetona voidaan todeta, että numeron absoluuttinen arvo on sama lukumäärä, mutta aina positiivinen merkki.

Absoluuttisen arvon ominaisuudet

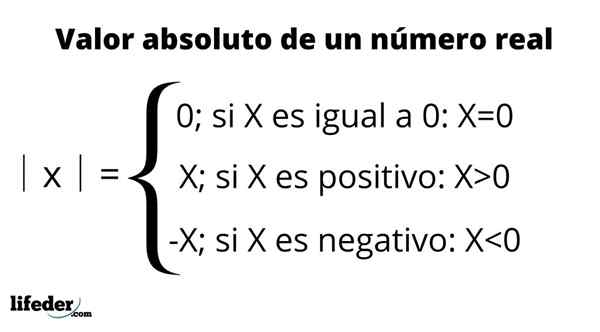Absoluuttisen arvon määritelmä

Absoluuttisen arvon pääominaisuudet:

• 1) numeron absoluuttinen arvo on aina positiivinen tai 0, siksi:

│X│ ≥ 0

• 2) nollan absoluuttinen arvo on myös nolla, eli │0│ = 0, siksi voidaan vahvistaa, että:

│x│ = 0, kyllä ​​y vain jos x = 0

• 3) Jokaiselle reaalilukujoukkoon kuuluvalle numerolle X on yhtä suuri kuin - x: x: x:

│X│ = │ - x│

• 4) Jos X -numeron absoluuttinen arvo on A, se tarkoittaa, että kyseiselle numerolle on kaksi vaihtoehtoa: i) x = +a tai ii) x = -a.

Se voi palvella sinua: Mary matkustaa 2/4 Cyclepististä, Melissa matkustaa 4/8 ja Anahi Travels 3/6

Esimerkiksi, jos numeron absoluuttinen arvo on 5, kaksi mahdollisuutta ovat, että numero on +5 tai -5.

Toiminnot, joilla on absoluuttinen arvo

Seuraavat ominaisuudet ovat erittäin hyödyllisiä absoluuttisten arvojen operaatioiden tekemiseen:

• 5) "X" ja "Y", jotka ovat kaksi todellista lukua, seuraava epätasa -arvo on aina toteutettu, nimeltään Absoluuttisen arvon kolmion muotoinen eriarvoisuus-

│x│+│y│≥ │x+y│

Esimerkiksi: ole:

x = -6

y = 9

Eriarvoisuuden vasen puoli on:

│-6│ + │9│ = 6 + 9 = 16

Ja oikea puoli on:

│-6+9│ = │3│ = 3

Ilmeisesti 16 on suurempi tai yhtä suuri kuin 3, ja näin on aina, kun numerot x ja ja niillä on erilaisia ​​merkkejä. Jos niillä on yhtä suuret merkit, tasa -arvo saadaan. Katso tämä toinen esimerkki kahden muun eri arvon kanssa:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

Todellakin:

8 = 8

• 6) Kahden reaalilukun "x" ja "y" vastaavien absoluuttisten arvojen tuote on yhtä suuri kuin numeroiden tuotteen absoluuttinen arvo:

│x│ ∙ │y│ = │x ∙ y│

Jälleen ovat arvot:

x = -6

y = 9

Niin:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Joka on yhtä suuri kuin:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) Kahden todellisen numeron "x" ja "y" absoluuttisen arvon absoluuttisen arvon jakaminen, jonka eri nimittäjä on 0, on näiden numeroiden välisen osuuden absoluuttinen arvo:

Niin kauan kuin ja ≠ 0.

Esimerkki:

Esimerkkejä absoluuttisesta arvosta

Yksinkertaiset esimerkit

Minkä tahansa reaalilukun absoluuttisen arvon laskeminen on hyvin yksinkertaista, esimerkiksi seuraavien numeroiden absoluuttinen arvo on:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Laskelmat, joissa on todellisen numeron absoluuttinen arvo

Suorita seuraavat toiminnot, joihin liittyy absoluuttinen arvo:

a) 2⋅│8│ + 5⋅│ -16│ -⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Voi palvella sinua: puolet 15: stä

Tämä on yhdistetty toimenpide, joten on edullista ratkaista se vaiheittain. Ensimmäinen absoluuttinen arvo on:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Toinen ilmestyvä absoluuttinen arvo lasketaan seuraavasti:

│81 ÷ (-3) │ = │-27│ = 27

Sitten saadut tulokset kerätään ja lopullinen laskelma suoritetaan:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19-6 + 27 = 40

Kahden pisteen välinen etäisyys todellisella viivalla

Absoluuttinen arvo näkyy monissa sovelluksissa, kuten etäisyyden löytäminen kahden todellisen linjan välillä. Jos A on todellinen numero, se sijaitsee oikealla linjalla siinä pisteessä, jonka abskissa on “A”, sama tapahtuu todellisen numeron B.

Anna "A" ja "B" kaksi numeroa oikealla viivalla, etäisyys, joka erottaa ne, on:

d -d_Ab = │b - a│

Joka voidaan myös laskea:

d -d_Ab = │a - b│

Esimerkiksi a = 5 ja b = 12: n välinen etäisyys on:

D = │5−12│ = │12−5│ = 7

Tällä tavoin kahden reaalilukun välisen vähennyksen absoluuttinen arvo on yksinkertaisesti etäisyys, joka erottaa ne oikealla viivalla.

Absoluuttinen arvon funktio

Absoluuttinen arvofunktio on sovellus, joka jatkuu reaaliluvujen sarjassa ℛ, kunnes ℛ⁺, joka vastaa kutakin reaalinumeroa sen absoluuttista arvoa. Se on määritelty:

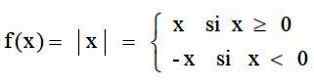
Ja sen kaaviossa on tyypillinen V -muoto:

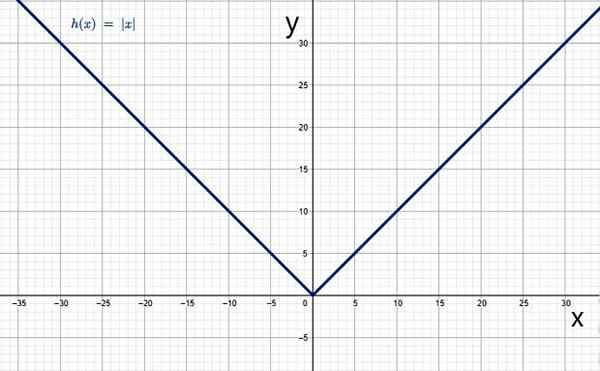Absoluuttinen arvo funktiona. Lähde: f. Zapata Geogebran kautta.

Absoluuttisen arvon ominaisuudet

-Verkkotunnuksesi on kaikkien todellisten lukujen sarja.

-Se on jatkuvaa.

-Se on jopa, koska on täytetty, että f (x) = f (-x), siksi pystysuora akseli on symmetria-akseli.

-Absoluuttisen arvofunktion alue on positiivisten todellisten joukkojen joukko, mukaan lukien 0, koska funktio edustaa aina etäisyyttä, ja tämä on aina positiivinen tai nolla.

Voi palvella sinua: mikä on ohje? (Geometria)

-Se on funktio osioiden tai osien mukaan.

-Vähenee aikavälillä (-∞, 0) ja kasvaa (0,+∞).

Absoluuttinen arvoargumentti voi olla myös neliömäinen tai muu funktio, esimerkiksi se voidaan määritellä:

• f (x) = │x²-5x+3│
• g (x) = │sen x│

Absoluuttinen arvo on vastuussa siitä, että ne ovat positiivisia argumentin kuvista, joilla on negatiivinen merkki.

Ratkaisut

Harjoitus 1

Arvioi seuraavat algebralliset lausekkeet absoluuttisella arvolla:

a) │2x -5│ + │ --x + 1│ x = 3

b) │ (x - 5) ÷ (x+4) │ x = −1: ssä

Liittää jhk

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Ratkaisu b

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Harjoitus 2

Mikä on arvojoukko, joka edustaa seuraavaa eriarvoisuutta?

│X│≤ 3

Ratkaisu

Epätasa -arvo edustaa kaikkia todellisia lukuja, joiden absoluuttinen arvo on pienempi tai yhtä suuri kuin 3, siksi se on kaikkien numeroiden välillä -3 ja +3, myös nämä.

Välimerkinnässä se pysyy:

[-3,3]

Harjoitus 3

Ratkaise seuraava yhtälö absoluuttisella arvolla:

│2x-1│ = 5

Ratkaisu 

Kuten aiemmin on todettu, yhtälön ratkaisemiseksi absoluuttisella arvolla on tarpeen ottaa huomioon kaksi vaihtoehtoa. Tarkoitan kyllä:

│f (x) │ = c

Niin:

1) f (x) = c

2) f (x) = -c

Siksi tällä yhtälöllä, jonka argumentti on lineaarinen, on kaksi ratkaisua:

Ensimmäinen ratkaisu

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Toinen ratkaisu

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Arvioitaessa x₁ = 3 tai x₂ = -2 Alkuperäisessä yhtälössä on saatava tasa -arvo, tällä tavalla varmistetaan, että saadut arvot ovat ehdotetun yhtälön ratkaisu. Todellakin:

│ (2⋅3) -1│ = │6-1│ = 5

Ja yrittäessään toisella vaihtoehdolla saadaan myös tasa -arvo:

│2⋅ (-2) -1│ = │-4-1│ = 5

Viitteet

1. Baldor, a. 2005. Algebra. Kulttuuriryhmä.
2. Larson, r. 2012. Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
3. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
4. Stewart, J. 2007. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.