Jatkuvat muuttuvat ominaisuudet, esimerkit ja harjoitukset

Se Jatkuva muuttuja Se voi viedä äärettömän määrän numeerisia arvoja kahden tietyn arvon välillä, vaikka nämä kaksi arvoa olisivat mielivaltaisesti lähellä. Niitä käytetään kuvaamaan mitattavissa olevia ominaisuuksia; esimerkiksi korkeus ja paino. Jatkuvan muuttujan ottamat arvot voivat olla rationaalisia lukuja, reaalilukuja tai kompleksinumeroita, vaikka tämä viimeinen tapaus on harvemmin tilastoissa. 

Jatkuvien muuttujien pääominaisuus on, että kahden rationaalisen tai todellisen arvon välillä voidaan aina löytää, ja toisen ja ensimmäisen välillä voi löytää toisen arvon ja niin toistaiseksi.

Kuvio 1. Käyrä edustaa jatkuvaa jakautumista ja palkit ovat hienovaraisia. Lähde: Pixabay

Oletetaan esimerkiksi, että painomuuttuja ryhmässä, jossa suurin paino on 95 kg ja alhaisin 48 kg: n paino; Se olisi muuttujan alue ja mahdollisten arvojen lukumäärä on ääretön.

Esimerkiksi välillä 50,00 kg - 50,10 kg voi olla 50,01. Mutta välillä 50,00–50,01 mitta voi olla 50 005. Se on jatkuva muuttuja. Toisaalta, jos mahdollisissa painossa mitataan yksi desimaalin tarkkuus, käytetty muuttuja olisi hienovarainen.

Jatkuvat muuttujat kuuluvat kvantitatiivisten muuttujien luokkaan, koska niillä on numeerinen arvo. Tällä numeerisella arvolla on mahdollista suorittaa matemaattisia operaatioita, jotka vaihtelevat aritmeettisesta äärettömän laskelman menetelmiin. 

[TOC]

Esimerkit

Suurin osa fysiikan muuttujista on jatkuvia muuttujia, niiden joukossa voimme nimetä: pituus, aika, nopeus, kiihtyvyys, energia, lämpötila ja muut.

Jatkuvat muuttujat ja erilliset muuttujat

Tilastoissa voidaan määritellä erityyppiset muuttujat, sekä laadulliset että kvantitatiiviset. Jatkuvat muuttujat kuuluvat tähän viimeiseen luokkaan. Heidän kanssaan on mahdollista suorittaa aritmeettiset ja laskentatoiminnot.

Esimerkiksi muuttuja h, Vastaa ihmisiä, joiden korkeus on välillä 1,50 - 1,95 m, se on jatkuva muuttuja. 

Vertaamme tätä muuttujaa tähän toiseen: kuinka monta kertaa on kallista valuutan käynnistämisessä, johon kutsumme n.

Muuttuja n Voit kuitenkin ottaa arvoja välillä 0 ja ääretön n Se ei ole jatkuva muuttuja, koska se ei voi ottaa arvoa 1,3 tai 1,5, koska arvojen 1 ja 2 välillä ei ole muuta. Tämä on esimerkki Erillinen muuttuja.

Jatkuvien muuttujien käyttö

Harkitse seuraavaa esimerkkiä: kone tuottaa fosforia vastaavia ja pakata ne laatikkoonsa. Määritetään kaksi tilastollista muuttujaa:

Voi palvella sinua: isobarinen prosessi: kaavat, yhtälöt, kokeet, harjoitukset

Muuttuja 1: L = Plose -pituus.

Muuttuja 2: n = sikojen lukumäärä laatikkoa kohden.

Nimellinen vastaa pituus on 5,0 cm 0,1 cm: n toleranssilla. Sikojen lukumäärä laatikkoa kohti on 50 ja toleranssi 3.

a) Ilmoita arvoalue, joka voi ottaa Lens ja N.

b) Kuinka monta arvoa voit ottaa Lens?

c) Kuinka monta arvoa voit ottaa n?

Sano kussakin tapauksessa, jos se on huomaamaton tai jatkuva muuttuja.

Ratkaisu

Arvot Lens Ne ymmärretään aikavälillä [5,0-0,1; 5,0+0,1]; toisin sanoen Lens on aikavälillä [4,9 cm; 5,1 cm] ja muuttuja Lens Voit ottaa äärettömät arvot näiden kahden mittauksen välillä. Se on sitten jatkuva muuttuja.

Muuttujan arvo n on aikavälillä [47; 53]. Muuttuja n Se voi viedä vain 6 mahdollista arvoa toleranssivälillä, se on silloin huomaamaton muuttuja.

Harjoittaa jtk todennäköisyysjakauma

Jos muuttujan ottamat arvot ovat jatkuvia, sen lisäksi Jatkuva satunnaismuuttuja. On erittäin tärkeää erottaa, onko muuttuja huomaamaton vai jatkuvaa, koska toisiinsa sovellettavat todennäköisyysmallit ovat erilaisia.

Jatkuva satunnaismuuttuja määritetään kokonaan, kun niiden olettavat arvot tunnetaan, ja todennäköisyys, että jokaisen niistä on tapahduttava.

-Todennäköisyydet 1

Matches -tehdas tekee niistä siten, että tikkujen pituus on aina välillä 4,9 cm - 5,1 cm ja nolla näistä arvoista. On todennäköistä saada sauva, joka mittaa välillä 5,00 - 5,05 cm, vaikka voisimme myös poimia yhden viidestä.0003 cm. Ovatko nämä arvot yhtä todennäköisiä?.

Voi palvella sinua: Suhteellinen tiheys: Laskenta, esimerkit, harjoitukset

Ratkaisu

Oletetaan, että todennäköisyystiheys on tasainen. Seuraavaksi luetellaan mahdollisuudet löytää fosfori tietyllä pituudella:

-Että fosfori on alueella [4,9; 5,1] on todennäköisyys = 1 (tai 100%), koska kone ei ota otteluita näistä arvoista.

-Fosforin löytäminen, joka on välillä 4,9 - 5,0, on todennäköisyys = ½ = 0,5 (50%), koska se on puolet pituuden alueesta.

-Ja todennäköisyys, että ottelun pituus on välillä 5,0 - 5,1, on myös 0,5 (50%)

-On tiedossa, että ei ole fosforikippuja, joiden pituus on välillä 5,0 - 5,2. Todennäköisyys: Nolla (0%).

Todennäköisyys löytää sauva tietylle alueelle

Tarkkailemme nyt seuraavia todennäköisyyksiä P saadaksesi tikkuja, joiden pituus on L: n välillä₁ ja minä₂-

 P = (l₂ -lens₁) /(L_Max - Lens_mini-A

-P, että ottelun pituus on välillä 5,00 - 5,05 P ([5.00; 5,05])-

P ([5.00; 5,05]) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P, että Cerrillon pituus on välillä 5,00 - 5,01, on:

P ([5.00; 5,01]) = (5,00 - 5,01)/(5,1 - 4,9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P, että Cerrillon pituus on välillä 5000 - 5 001 on vielä pienempi:

P (5000; 5 001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Jos jatkamme välein lähestymistä yhä enemmän 5,00: een, todennäköisyys, että sauvalla on tarkalleen 5,00 cm, on nolla (0%). Meillä on todennäköisyys löytää ottelu tietylle alueelle.

Todennäköisyys löytää useita sauvoja tietylle alueelle

Jos tapahtumat ovat riippumattomia, todennäköisyys, että kaksi tikkua ovat tietyllä alueella, on niiden todennäköisyyksien tuote.

-Todennäköisyys, että kaksi tikkua on välillä 5,0 - 5,1, on 0,5*0,5 = 0,25 (0,25%)

-Todennäköisyys, että 50 sauva on välillä 5,0-5,1, on (0,5)^50 = 9 × 10^-16, se on melkein nolla.

-Todennäköisyys, että 50 sauva on välillä 4,9 - 5,1, on (1)^50 = 1 (100%)

-Harjoitus 2 todennäköisyyksiä

Edellisessä esimerkissä tehtiin oletus, että todennäköisyys on tasainen tietyllä aikavälillä, mutta se ei aina ole.

Voi palvella sinua: hydrostaattinen paine: kaava, laskenta, esimerkit, harjoitukset

Todellisen koneessa, joka tuottaa tikkuja, mahdollisuus, että sauva on keskeisessä arvossa, on suurempi kuin yhdessä äärimmäisissä arvoissa. Matemaattisesta näkökulmasta tämä on mallinnettu funktiolla F (x), joka tunnetaan todennäköisyystiheytenä.

Todennäköisyys, että mitta on A: n ja B: n välillä. 

Oletetaan esimerkiksi, että haluamme löytää funktion f (x), joka edustaa yhdenmukaista jakautumista arvojen 4 4,9 ja 5.1 välillä. 

Jos todennäköisyysjakauma on tasainen, niin f (x) on yhtä suuri kuin vakio C, joka määritetään ottaen integraalin välillä 4,9 - 5,1. Koska tämä integraali on todennäköisyys, niin tuloksen on oltava 1.

Kuva 2. Tasainen todennäköisyystiheys. (Oma yksityiskohta)

Mikä tarkoittaa, että C on arvoinen 1/0,2 = 5. Toisin sanoen yhtenäinen todennäköisyystiheysfunktio on f (x) = 5, jos 4,9≤x≤5,1 ja 0 tästä alueesta. Kuvio 2 näyttää tasaisen todennäköisyystiheysfunktion.

Huomaa kuten saman leveyden välein (esimerkiksi 0,02), todennäköisyys on sama keskellä kuin jatkuvan muuttujan alueen lopussa Lens (Suolakurkun pituus).

Realistisempi malli olisi todennäköisyystiheysfunktio seuraavana:

-f (x) = -750 ((x-5,0)^2-0,01), jos 4,9≤x≤5,1

-0 Tämän alueen ulkopuolella 

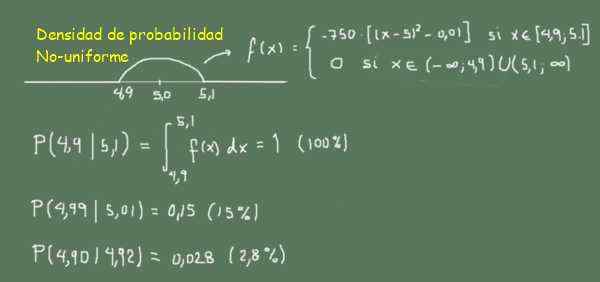Kuva 3. Ei -epätodennäköisyystiheysfunktio. (Oma yksityiskohta)

Kuviossa 3 sitä voidaan havaita, koska sauvojen löytämisen todennäköisyys välillä 4,99 - 5,01 (leveys 0,02) on suurempi kuin tikkujen löytäminen välillä 4,90 - 4,92 (leveys 0,02)

Viitteet

1. Dinov, Ivo. Erilliset satunnaismuuttujat ja todennäköisyysjakaumat. Palautettu: stat.UCLA.Edu
2. Erilliset ja jatkuvat satunnaismuuttujat. Palautettu: OCW.mittaa.Edu
3. Erilliset satunnaismuuttujat ja todennäköisyysjakaumat. Toipunut: kotisivu.DDMS.Uiowa.Edu
4. H. Peshro. Johdanto todennäköisyyteen. Palautettu: todennäköisyyskurssi.com
5. Mendenhall, W. 1978. Hallinnon ja taloustieteen tilastot. Ibero -meralainen toimitusryhmä. 103-106.
6. Satunnaismuuttujaongelmat ja todennäköisyysmallit. Palautettu: ugr.On.
7. Wikipedia. Jatkuva muuttuja. Toipunut Wikipediasta.com
8. Wikipedia. Tilastollinen muuttuja. Toipunut Wikipediasta.com.