Matematiikka

Suhteellinen vaihtelu

Suhteellinen vaihtelu

Mikä on suhteellista vaihtelua?

Kahden muuttujan "x" ja "y" välinen suhteellinen variaatio tapahtuu, kun kertomalla yksi niistä yhdellä vakiona, toinen myös kerrotaan tai jaetaan samalla vakiona. Monet todellisen maailman tilanteet voidaan kuvata oikein niiden kanssa.

Muuttujien välinen suhteellisuus voi olla suora tai käänteinen. Suorassa suhteellisuudessa suhde on tyyppinen:

y = k ∙ x

Tai vastaavasti:

K = y/x

Missä k on vakio nimeltään suhteellisuusvakio jompikumpi suhteellisuus. Huomaa, että jos "X" kasvaa, "Y" tekee sen samassa osassa ja jos "x" pienenee, se myös "y". Kun muuttujien välinen suhde on kuvaajia, saadaan suora viiva, joka kulkee koordinaattijärjestelmän alkuperän läpi (katso harjoitus ratkaistaan ​​myöhemmin).

Suora variaatio voi tapahtua myös yhden muuttujan ja toisen voiman välillä, esimerkiksi "Y" voi olla suoraan verrannollinen X: ään2, x3 ja niin.

Toisaalta käänteisessä suhteellisuudessa muuttujat on kytketty lausekkeen kautta:

x ∙ y = k

Tämä lauseke tarkoittaa, että muuttujien tuote on vakio. Muuttujien välinen suhde on hyperbola. Lisäksi, jos muuttujan tuote, jolla on toinen voima, on vakio, se edustaa myös tapausta, jolla on käänteinen suhteellisuus: esimerkiksi:

x2∙ y = k; x3∙ y = k ..

Esimerkit

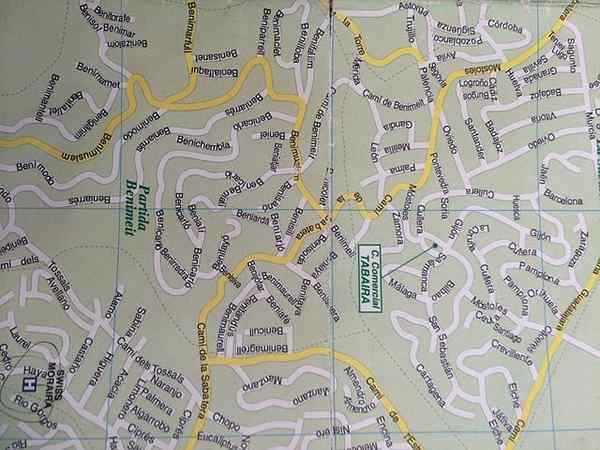Suhteellisen variaation soveltaminen on karttojen asettelu

Monet fysiikan ja kemian lait ilmaistaan ​​matemaattisesti mittasuhteina. Esimerkiksi jousen ja saman pidentymisen aiheuttama voima, paineen ja kaasun tilavuuden välinen suhde vakiolämpötilassa, yksinkertaisen heilurin ja sen pituuden ja monien muiden neliöjuuren ajanjakso. Kun tiedät ilmiötä hallitsevan mallin, voit selvittää käyttäytymisesi muuttujien minkä tahansa arvon suhteen.

Voi palvella sinua: olemassaolo ja ainutlaatuisuus lause: esittely, esimerkit ja harjoitukset

Ja paitsi, että niitä sovelletaan myös lukemattomiin tilanteisiin tällaisia:

  • Siirrä pienemmän kokoisen vaatteen kuvio suurempaan kokoon (tai päinvastoin).
  • Muuntamistekijöissä siirtyä yksiköstä toiseen, kuten kilometriä mailiin, gallonia litroihin ja paljon muuta.
  • Laske reseptin ainesosat 6 henkilölle, jotka tietävät vaatimuksen 4 ihmiselle.
  • Määritä tiettyjen verojen määrä saatujen tulojen mukaisesti.
  • Yksinkertaisen kiinnostuksen laskennassa.
  • Kun piirtävät tasoja mittakaavalle.
  • Kun sinun on laskettava tuotteen määrän hinta, joka tietää yksikön hinnan.
  • Kolmioiden samankaltaisuudessa.

Seuraavaksi yksityiskohtaisesti on kaksi mielenkiintoista tilannetta, joissa sovelletaan suhteellisia variaatioita:

Esimerkki 1

Hermitage Avenue mittaa 3 kaupungin mittakaavassa 3.2 cm, se on sen todellinen pituus 400 metriä. Toisaalta La Fuenten kadun, joka todella mittaa 180 m pitkään, on piirrettävä suhteellisesti lyhyemmällä iskulla. Mikä on aivohalvauksen koko?

Lausunto tarjoaa Ermita Avenuen täydelliset tiedot: Olkoon keinon todellinen pituus ja ℓ sen pituus koneessa, koska variaatio on suora suhteellisuus, sen on:

L = k ∙ ℓ

Hermitage Avenuen tiedoista voit tietää suhteellisuusvakion k: n arvon, mutta ennen kuin kaikki pituudet on jätettävä samoihin yksiköihin:

3.2 cm = 0.032 m

Niin:

400 m = k ∙ 0.032 m

Siksi suhteellisuusvakio on:

Voi palvella sinua: mitkä ovat vertauksen elementit? (Osat)

K = 400/0.032 = 12500

Nyt tiedetään, että:

L = 12500 ∙ ℓ

Tämä tulos tulkitaan seuraavasti: Katujen pituus tällä kartalla on 12500 kertaa pienempi kuin sen todellinen pituus. Siksi La Fuenten kadun linja mittaa:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Esimerkki 2

Analyytikolla on seuraavat kokeellisesti saadut muuttujien "x" ja "y" -arvotaulukon ja haluavat tietää, sopivatko nämä tiedot suoran suhteellisen variaation malliin vai yhden käänteisen suhteellisen variaation malliin.

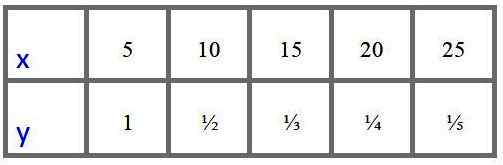
Mitä sinun pitäisi tehdä tietääksesi?

Ensinnäkin havaitaan, että kun “X” kasvaa, “Y” pienenee, joten se epäilee käänteistä suhteellisuutta, joka tapauksessa, analyytikolla on mahdollisuus arvioida, onko osamäärä ja/x vakio (suhteellinen variaatio suoraan) tai jos tuote x.ja on vakio (käänteinen suhteellinen variaatio).

Testaus ensimmäisellä vaihtoehdolla:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Johtopäätöksenä on, että se ei ole suora suhteellinen variaatio, koska osamäärä ja/x antaa erilaisia ​​arvoja jokaiselle parille tiedoille.

Meidän on tarkistettava, onko tuote x ∙ vakio:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Ja kun tuote x ∙ y = 5 päätellään, että variaatio on käänteistä suhteellisuutta.

Tämän tiedon on tiedettävä arvot, jotka eivät ole taulukossa, esimerkiksi mikä olisi ”y” -arvo, kun x = 30?

X ∙ Y = 5: stä ”Y” puhdistetaan ja korvataan x = 30:

y = 5/x

y = 5/30 = 1/6

Liikuntaa

Jos kangasmittari maksaa 6.75 dollaria, ja tietäen, että hinta on suoraan verrannollinen ostamaan metrien määrään, etsi:

Se voi palvella sinua: Antidervative: Kaavat ja yhtälöt, esimerkit, harjoitukset

a) Algebrallinen lauseke, joka yhdistää muuttujat "hinnan arvoon" ja "metrin määrän kangasta".

b) Valmistele arvotaulukko hinnoilla 3, 6, 9, 12, 15 ja 18 metriä kangasta.

c) Kaavio saadut arvot.

Vastaa

Anna "y" muuttujan "hinta $" ja "x" muuttuja "kankaan mittarit". Kuten suoraan suhteessa, sinun on:

y = k ∙ x

X = 1 metrille y = 6.75 dollaria, siksi k = 6.75 dollaria/metri. Tämä on kankaan yksikköhinta, minkä tahansa muun "X" -kankaan hinta saadaan kertomalla tällä arvolla, sitten haettu algebrallinen lauseke on:

y = 6.75 ∙ x

Vastaus b

Arvotaulukko, jonka hinnat ovat 3, 6, 9, 12, 15 ja 18 metriä, on:

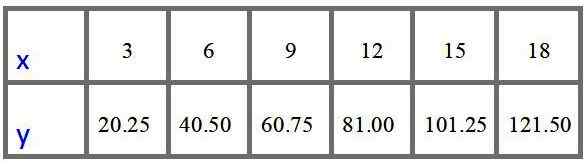
Vastaus C

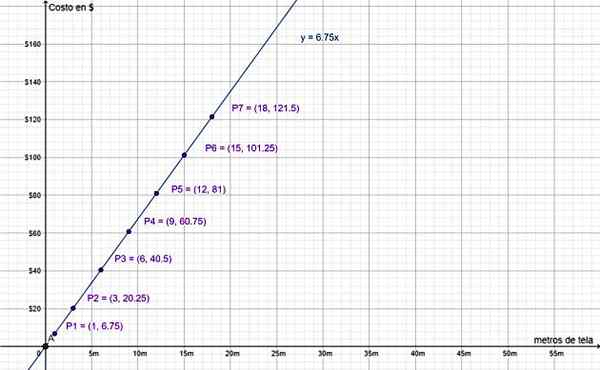
Lopuksi edellisen taulukon arvojen kaavio vahvistaa, että se on suora suhteellinen variaatio:

Kustannukset dollaria ja metrien määrää kangasta ovat suoraan verrannollisia määriä. Lähde: f. Zapata.

Huomaa, että arvo (0,0) sisältyy, koska rivi y = 6.75 ∙ x kulkee koordinaattijärjestelmän alkuperän läpi, kuten aiemmin selitettiin. On järkevää, koska ostoksen tekemättä jättäminen vastaa 0 m kankaan ostamista, jonka arvo on 0 $.

Viitteet

  1. Larson, r. 2012. Esikytkestys. Kahdeksas. Painos. Cengage -oppiminen.
  2. Meksikon julkisen koulutuksen sihteeristö. Suhteellinen vaihtelu. Haettu: PPS.K12.Tai.meille.
  3. Stewart, J. 2007. Pre-laskenta: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
  4. Yksinäinen. Opintooppaat: matematiikka i. Palautettu: Dirre.Yksinäinen.MX.
  5. Zill, D. 2008. Kalsukulutus laskelman edistyessä. Neljäs. Painos. McGraw Hill.