Vektoriominaisuudet ja ominaisuudet, elementit, tyypit, esimerkit

Se vektorit Ne ovat matemaattisia kokonaisuuksia, joilla on suuruuspositiivinen -yleensä mittayksikkö, suuntaa ja merkitystä lisäksi. Tällaiset ominaisuudet ovat erittäin tarkoituksenmukaisia ​​kuvaamaan fyysisiä määriä, kuten nopeutta, voimaa, kiihtyvyyttä ja monia muita.

Vektorien kanssa on mahdollista suorittaa toimintoja, kuten summa, vähennys ja tuotteet. Jakautumista ei ole määritelty vektoreille, ja tuotteen suhteen on olemassa kolme luokkaa, joita kuvaamme myöhemmin: skalaari- tai pistetuote, vektori tai ristituote ja skalaarin tuote vektorille.

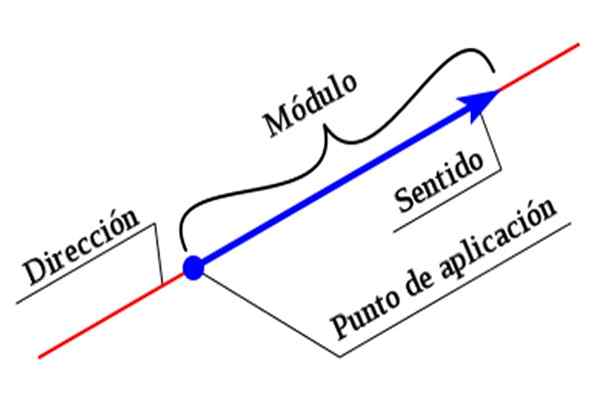Kuvio 1. Vektorin elementit. Lähde: Wikimedia Commons.

Vektorin kuvaamiseksi on välttämätöntä osoittaa kaikki sen ominaisuudet. Suuruus tai moduuli on numeerinen arvo, johon liittyy yksikkö, kun taas suunta ja merkitys perustetaan koordinaattijärjestelmän avulla.

Katsotaanpa esimerkkiä: Oletetaan, että lentokone lentää kaupungista toiseen nopeudella 850 km/h suuntaan. Tässä meillä on täysin määritelty vektori, koska suuruus on saatavana: 850 km/h, kun taas suunta ja merkitys ovat NE.

Vektorit esitetään yleensä graafisesti suuntautuneilla linjasegmenteillä, joiden pituus on verrannollinen suuruuteen.

Suunta ja merkityksen määrittämiseksi vaaditaan referenssiviiva, joka on yleensä vaakasuora akseli, vaikka pohjoista voidaan myös pitää referenssinä, kuten tason nopeus:

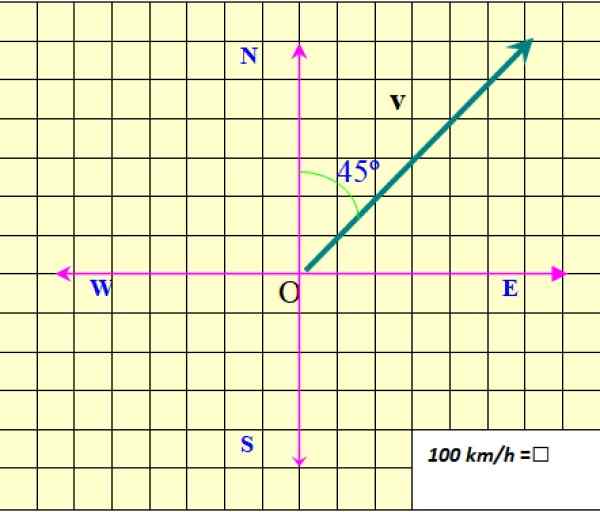Kuva 2. Nopeusvektori. Lähde: f. Zapata.

Kuva näyttää tason nopeusvektorin, joka on merkitty v sisään lihavoitu, Sen erottaminen skalaarisesta määrästä, joka vaatii vain numeerisen arvon ja jonkin määritettävän yksikön.

[TOC]

Vektorin elementit

Kuten olemme sanoneet, vektorielementit ovat:

-Voimakkuus tai moduuli, jota joskus kutsutaan myös absoluuttiseksi arvoksi tai vektoristandardiksi.

-Osoite

-Aisti

Kuvion 2 esimerkissä moduuli v Se on 850 km/h. Moduuli on merkitty V: ksi ilman rohkeaa tai |v|, Missä palkit edustavat absoluuttista arvoa.

Osoite v on määritelty pohjoiseen. Tässä tapauksessa se on 45º itään pohjoiseen (45º NE). Lopuksi nuolen kärki ilmoittaa v.

Tässä esimerkissä vektorialue on piirretty samaan aikaan lähtö- tai koordinaattijärjestelmän kanssa, tämä tunnetaan nimellä Linkitetty vektori. Toisaalta, jos vektorin alkuperä ei vastaa vertailujärjestelmän alkuperää, sanotaan, että se on a ilmainen vektori.

On huomattava, että vektorin täysin määrittämiseksi nämä kolme elementtiä on ilmoitettava, muuten vektorin kuvaus olisi epätäydellinen.

Vektorin suorakulmaiset komponentit

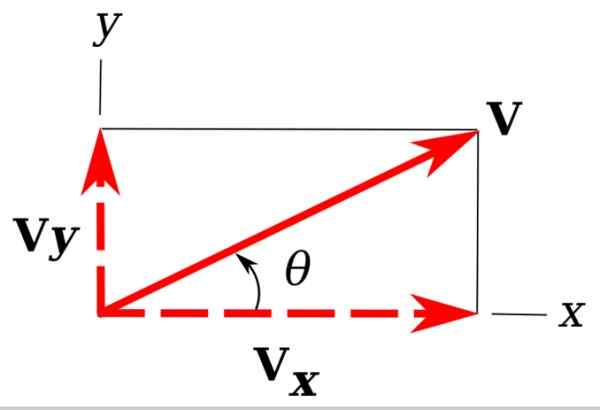Kuva 3. Tasossa olevan vektorin suorakulmaiset komponentit. Lähde: Wikimedia Commons. Unther [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Kuvassa meillä on esimerkkivektorimme takaisin v, se on koneessa Xy.

On helppo huomata, että X- ja Y -koordinaattiakselien V -projektiot määrittävät oikean kolmion. Nämä ennusteet ovat v_ja ja v_x ja niitä kutsutaan suorakulmaisista komponenteista v.

Tapa osoittaa v Suorakulmaisten komponenttien kautta se on tällainen: v = x, v_ja-. Näitä neliöhakeita käytetään sulujen sijasta korostaakseen sitä tosiasiaa, että se on vektori eikä piste, koska tässä tapauksessa suluja käytetään.

Voi palvella sinua: James Chadwick: Biography, Atomic -malli, kokeet

Jos vektori on kolmen ulottuvuuden tilassa, tarvitaan vielä yksi komponentti, niin että:

v = x, v_ja, v_{z -z}-

Tietäen suorakaiteen muotoiset komponentit, vektorin suuruus lasketaan, mikä vastaa oikean kolmion hypoteniuksen löytämistä, jonka jalat ovat v_x ja v_ja,. Pythagoras -lauseen kautta seuraa, että:

JavJa² = (v_x-A² +  (V_ja-A²

Vektorin polaarinen muoto

Kun vektorin suuruus tunnetaan JavJa Ja kulma θ, että tämä muoto referenssiakselilla, yleensä vaaka -akselilla, vektori on yhtä määritelty. Sitten sanotaan, että vektori ilmaistaan ​​polaarisessa muodossa.

Suorakulmaiset komponentit lasketaan helposti:

v_x = |vJa.cos θ

v_ja = |vJa.synti θ

Edellä esitetyn mukaan nopeusvektorin suorakaiteen muotoiset komponentit v lentokoneen olisi:

v_x = 850 . cos 45º km/h = 601.04 km/h

v_ja = 850 . Sen 45º km/h = 601.04 km/h

Kaverit

On olemassa erityyppisiä vektoreita. Siellä on Veine -vektoreita, sijainti, siirtymä, voima, sähkökenttä, liikkeen määrä ja monet muut. Kuten olemme jo sanoneet, fysiikassa on paljon vektorialueita.

Mitä vektoreihin, joilla on tiettyjä ominaisuuksia, voimme mainita seuraavat vektorit:

-Tyhjä: Nämä ovat vektoreita, joiden suuruus on 0 ja jotka on merkitty 0 -. Muista, että lihavoitu kirje symboloi vektorin kolmea perusominaisuutta, kun taas normaali kirjain edustaa vain moduulia.

Esimerkiksi staattisen tasapainon kehosta, voimien summan on oltava nollavektori.

-Ilmainen ja linkitetty: Vapaat vektorit ovat niitä, joiden alkuperä- ja.

Parin voiman tuottama pari tai hetki on hyvä esimerkki vapaasta vektorista, koska vääntömomentti ei koske tiettyä pistettä.

-Laitteet: Ne ovat kaksi ilmaista vektoria, joilla on identtiset ominaisuudet. Siksi heillä on sama suuruus, suunta ja merkitys.

-Coplanares tai koplanariot: Vektorit, jotka kuuluvat samaan tasoon.

-Vastakkaiset: vektorit, joilla on yhtä suuruus ja suunta, mutta vastakkaiset aistit. Vektori vastustaa vektoria v Se on vektori -v Ja molempien summa on nollavektori: v + (-v) = 0 -.

-Samanaikainen: vektorit, joiden toimintaviivat kaikki kulkevat saman pisteen läpi.

-Liukua: Ovatko vektorit, joiden levityspiste voi liukua tiettyä riviä pitkin.

-Kolineaali: Vektorit, jotka sijaitsevat samalla linjalla.

-Unakriitit: Ne vektorit, joiden moduuli on 1.

Ortogonaaliset yksikkövektorit

Fysiikan vektorityyppi on erittäin hyödyllinen, nimeltään Ortogonaal Unit Vektor. Ortogonaalisen yksikön vektorilla on moduuli yhtä suuri kuin 1 ja yksiköt voivat olla mikä tahansa, esimerkiksi nopeuden, aseman, lujuuden tai muun kanssa.

On joukko erityisiä vektoreita, jotka auttavat helposti edustamaan muita vektoreita ja suorittamaan operaatioita heidän kanssaan: ne ovat ortogonaalisia yksikkövektoreita Yllyttää, J - ja k -k -, Unitarit ja kohtisuora toisiinsa nähden.

Kahdessa ulottuvuudessa nämä vektorit on suunnattu molempien akselin positiiviseen merkitykseen x akselista ja. Ja kolmiulotteisesti yksikkövektori lisätään akselin suuntaan z -z positiivinen. Ne on esitetty seuraavasti:

Voi palvella sinua: mikä on dokumenttitutkimuksen rakenne?

Yllyttää =

J - =

k -k - =

Yksikkövektorit voivat edustaa vektoria Yllyttää, J - ja k -k - seuraavasti:

v = v_x Yllyttää + v_ja J - + v_{z -z} k -k -

Esimerkiksi nopeusvektori v Edellisistä esimerkeistä voit kirjoittaa seuraavasti:

v = 601.04 Yllyttää + 601.04 J - km/h

Komponentti k -k - Se ei ole välttämätöntä, koska tämä vektori on tasossa.

Vektorien summa

Vektorien summa esiintyy hyvin usein erilaisissa tilanteissa, esimerkiksi kun haluat löytää tuloksena olevan voiman esineestä, johon erilaiset voimat vaikuttavat. Aloita olettaa, että sinulla on kaksi ilmaista vektoria tai ja v Koneessa, kuten seuraava näyttää vasemman:

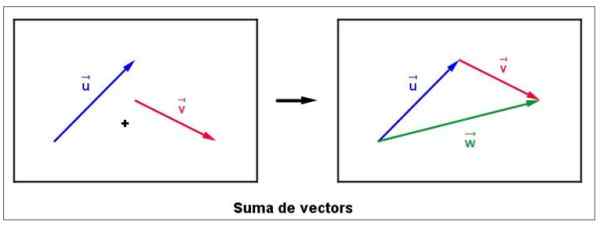Kuva 4. Kahden vektorin graafinen summa. Lähde: Wikimedia Commons. LLUC Cabanach [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Hän siirtyy heti vektoriin v, muuttamatta sen suuruutta, suuntaa tai merkitystä, niin että se on peräisin samaan aikaan tai.

Summavektoria kutsutaan W - ja vedetään alkaen U: sta v, Oikean luvun mukaan. On tärkeää huomata, että vektorin suuruus W - Se ei välttämättä ole v ja tai.

Jos se heijastuu huolellisesti tältä osin, ainoa tapaus, kun tuloksena olevan vektorin suuruus on lisäysten suuruuksien summa, se on silloin, kun molemmat addiktit ovat samaan suuntaan ja niillä on sama merkitys.

Ja mitä tapahtuu, jos vektorit eivät ole ilmaisia? Ne on myös erittäin helppo lisätä. Tapa tehdä on komponentin komponentin tai analyyttisen menetelmän lisääminen.

Tarkastellaan esimerkiksi seuraavan kuvan vektoreita, ensin on ilmaista ne yhdestä aiemmin selitetystä Cartesian muodoista:

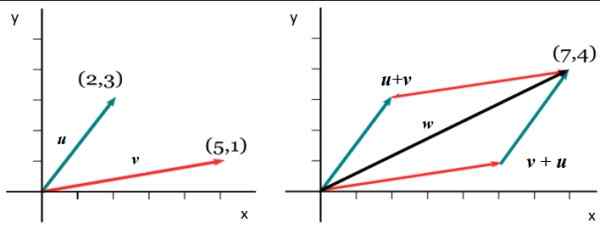Kuva 5. Kahden kytketön vektorin summa. Lähde: Wikimedia Commons.

v =

tai =

Komponentin saamiseksi x vektorista lisää W -, Vastaavat komponentit lisätään x - v ja tai- W -_x = 5+2 = 7. Ja saada W -_ja Noudatetaan analogista menettelyä: w_ja = 1+3. Siksi:

tai =

Vektorien summan ominaisuudet

-Kahden tai useamman vektorin summa johtaa toiseen vektoriin.

-Se on kommutatiivista, lisäysten järjestys ei muuta summaa, joten:

tai + v = v + tai

-Vektorien summan neutraali elementti on nollavektori: v + 0 - = v

-Kahden vektorin vähentäminen määritellään päinvastaisen summana: v - u = v + (-tai)

Esimerkkejä vektoreista

Kuten olemme sanoneet, fysiikassa on lukuisia vektorimääriä. Tunnetuimpia ovat:

-Sijainti

-Siirtymä

-Keskimääräinen nopeus ja hetkellinen nopeus

-Kiihtyvyys

-Pakottaa

-Liikkeen määrä

-Vääntömomentti tai voimamomentti

-Impulssi

-sähkökenttä

-Magneettikenttä

-Magneettinen hetki

Toisaalta he eivät ole vektoreita, vaan kiipeily:

-Aika

-Massa

-Lämpötila

-Tilavuus

-Tiheys

-Mekaaninen työ

-Energia

-Lämmitys

-Voima

-Jännite

-Sähkövirta

Muut vektorien väliset toiminnot

Vektorien summan ja vähentämisen lisäksi erittäin tärkeiden vektoreiden välillä on kolme muuta toimintaa, koska ne aiheuttavat uusia erittäin tärkeitä fyysisiä suuruuksia:

-Vektorien skalaarin tuote.

-Skalaarituote tai pistetuote vektorien välillä

-Ja risti- tai vektorituote kahden vektorin välillä.

Vektorien skalaarin tuote

Harkitse Newtonin toista lakia, jossa todetaan tämä joukko F ja kiihtyvyys -lla Ne ovat verrannollisia. Suhteellisuusvakio on massa m objektista, siksi:

F = m.-lla

Taikina on skalaari; Vahvuus ja kiihtyvyys puolestaan ​​ovat vektoreita. Koska voima saadaan kertomalla massa kiihtyvyydellä, se on seurausta skalaarin tuotteesta vektorilla.

Voi palvella sinua: Esimerkkejä teoreettisista kehyksistä

Tämäntyyppinen tuote johtaa aina vektoriin. Tässä toinen esimerkki: liikkeen määrä. Olla P Liikkeen vektorimääräinen määrä, v Nopeusvektori ja kuten aina, m on massa:

P = m.v

Skalaarituote tai pistetuote vektorien välillä

Olemme sijoittaneet mekaanista työtä suuruusluetteloon, jotka eivät ole vektoreita. Fysiikan työ on kuitenkin seurausta skalaarituotteesta, sisäisestä tuotteesta tai pistetuotteesta kutsuttujen vektorien välisestä toiminnasta.

Olla vektoria v ja tai, Kohta tai kiipeilytuote määritetään niiden välillä:

v∙tai = |vJa ∙ |tai Ja.cos θ

On θ niiden välinen kulma. Esitetystä yhtälöstä päätellään heti, että pistetuotteen tulos on skalaari ja myös jos molemmat vektorit ovat kohtisuorassa, niiden skalaarituote on 0.

Takaisin mekaaniseen työhön W -, Tämä on skalaarituote vahvuusvektorin välillä F ja vektorin siirtymä ℓ.

W = F∙ℓ                  

Kun vektoreita on saatavana niiden komponenttien suhteen, pistemerkki on myös hyvin helppo laskea. Joo v = x, v_ja, v_{z -z} - ja tai = x, tai_ja, tai_{z -z} -, Pistetuote näiden kahden välillä on:

v∙tai = v_x tai_x + v_ja tai_ja + v_{z -z} tai_{z -z}

Vektoreiden välinen pistetuote on siksi kommutatiivinen,:

v∙tai = tai∙v

Ristituotteen tai vektorituote vektorien välillä

Joo v ja u ovat kaksi esimerkkivektoriamme, vektorituote määritetään seuraavasti:

v x tai = W -

Tästä seuraa heti, että ristituote johtaa vektoriin, jonka moduuli on määritelty:

Jav x U | = | V | . | u |. synti θ

Missä θ Se on vektorien välinen kulma.

Ristituote ei siis ole kommutatiivinen v x u ≠ u x v. Itse asiassa v x U = - (u x V).

Jos kaksi esimerkkivektoria ilmaistaan ​​yksikkövektoreina, vektorituotteen laskemista helpotetaan:

v = v_x Yllyttää + v_ja J - + v_{z -z} k -k -

tai = u_x Yllyttää + tai_ja J - + tai_{z -z} k -k -

Ristituotteet yksikkövektoreiden välillä

Ristituote identtisten yksikkövektoreiden välillä on nolla, koska niiden välinen kulma on 0º. Mutta eri yksikkövektoreiden keskuudessa niiden välinen kulma on 90º ja synnit 90º = 1.

Seuraava järjestelmä auttaa löytämään nämä tuotteet. Nuolen suuntaan on positiivinen järkevä ja vastakkaiseen suuntaan:

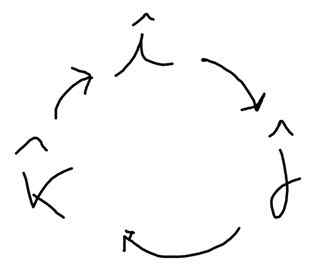
Yllyttää x J - = K, J x k -k - = Yo; k -k - x Yllyttää = J; J - x i = -k; k -k - x J - = -Yo; Yllyttää x k -k - = -J -

Jakautuvan ominaisuuden soveltaminen, joka pysyy voimassa tuotteille vektorien keskuudessa sekä yksikkövektoreiden ominaisuudet, sinulla on:

v x tai = (v_x Yllyttää + v_ja J - + v_{z -z} k -k -) X (u_x Yllyttää + tai_ja J - + tai_{z -z} k -k -) =  

= (v_jatai_{z -z} - v_{z -z}tai_ja -AYllyttää + (V_{z -z}tai_x - v_xtai_{z -z} -AJ - + (V_xtai_ja - v_jatai_x -Ak -k -

Ratkaisut

- Harjoitus 1

Ottaen huomioon vektorit:

v = -5 Yllyttää + 4J - + 1 k -k -

tai = 2 Yllyttää -3 J - + 7k -k -

Mikä pitäisi olla vektori W - niin summa v + tai + W - tulokset 6 Yllyttää +8 J - -10k -k -?

Ratkaisu

-5 Yllyttää + 4J - + 1 k -k -

2 Yllyttää -3 J - + 7k -k -

 W -_x Yllyttää + W -_ja J - + W -_{z -z} k -k -  +

--

6Yllyttää + 8 J - -10 k -k -

Siksi on täytettävä, että:

-5 +2 + W_x = 6 → W_x = 9

4-3 + W_ja = 8 → W_ja = 7

1 + 7 + W_{z -z} = -10 → W_{z -z} = -18

Vastaus on: W - = 9 Yllyttää +7 J - - 18k -k -

- Harjoitus 2

Mikä on vektorien välinen kulma v ja tai harjoituksen 1?

Ratkaisu

Käytämme skalaarituotetta. Meillä on:

cos θ = v∙tai / |vJa ∙ |taiJa

v∙tai= -10 -12+7 = -15

Jav| = √ (-5)² +4² +1²= √42 = 6.48

Jatai| = √2² +(-3)² +7²= √62 = 7.87

Näiden arvojen korvaaminen:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.Ensimmäinen

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
3. Rex, a. 2011. Fysiikan perusteet. Pearson.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Serway, R., Jewett, J. 2008. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.