Vektorijohtaja Linjan yhtälö, ratkaisut harjoitukset
- 2810
- 425
- Dr. Travis Reichert
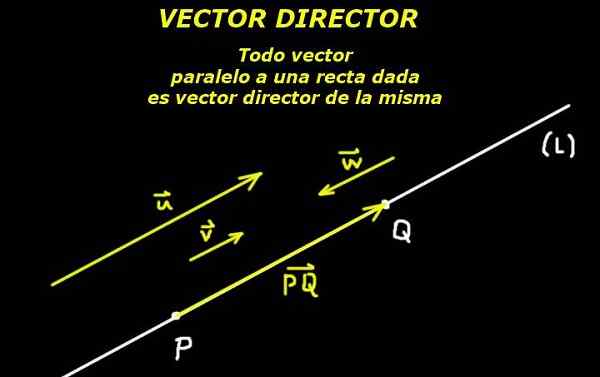
Se ymmärretään Johtajavektori Se, joka määrittelee linjan suunnan joko tasossa tai avaruudessa. Siksi linjan suuntaista vektoria voidaan pitää saman johtajana.
Tämä on mahdollista euklidisen geometrian aksiooman ansiosta, jonka mukaan kaksi pistettä määrittelevät viivan. Sitten nämä kaksi pistettä muodostava suuntautunut segmentti määrittelee myös kyseisen linjan vektorijohtajan.
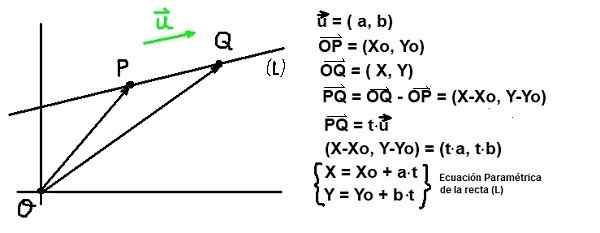
Kuvio 1. Linjan vektorijohtaja. (Oma yksityiskohta) Annetun pisteen P linjalle (L) ja annetaan ohjaajavektori tai Tuosta linjasta linja on täysin määritetty.
[TOC]
Linja- ja johtajayhtälö
Kuva 2. Linja- ja johtajayhtälö. (Oma yksityiskohta) Annetun pisteen P koordinaatit K: (XO, minä) ja vektori tai Linjan johtaja (L), Kaikki kohta Q - koordinaatit K: (x, y) Täytyy täyttää vektori Pq olla yhdensuuntainen u. Tämä viimeinen ehto on taattu, jos Pq Se on verrannollinen tai-
Pq = t⋅tai
Edellisessä ilmaisussa t Se on parametri, joka kuuluu reaalilukuihin.
Jos Cartesian komponentit Pq ja tai Edellinen yhtälö on kirjoitettu seuraavasti:
(X-xo, y-yo) = t⋅ (a, b)
Jos vektorien tasa -arvon komponentit ovat yhtä suuret kuin seuraavat yhtälöparit:
X - xo = a⋅t ja Ja - minä = b⋅t
Viivan parametrinen yhtälö
Koordinaatit X ja JA linjalle kuuluva piste (L) Se käy läpi koordinaattipisteen (Xo, minä) Ja se on yhdensuuntainen Johtajavektori tai= (a, b) Ne määritetään määrittämällä todelliset arvot muuttujan parametrille t:
X = xo + a⋅t; Y = minä + b⋅t
Esimerkki 1
Linjan parametrisen yhtälön merkityksen havainnollistamiseksi otamme ohjaajavektorina
Voi palvella sinua: aaltoileva optiikkatai = (a, b) = (2, -1)
ja linjan tunnetun pisteenä pisteenä
P = (xo, me) = (1, 5).
Linjan parametrinen yhtälö on:
X = 1 + 2⋅t; Y = 5 - 1⋅T; ∞
Tämän yhtälön merkityksen havainnollistamiseksi Kuva 3 osoittaa, missä parametri T muuttaa arvoa ja pistettä Q - koordinaatit (X, y) Ottaa linjalle erilaisia asentoja.
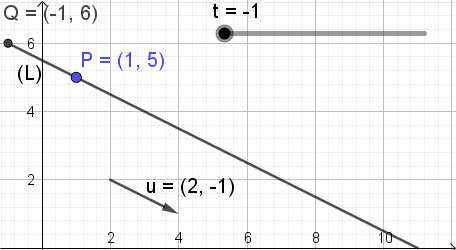Kuva 3. Pq = t u. (Oma yksityiskohta) Linja vektorimuodossa
Annetaan linjan P ja sen johtaja tai linjan yhtälö voidaan kirjoittaa vektorimuodossa:
O q = Oppi + λ⋅tai
Edellisessä yhtälössä, joka on mikä tahansa kohta, mutta kuuluu linjalle ja λ Todellinen luku.
Linjan vektoriyhtälöä voidaan soveltaa mihin tahansa määrään mittoja, jopa hyper-eret voidaan määritellä.
Ohjaajavektorin kolmiulotteisessa tapauksessa tai= (a, b, c) Ja kohta P = (xo, minä, Zo), Yleisen pisteen koordinaatit Q = (x, y, z) Linjalle kuuluminen on:
(X ja z) = (Xo, i, zo) + λ⋅ (a, b, c)
Esimerkki 2
Harkitse jälleen linjaa, joka on ohjaajana
tai = (a, b) = (2, -1)
ja linjan tunnetun pisteenä pisteenä
P = (xo, me) = (1, 5).
Tämän viivan vektoriyhtälö on:
(X, y) = (1, 5) + λ⋅ (2, -1)
Jatkuva linjan ja ohjaajavektorin muoto
Alkaen parametrisesta muodosta, puhdistamalla ja sovittamalla parametri λ:
(X-xo)/a = (y-yo)/b = (z-zo)/c
Tämä on viivayhtälön symmetrinen muoto. minusta tuntuu että -lla, b - ja c Ne ovat ohjaajavektorin komponentteja.
Esimerkki 3
Harkitse linjaa, joka on ohjaajana
tai = (a, b) = (2, -1)
ja linjan tunnetun pisteenä pisteenä
Voi palvella sinua: mikä on sähkö? (Kokeella)P = (xo, me) = (1, 5). Löydä sen symmetrinen muoto.
Symmetrinen tai jatkuva muoto on linja on:
(X - 1)/2 = (y - 5)/( - 1)
Viivayhtälön yleinen muoto
Sitä kutsutaan XY -tasossa olevan viivan yleiseksi muotoksi yhtälöön, joka seuraavalla rakenteella on:
A⋅x + b⋅y = c
Symmetrisen muodon ilmaisu voidaan kirjoittaa uudelleen siten, että sillä on yleinen muoto:
B⋅x - a⋅y = b⋅xo - a⋅o
Verrattuna linjan yleiseen muotoon on edelleen:
A = b, b = -a ja c = B⋅xo - a⋅o
Esimerkki 3
Löydä linjan yleinen muoto, jonka ohjaaja on U = (2, -1)
Ja mikä tapahtuu piste P = (1, 5).
Yleisen lomakkeen löytämiseksi voimme käyttää annettuja kaavoja, mutta vaihtoehtoinen polku valitaan.
Aloitamme etsimällä U -vektorin kaksoisvektoria, joka on määritelty vektoriksi, joka saadaan vaihtamalla U: n komponentit ja kertomalla -1 toisella:
W -= (-1, -2)
Kaksoisvektori W - Vastaa kiertoa 90 °: ssa ohjaajan aikataulussa v.
Kerrota kiipeämme W - kanssa (X, y) ja kanssa (Xo, minä) Ja me sovitamme:
(-1, -2) • (x, y) = (-1, -2) • (1, 5)
-X -2Y = -1 -2⋅5 = -11
Lopuksi jäljellä:
X + 2y = 11
Viivayhtälön vakiomuoto
Sitä kutsutaan XY -tasossa olevan viivan vakiomuotona, jolla on seuraava rakenne:
Y = m⋅x + d
missä m edustaa kaltevuutta ja D -sieppausta akselin kanssa ja.
Ottaen huomioon ohjaaja u = (a, b) vektori, kaltevuus m on b/a.
Ja D saadaan korvaamalla X ja Y tunnetulla pisteellä XO, minä:
I = (b/a) xo + d.
Lyhyesti sanottuna, m = b/a y d = me -(b/a) xo
Huomaa, että kaltevuus m on komponentin välinen osuus ja ohjaaja ja komponentti x samasta.
Voi palvella sinua: Kiertotasapaino: Kaavat ja yhtälöt, esimerkit, harjoituksetEsimerkki 4
Löydä linjan vakiomuoto, jonka ohjaaja on U = (2, -1)
Ja mikä tapahtuu piste P = (1, 5).
M = -½ ja d = 5 -( -½) 1 = 11/2
Y = (-1/2) x + 11/2
Ratkaisut
-Harjoitus 1
Löydä viivan (L) vektorijohtaja, joka on tason (π): x - y + z = 3 ja tason (ω) leikkauspiste: 2x + y = 1.
Kirjoita sitten linjan rivin jatkuva muoto (l).
Ratkaisu
Tasoyhtälöstä (ω) välys y: y = 1 -2x
Sitten korvaamme tasoyhtälössä (π):
X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x
Sitten parametroimme x, valitsemme parametroinnin x = λ
Tämä tarkoittaa, että viivalla on vektoriyhtälö:
(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)
Se voidaan kirjoittaa uudelleen:
(X, y, z) = (0, 1, 4) + λ (1, -2, -3)
Mikä on selvää, että vektori tai = (1, -2, -3) on suora hallintavektori (l).
Linjan jatkuva muoto (l) on:
(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)
-Harjoitus 2
Kun otetaan huomioon 5x -taso + -lla Y + 4z = 5
ja linja, jonka yhtälö on x/1 = (y-2)/3 = (z -2)/(-2)
Määritä arvo -lla niin, että taso ja viiva ovat yhdensuuntaiset.
Ratkaisu 2
Vektori n = (5, A, 4) on normaali vektori tasolle.
Vektori tai = (1, 3, -2) on suora johtaja.
Jos viiva on yhdensuuntainen tason kanssa, niin niin n • v = 0.
(5, -lla, 4)Olla(1, 3, -2) = 5 +3-lla -8 = 0 ⇒ -lla= 1.
Viitteet
- Fleming, w., & Varberg, D. JA. (1989). Prealculus -matematiikka. Prentice Hall Ptr.
- Kolman, b. (2006). Lineaarialgebra. Pearson -koulutus.
- Uskollinen, j. M., & Viloria, N. G. (2005). Litteä analyyttinen geometria. Mérida - Venezuela: Venezuelan toimituksellinen C. -Lla.
- Navarro, Rocio. Vektorit. Toipunut: Kirjat.Google.yhteistyö.mennä.
- Pérez, c. D -d. (2006). Prequalculus. Pearson -koulutus.
- Prenowitz, w. 2012. Geometrian peruskäsitteet. Rowman & Littlefield.
- Sullivan, M. (1997). Prequalculus. Pearson -koulutus.