Normaali laskenta ja esimerkkivektori

Hän Normaali vektori Se määrittelee suunnan kohtisuorassa tarkasteltavana olevaan geometriseen kokonaisuuteen nähden, joka voi olla käyrä, esimerkiksi taso tai pinta,.

Se on erittäin hyödyllinen käsite liikkuvan hiukkasen tai jonkin pinnan sijainnissa avaruudessa. Seuraavassa kaaviossa on mahdollista nähdä, kuinka normaali vektori on mielivaltainen käyrä C-

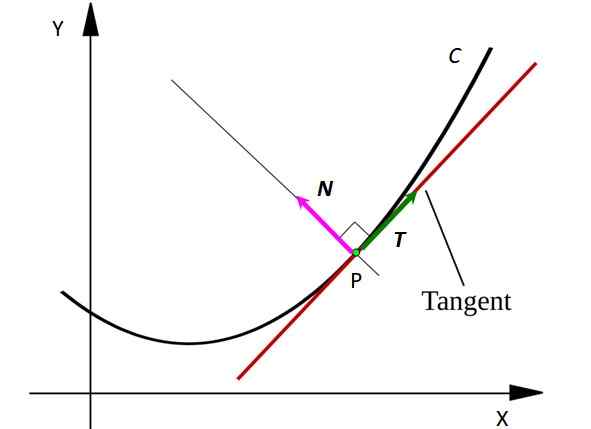
Kuvio 1. C -käyrä normaalin vektorin kanssa käyrään pisteessä P. Lähde: SVJO [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Harkitse kohtaa käyrässä C. Kohta voi edustaa liikkuvaa hiukkasia, joka liikkuu C -muotoisen tien jälkeen. Viiva tangentti käyrään pisteessä P näyttää olevan vedetty punaiseksi.

Huomaa, että vektori T Se on tangentti C: lle jokaisessa pisteessä, kun taas vektori N on kohtisuorassa T ja viittaa kuvitteellisen ympärysmiilleen, jonka kaari on c -segmentti. Vektorit on merkitty lihavoituna kirjaimella painettuna tekstissä, jotta ne voidaan erottaa muista ei -vektorin suuruuksista.

Vektori T Se osoittaa aina, missä hiukkas liikkuu, siksi se osoittaa saman nopeuden. Sen sijaan vektori N Aina osoita siihen suuntaan, johon hiukkanen kääntyy, tällä tavalla se osoittaa C -käyrän koveruuden.

[TOC]

Kuinka saada normaali vektori tasolle?

Normaali vektori ei välttämättä ole yksikkövektori, ts. Vektori, jonka moduuli on 1, mutta jos niin, sitä kutsutaan Normaali yksikkövektori.

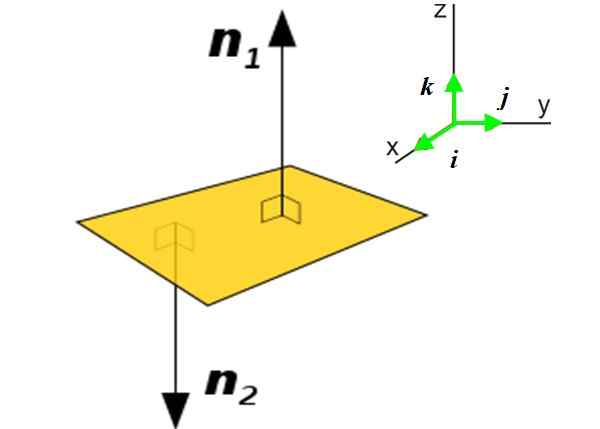Kuva 2. Vasemmalla P -taso ja kaksi normaalia vektoria mainitulle tasolle. Oikealla yksikkövektorit kolmessa suunnassa, jotka määrittävät tilan. Lähde: Wikimedia Commons. Katso kirjoittajan sivu [julkinen verkkotunnus]

Lukuisissa sovelluksissa on tarpeen tuntea normaali vektori tasolle käyrän sijasta. Tämä vektori ilmoittaa mainitun tason suunnan avaruudessa. Harkitse esimerkiksi tasoa P (keltainen) kuva:

Se voi palvella sinua: Gemine: Origins, ominaisuudet ja miten niitä tarkkailla

Tasossa on kaksi normaalia vektoria: n₁ ja n₂. Yhden tai toisen käyttö riippuu tilanteesta, jossa mainittu taso löytyy. Normaalin vektorin saaminen tasolle on hyvin yksinkertaista, jos sen yhtälö tunnetaan:

Ax + + cz + d = 0, kanssa -lla, b -, c ja d -d todelliset numerot.

No, normaali tasovektori antaa:

N = a Yllyttää + b - J - + c k -k -

Tässä vektori N ilmaistaan ​​yksikkövektoreina ja kohtisuorassa toisiinsa nähden Yllyttää, J - ja k -k -, Ohjattu koko kolmeen suuntaan, jotka määrittävät tilan X ja z, Katso kuva 2 oikeassa.

Normaali vektori vektorituotteesta

Hyvin yksinkertainen menettely normaalin vektorin löytämiseksi käyttää vektorituotteen ominaisuuksia kahden vektorin välillä.

Kuten tiedetään, kolme eri pistettä ja ei kolineaalisia keskenään, määritä P -taso. Nyt on mahdollista saada kaksi vektoria tai ja v jotka kuuluvat mainittuun lentokoneeseen, jolla on nämä kolme pistettä.

Kun vektorit ovat, Vektorituote tai x v Se on operaatio, jonka tulos on vektori, jonka ominaisuus on kohtisuorassa määritettyyn tasoon nähden tai ja v.

Tunnet tämän vektorin, se on merkitty nimellä N, Ja siitä on mahdollista määrittää tason yhtälö edellisessä osassa ilmoitetun yhtälön ansiosta:

N = tai x v

Seuraava kuva kuvaa kuvattua menettelyä:

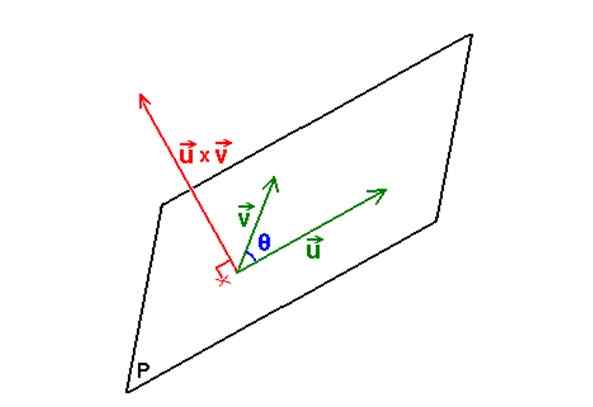Kuva 3. Kahdella vektorilla ja niiden vektorilla tai ristituotteella määritetään kaksi vektoria sisältävän tason yhtälö. Lähde: Wikimedia Commons. Ei konetta luettavissa olevaa kirjailijaa. M.Romero Schmidtke oletti (tekijänoikeusvaatimusten perusteella). [Julkinen verkkotunnus]

Esimerkki

Löydä pisteiden A (2,1,3) määritetty tasayhtälö (2,1,3); B (0,1,1); C (4,2,1).

Voi palvella sinua: Jatkuvuusyhtälö

Ratkaisu

Tämä harjoitus kuvaa yllä kuvattua menettelyä. 3 pisteellä yksi niistä valitaan kahden vektorin yleiseksi alkuperäksi, jotka kuuluvat näiden pisteiden määrittelemään tasoon. Esimerkiksi piste A on asetettu alkuperäksi ja vektorit on rakennettu Ab ja Ac.

Vektori Ab Se on vektori, jonka alkuperä on kohta A ja jonka loppu on kohta B. Vektorin koordinaatit Ab A: n koordinaatit: A:

Ab = (0-2) Yllyttää + (1-1) J - + (1-3) k -k - = -2Yllyttää + 0 -J - -2 k -k -

Jatka samalla tavalla vektorin löytämiseksi Ac-

Ac = (4-2) Yllyttää + (2-1) J - + (1-3) k -k - = 2Yllyttää + J - -2 k -k -

Vektorituotteen laskenta AB X AC

Vektorituotteen löytämiseksi kahden vektorin välillä on useita menettelytapoja. Tässä esimerkissä käytetään muistomenetelmää, joka käyttää seuraavaa kuvaa vektorituotteiden löytämiseen yksikkövektorien joukosta Yllyttää, J - ja K:

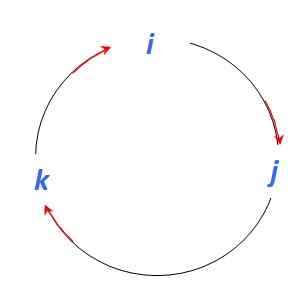Kuva 4. Graafinen vektorituotteen määrittämiseksi yksikkövektorien välillä. Lähde: Itse tehty.

Aluksi on hyvä muistaa, että vektorituotteet rinnakkaisvektoreiden välillä ovat tyhjiä, siksi:

Yllyttää x Yllyttää = 0; J - x J - = 0; k -k - x k -k - = 0

Ja koska vektorituote on toinen vektori, joka on kohtisuorassa osallistuville vektoreille, siirtyen punaisen nuolen suuntaan:

Yllyttää x J - = k -k - ; J - x k -k - = Yllyttää; k -k - x Yllyttää = J -

Jos joudut liikkumaan nuolen vastaisesti, lisätään merkki (-):

J - x Yllyttää = - k -k -; k -k - x J - = -Yllyttää; Yllyttää x k -k - = -J -

Kaiken kaikkiaan on mahdollista tehdä 9 vektorituotetta yksikkövektoreiden kanssa Yllyttää, J - ja k -k -, joista 3 on mitätön.

Ab x Ac = (-2Yllyttää + 0 -J - -2 k -k -) X (2Yllyttää + J - -2 k -k -) = -4 (Yllyttää x Yllyttää) -2 (Yllyttää x J -) +4 (Yllyttää x k -k -) +0 (J - x Yllyttää) + 0 (J - x J -) - 0 (J - x k -k -) - 4 (k -k - x Yllyttää) -2 (k -k - x J -) + 4 (k -k - x k -k -) = -2k -k --4J --4J -+2Yllyttää = 2Yllyttää -8J --2k -k -

Tasoyhtälö

Vektori N on määritetty aikaisemmin lasketulla vektorituotteella:

Voi palvella sinua: Pendulaarinen liike

N = 2Yllyttää -8J --2k -k -

Siksi a = 2, b = -8, c = -2, haetaan suunnitelma:

Ax + + cz + d = 0 → 2x-8y-2z + d = 0

Arvo d -d. Tämä on helppoa, jos minkä tahansa pisteiden A, B tai C arvot korvataan tasoyhtälössä. Esimerkiksi C: n valitseminen:

x = 4; y = 2; Z = 1

On jäljellä:

2.4 - 8.2 - 2.1 + d = 0

-10 + d = 0

D = 10

Lyhyesti sanottuna, haluttu lentokone on:

2x-8y-2z +10 = 0

Utelias lukija voi kysyä, olisiko sama tulos saatu, jos tekemisen sijaan Ab x Ac Se olisi valittu Ac x Ab. Vastaus on kyllä, näiden kolmen pisteen määrittämä taso on ainutlaatuinen ja siinä on kaksi normaalia vektoria, kuten kuvassa 2 esitetään.

Valittujen pisteen osalta vektorien alkuperänä ei myöskään ole haittaa valinnassa mitään muuta kahdesta.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB). 31-62.
2. Normaalin löytäminen tasolle. Haettu: Web.mehu.UTEXAS.Edu.
3. Larson, r. (1986). Laskenta ja analyyttinen geometria. MC Graw Hill. 616 - 647.
4. Linjat ja suunnitelmat R 3: ssa. Toipunut: matematiikka.Harvard.Edu.
5. Normaali vektori. Toipunut Mathworldista.Susi.com.