Vektorit avaruudessa Kuinka kuvaaja, sovelluksia, harjoituksia

Eräs vektori avaruudessa Sitä edustaa koordinaattijärjestelmä, jonka on annettu x, ja ja z -z. Melkein aina lentokone Xy Se on vaakasuoran pinnan ja akselin taso z -z edustaa korkeutta (tai syvyyttä).

Kartesian koordinaattiakselit, jotka on esitetty kuvassa 1, jaa tila 8 alueelle, joita kutsutaan Oktaverit, analoginen akselien kanssa x - ja Jaa taso 4 kvadranttiin. Sitten meillä on yksi oktantti, toinen ocanto ja niin edelleen.

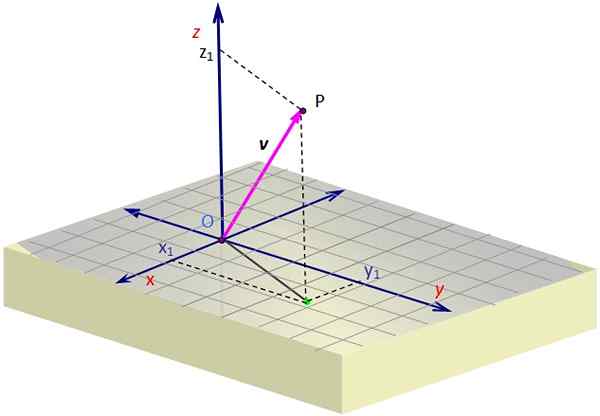
Kuvio 1. Vektori avaruudessa. Lähde: Itse tehty.

Kuvio 1 sisältää vektorin esityksen v avaruudessa. Jonkin verran näkökulmaa tarvitaan kolmen ulottuvuuden illuusion luomiseksi näytön tasossa, joka saavutetaan piirtämällä vinot näkymä.

3D -vektorin piirtämiseksi sinun on autettava katkoviivoja, jotka määrittävät ruudukon projektion tai "varjon" koordinaatit v Pinnan yli x-ja. Tämä projektio alkaa O: ssa ja päättyy vihreään kohtaan.

Kun siellä sinun on jatkettava pystysuoran korkeutta (tai syvyyttä), joka on tarpeen arvon mukaisesti z -z, Kunnes pääset p. Vektori on piirretty O: sta ja päättyy p: hen, joka on esimerkissä ensimmäisessä ocantissa.

[TOC]

Sovellukset

Avaruuden vektoreita käytetään laajasti mekaniikassa ja muissa fysiikan ja tekniikan haaroissa, koska meitä ympäröivät rakenteet vaativat geometriaa kolmessa ulottuvuudessa.

Avaruuden sijaintivektoreita käytetään objektien sijoittamiseen suhteessa viitepisteeseen, jota kutsutaan alkuperä JOMPIKUMPI. Siksi ne ovat myös välttämättömiä työkaluja navigoinnissa, mutta se ei ole kaikki.

Voi palvella sinua: Sähkömagneettiset aallot: Maxwell -teoria, tyypit, ominaisuudet

Rakenteisiin, kuten pultteihin, tukeviin, kaapeliin, tukkeihin ja muihin rakenteisiin vaikuttavat voimat ovat vektori luonnetta ja suuntautuvat avaruuteen. Sen vaikutuksen tietämiseksi on tarpeen tietää osoitteesi (ja myös sovelluspisteen).

Ja usein voiman suunta tunnetaan kahdella pisteellä avaruudessa, jotka kuuluvat sen toimintalinjaan. Tällä tavalla voima on:

F = F tai

Missä f on voiman voimakkuus tai moduuli ja tai Se on yksikkövektori (moduuli 1), joka on suunnattu F. 

3D -vektorimerkki ja esitykset

Ennen joidenkin esimerkkien ratkaisemista 3D -vektorien merkintä tarkistetaan lyhyesti.

Kuvion 1 esimerkissä Vector V, jonka alkuperäpiste on samaan aikaan kuin alkuperää tai ja jonka päättyminen on piste P, on koordinaatit x ja z -z positiivinen, samalla kun se koordinoi ja Se on negatiivinen. Nämä koordinaatit ovat: x₁, ja₁, z -z₁, jotka ovat juuri p: n koordinaatit.

Joten jos meillä on vektori, joka on kytketty alkuperään, eli, jonka lähtökohta on samaan aikaan O: n kanssa, on erittäin helppo osoittaa sen koordinaatit, jotka ovat äärimmäisen tai p: n koordinaatit. Pisteen ja vektorin erottamiseksi käytämme viimeisimpiä rohkeita kirjaimia ja suluissa, kuten tämä:

v = < x₁, ja₁, z -z₁ -

Vaikka piste P on merkitty suluilla:

P = (x₁, ja₁, z -z₁-A

Toinen esitys käyttää yksikkövektoreita Yllyttää, J - ja k -k - jotka määrittelevät akselien kolme tilaa x, ja ja z -z vastaavasti.

Nämä vektorit ovat kohtisuorassa toisiinsa ja muodostavat a Ortonormal -pohja (Katso kuva 2). Tämä tarkoittaa, että 3D -vektori voidaan kirjoittaa niistä seuraavasti:

Voi palvella sinua: aaltoileva liike: ominaisuudet, aaltotyypit, esimerkit

v = v_x Yllyttää + v_ja J - + v_{z -z} k -k -

Vektorin kulmat ja kosenosin johtajat

Kuvio 2 näyttää myös ohjaajat γ -kulmat₁, γ₂ ja γ₃ kuin vektori v vastaavasti akselien kanssa x, ja ja z -z. Tietäen nämä näkökulmat ja vektorin suuruus, tämä on täysin määritetty. Lisäksi johtajien kosinit täyttävät seuraavan suhteen:

(cos γ₁-A² + (cos γ₂-A² + (cos γ₃-A² = 1

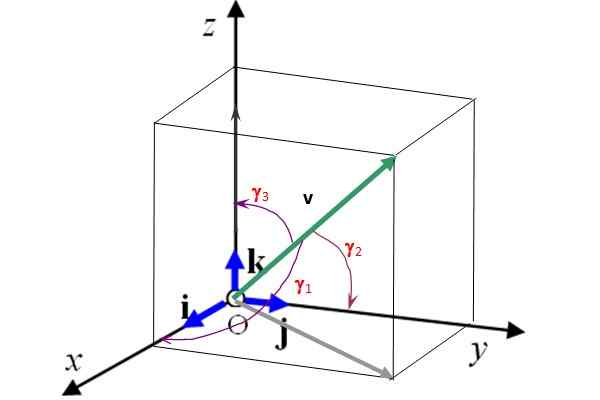Kuva 2. Yhtenäiset vektorit I, J ja K määrittävät 3 avaruuden etusijalle. Lähde: Itse tehty.

Ratkaisut

-Harjoitus 1

Kuviossa 2 y -kulmat₁, γ₂ ja γ₃ kuin vektori v moduuli 50 -muoto koordinaattiakseleilla on vastaavasti: 75.0º, 60.0º ja 34.Kolmas. Etsi tämän vektorin Cartesian -komponentit ja edusta sitä yksikkövektoreiden suhteen Yllyttää, J - ja k -k -.

Ratkaisu

Vektorin projektio v akselilla x on v_x = 50 . Cos 75º = 12.941. Samoin projektio v akselilla ja on v_ja = 50 cos 60 º = 25 ja lopuksi akselilla z -z on v_{z -z} = 50. cos 34.3. = 41.3. Nyt v voidaan ilmaista seuraavasti:

v = 12.9 Yllyttää + 25.0 - J - + 41.3 k -k -

-Harjoitus 2 

Löydä jännitteitä jokaisesta kaapelista, jotka pitävät luvun kauhaa, joka on tasapainossa, jos tämän paino on 30 N.

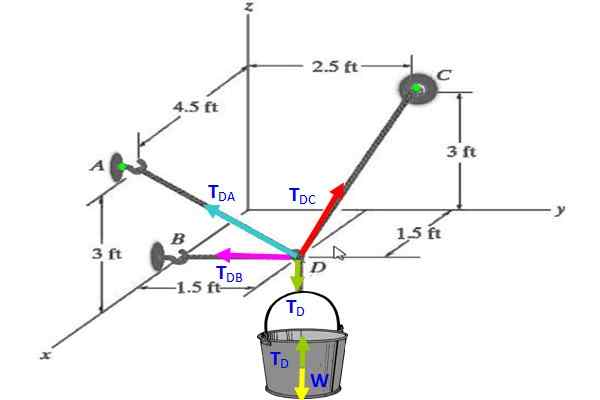Kuva 3. Jännitteet Kaavio harjoitukselle 2.

Ratkaisu

Kauhassa vapaa kehon kaavio osoittaa sen T_{D -d} (vihreä) kompensoi painoa W - (keltainen), siksi t_{D -d} = W = 30 N.

Solmussa, vektori T_{D -d}  Se on suunnattu pystysuoraan alas, sitten:

T_{D -d} = 30 (-k -k -) N.

Jäljellä olevien jännitteiden määrittämiseksi sinun on noudatettava seuraavia vaiheita:

Vaihe 1: Etsi kaikkien pisteiden koordinaatit

A = (4.5; 0; 3) (A on seinätasolla X-Z-A

B = (1.5; 0; 0) (B on x -akselilla)

Voi palvella sinua: osoite (fyysinen)

C = (0, 2.5, 3) (C on seinätasolla ja z-A

D = (1.5; 1.5; 0) (D on vaakasuorassa tasossa  x-ja-A

Vaihe 2: Etsi vektorit kumpaankin suuntaan vähentämällä lopun ja alun koordinaatit

Antaa =

DC =

Db =

Vaihe 3: Laske moduulit ja yksikkövektorit

Yksikkövektori saadaan lausekkeella: tai = r - / r, r - (lihavoitu) on vektori ja R (ilman lihavoitu) mainitun vektorin moduuli.

Da = (3² + (-1.5)² + 3²-A^½ = 4.5; DC = ((-1.5) ² + 1² + 3²-A^½ = 3.5

tai_Antaa = 4.5 =

tai_DC = 3.5 =

tai_Db =

tai_{D -d} =

Vaihe 4: Ilmaise kaikki jännitteet vektoreina

T_Antaa = T_Antaa tai_Antaa = T_Antaa

T_DC = T_DC tai_{DC =}  T_DC

T_Db = T_Db tai_Db = T_Db

 T_{D -d} = 30

Vaihe 5: Käytä staattista tasapainoolosuhteita ja ratkaise yhtälöjärjestelmä

Lopuksi, staattista tasapainoolosuhdetta sovelletaan kauhaan, niin että kaikkien solmun voimien vektorisumma on mitätön:

T_Antaa + T_DC + T_Db + T_{D -d} = 0

Koska jännitteet ovat avaruudessa, se johtaa kolmeen yhtälöjärjestelmään jokaiselle komponentille (x, ja ja z -z) jännitteet.

0 -.67 t_Antaa -0 -.43 t_DC + 0 T_Db = 0

-0 -.33 t_Antaa + 0 -.29 t_DC - T_Db = 0

0 -.67 t_Antaa + 0 -.86 t_DC +0 T_Db - 30 = 0

Ratkaisu on: t_Antaa = 14.9 n; T_Antaa = 23.3 n; T_Db = 1.82 n

Viitteet

1. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley. 38-52.
2. Figueroa, D. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka.31-68.
3. Fyysinen. Moduuli 8: Vektorit. Toipunut: FRTL.Utn.Edu.AR
4. Hibbeler, R. 2006. Insinöörien mekaniikka. Staattinen. 6. painos. Mannertoimitusyhtiö. 15-53.
5. Lisäyslaskinvektori. Toipunut: 1728.org