Balancer -vektorilaskelma, esimerkit, harjoitukset

Hän tasapainotusvektori Se on se, joka ristiriidassa tuloksena olevan vektorin kanssa ja siksi se pystyy tasapainottamaan järjestelmän, koska sillä on sama ja sama suunta, mutta vastoin tätä.

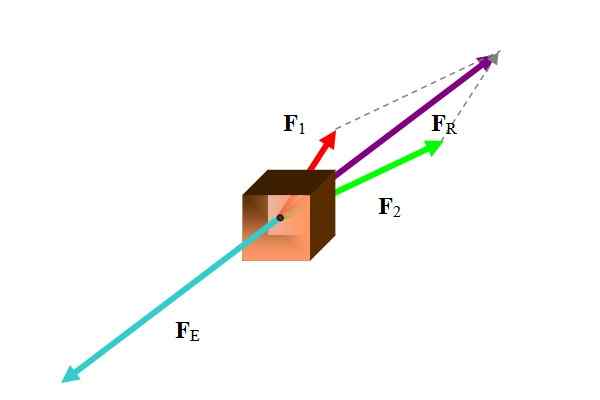
Usein tasapainottava vektori viittaa voimavektoriin. Tasapainotusvoiman laskemiseksi tuloksena oleva voima on ensin, kuten seuraavassa kuvassa esitetään:

Kuvio 1. Kehoon kaksi voimaa, jonka tuloksena on tasapainotettu turkoosi värillä. Lähde: Itse tehty.

Tämän tehtävän suorittamiseksi on olemassa useita menetelmiä käsillä olevien tietojen mukaan. Koska voimat ovat vektoreita, tuloksena on osallistuvien joukkojen vektorisumma:

F_{R -} = F₁ + F₂ + F₃ +  .. .

Käytettävien menetelmien joukossa ovat graafiset menetelmät, kuten monikulmaiset, rinnakkaisogrammi ja analyyttiset menetelmät, kuten voimien hajoaminen niiden karteesikomponenteissa. Esimerkissä kuvio käytettiin rinnakkaisogrammimenetelmää.

Kun tuloksena oleva voima on löydetty, tasapainotusvoima on juuri päinvastainen vektori.

Joo F_JA Se on tasapainottava voima, niin täytetään F_JA Tietyssä vaiheessa se takaa järjestelmän käännöksen tasapainon. Jos se on yksi hiukkas, se ei liiku (tai ehkä se tekee sen jatkuvalla nopeudella), mutta jos se on laajennettu esine, sillä on silti mahdollisuus kääntyä:

F_{R -} + F_JA = 0 -

[TOC]

Esimerkit

Tasapainotusvoimat ovat läsnä kaikilla puolilla. Meitä itse tasapainottaa voima, jonka tuoli käyttää painoa kompensoimaan. Lepoista löytyvät esineet: Kirjat, huonekalut, kattovalaisimet ja suuri määrä mekanismeja tasapainottavat jatkuvasti voimat.

Voi palvella sinua: joustavat iskut: ulottuvuudessa ja esimerkeissä

Esimerkiksi lepokirja pöydällä tasapainottaa normaali voima, jota se käyttää kirjaan, estäen sen putoamisen. Sama pätee ketjuun tai kaapeliin, joka pitää huoneen katosta roikkuvan lampun. Kaapelit, jotka pitävät kuormaa.

Nesteessä jotkut esineet kykenevät kellumaan ja pysymään levossa, koska niiden painoa tasapainottaa nesteen kohdistama nouseva voima, nimeltään työntää.

Erilaisia ​​mekanismeja on tasapainotettava tasapainotusvoimavektorin, kuten tankojen, palkkien ja pylväiden, tunteminen.

Tasapainoa käytettäessä on välttämätöntä tasapainottaa esineen paino ekvivalenttilla voimalla, joko painon lisääminen tai jouset.

Joukkojen taulukko

Voimataulukkoa käytetään laboratoriossa tasapainoisen voiman määrittämiseksi. Se koostuu ympyräalustasta, josta sinulla on ylempi näkymä kuvassa, ja siinä on kuljettaja kulmien mittaamiseksi.

Taulukon reunoilla on hihnapyöriä, joiden läpi jouset, jotka pitävät painoja ja jotka lähentyvät keskuksessa olevaan kehään.

Esimerkiksi kaksi painoa ripustetaan. Näiden painojen jousilla syntyvät jännitteet piirretään punaisella ja sinisellä kuvassa 2. Kolmas painaa vihreää, voi tasapainottaa tuloksena olevan kahden muun ja pitää järjestelmän tasapainossa.

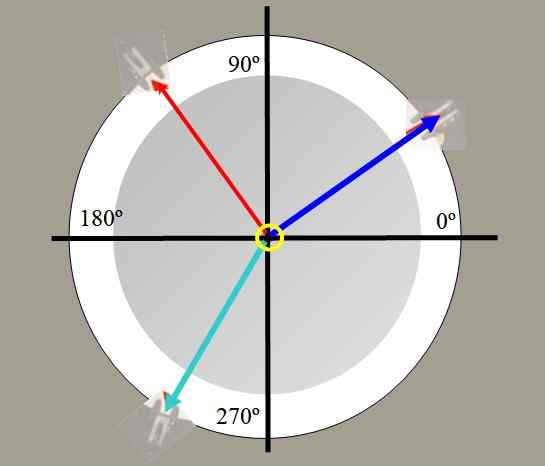Kuva 2. Näkymä Force -taulukon yläosasta. Lähde: Itse tehty.

Voimataulukon avulla voit tarkistaa voimien vektorihahmon, hajottaa voimat, löytää tasapainotusvoiman ja vahvistaa Lamyn lause:

Voi palvella sinua: aurinko

Jos Runko on tasapainossa kolmen koplanaarisen, samanaikaisen ja ei -kolineaalisen (ei -parin) voiman ansiosta, joita kutsutaan -Lla, B - ja C, Näiden voimien välinen suhde on seuraava:

A/ sin α = b/ SEN β = c/ sen γ

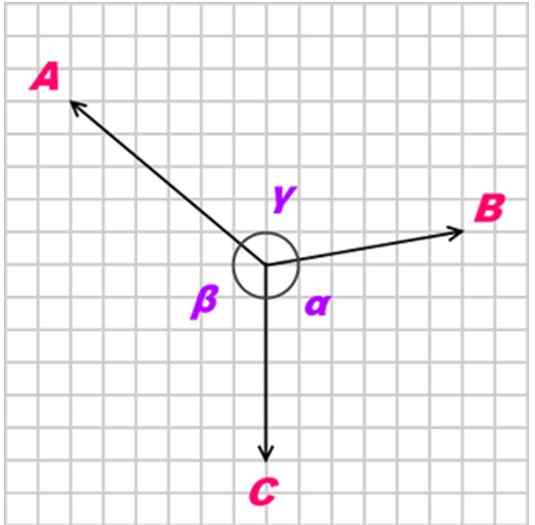Kuva 3. Lamyn lause koskee samanaikaisia ​​ja koplanaria. Lähde: Wikimedia Commons.

Ratkaisut

-Harjoitus 1

Kuvion 2 voimakkuustaulukossa painaa 225 g (sininen jännitys) ja 150 g (punainen jännitys) ripustetaan, kun kulmat esitetään. Etsi tasapainotusvoiman arvo ja kulma, jonka tämä muoto pystysuoralla akselilla.

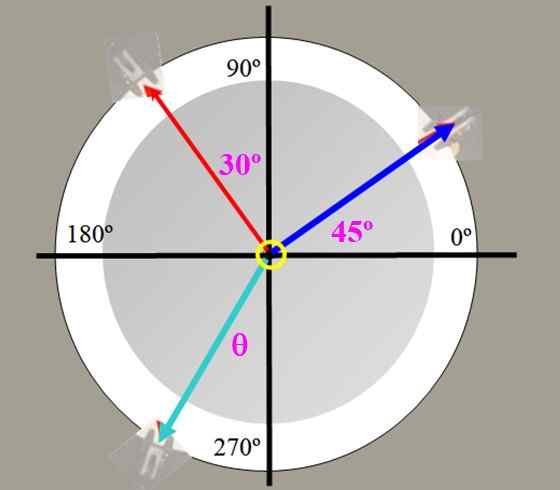Kuva 4. Forces -taulukko harjoitukselle 1.

Ratkaisu

Ongelma voidaan työskennellä grammoina ilmaistujen painoilla (voimilla). Anna p₁ = 150 grammaa ja P₂ = 225 grammaa, kunkin vastaavat komponentit ovat:

P_1x = 225 . cos 45º g = 159.10 g; P_1y = 225 . cos 45º g = 159.10 g

P_2x = -150 . SEN 30º G = -75.00 g; P_{2 ja} = 150 . Cos 30º g = 129.90 g

Tuloksena oleva paino P_{R -} Komponentit lisäävät algebrallisesti:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Tasapainotuspaino P_JA on päinvastainen vektori P_{R -}-

P_Entinen = -84.10 g

P_Hei = -289.00 g

Tasapainotuspainon suuruus lasketaan:

P_JA = (P_Entinen² + P_Hei²-A^1/2 = ((-84.10)² + (-289.00)²-A^1/2 G = 301 g

Kuvan kulma θ on:

θ = arctg (-84.10 / -289.00) = 16.2. akselin suhteen ja negatiivinen.

-Harjoitus 2

Etsi kuvassa esitetyn järjestelmän tasapainottava vektori, tietäen, että jokainen neliö mittaa 10 m puolta.

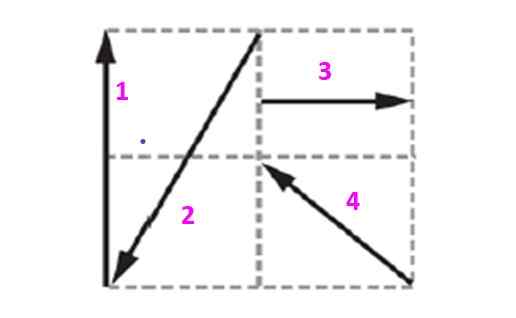Kuva 5. Kaavio esimerkistä ratkaistu 2.

Ratkaisu

Tämän ruudukon sisältämät vektorit ilmaistaan ​​yksikön ja ortogonaalisten vektorien perusteella Yllyttää ja J - jotka määrittävät tason. Vektori 1, joka merkitään v₁ Siinä on 20 metriä ja se on suunnattu pystysuoraan ylöspäin. Se voidaan ilmaista seuraavasti:

Se voi palvella sinua: säteilylämmönsiirto (esimerkeillä)

v₁ = 0 Yllyttää +kaksikymmentä J - m

Piirtämisestä havaitaan, että vektori 2 on:

v₂ = -10 Yllyttää - kaksikymmentä J - m

Vektori 3 on vaakasuora ja pisteet positiivisessa osoitteessa:

v₃ = 10 Yllyttää + 0 - J -  m

Lopuksi vektori 4 on kalteva 45 º, koska se on neliön diagonaali, joten sen komponentit mittaavat samat:

v₄ = -10 Yllyttää + 10 J - m

Huomaa, että merkki -.

Tuloksena oleva vektori saadaan lisäämällä komponentti:

v_{R -} = -10 Yllyttää + 10 J - m

Sitten järjestelmän tasapainottava vektori on:

v_JA = 10 Yllyttää - 10 J - m

Viitteet

1. Beardon, t. 2011. Johdatus vektoriin. Toipunut: Nrich.Matematiikka.org.
2. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley. 38-52.
3. Figueroa, D. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka.31-68.
4. Fyysinen. Moduuli 8: Vektorit. Toipunut: FRTL.Utn.Edu.AR
5. Hibbeler, R. 2006. Insinöörien mekaniikka. Staattinen. 6. painos. Mannertoimitusyhtiö. 15-53.
6. Lisäyslaskinvektori. Toipunut: 1728.org
7. Vektorit. Toipunut: Wikibooks.org