Ei -koplanarvektorien määritelmä, olosuhteet, harjoitukset

Se Ei -koplanaresvektorit He ovat niitä, jotka eivät jaa samaa konetta. Kaksi vapaata vektoria ja yksi piste määrittelevät yhden tason. Kolmas vektori voi jakaa kyseistä tasoa, ja jos ei, ne ovat ei -koplanarvektoreita.

Ei -katkaistuvektoreita ei voida esittää kahdessa dimensioisessa tilassa, kuten levyllä tai paperiarkilla, koska osa niistä sisältyy kolmanteen ulottuvuuteen. Edustaaksesi niitä oikein, sinun on käytettävä näkökulmaa.

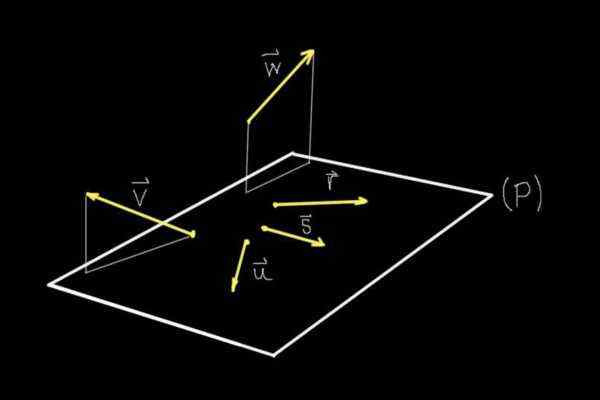Kuvio 1. Koplanares ja kytkentävektorit. (Oma yksityiskohta)

Jos tarkkailemme kuvaa 1, kaikki tiukasti esitetyt esineet ovat näytön tasossa, riippumatta siitä, että aivomme kykenevät kuvittelemaan tason (p), joka tulee samasta.

Sillä tasolla (p) ovat vektoreita r -, s, tai, kun taas vektorit v ja W -  He eivät ole siinä lentokoneessa.

Siksi vektorit r -, s, tai Ne ovat koplanarioita tai koplaaneja keskenään, koska he jakavat saman tason (p). Vektorit v ja W - He eivät jaa asunnosta minkään muun esitetyn vektorin kanssa, joten ne eivät ole kytkentä. 

[TOC]

Koplanares- ja tasoyhtälövektorit

Taso on määritelty ainutlaatuisesti, jos kolme pistettä annetaan kolmen dimensionaalisessa tilassa.

Oletetaan, että nämä kolme pistettä ovat kohta -Lla, kohta B - Ja kohta C joka määrittelee koneen (P). Näiden pisteiden kanssa on mahdollista rakentaa kaksi vektoria AB = U ja AC = V jotka ovat rakentamalla lentokoneen kanssa (P).

Näiden kahden vektorin vektori (tai ristituote) tuote johtaa niihin kolmanteen kohtisuoraan (tai normaaliin) vektoriin ja siksi kohtisuoraan tasoon nähden (P)-

n = u X v   => n ⊥ tai  ja n ⊥ v   => n ⊥ (P)    

Voi palvella sinua: Paino (fyysinen): Laskenta, yksiköt, esimerkit, harjoitukset

Kaikki muut lentokoneeseen kuuluvat kohta (P) Täytyy täyttää vektori Aq olla kohtisuorassa vektoriin n; Tämä vastaa sanomista, että skalaarituote (tai pistetuote) n kanssa Aq Sen on oltava nolla:

n Olla Aq = 0 (*)

Aikaisempi ehto vastaa sen sanomista:

Aq • (tai X v) = 0 

Tämä yhtälö varmistaa sen pisteen Q - kuulua lentokoneeseen (P). 

Kartesialainen yhtälö koneen

Aikaisempi yhtälö voidaan kirjoittaa Cartesian tavalla. Tätä varten kirjoitamme pisteiden koordinaatit -Lla, Q - ja normaalin vektorin komponentit n-

A = (a, b, c)

Q = (x, y, z)

n= (NX, NY, NZ)

Niin että AQ -komponentit ovat:

Aq= (X-A, Y-B, Z-C)

Vektorin ehto Aq olla tasossa (P) Se on nyt kirjoitettu ehto (*):

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Pistetuotteen laskeminen on edelleen:

NX (x-a) + ny (y-b) + nz (z-b) = 0

Jos se kehittää ja järjestää uudelleen, se on:

nx x + ny y + nz z = nx a + ny b + nz c

Aikaisempi lauseke on tason Cartesian yhtälö (P), normaalin vektorin komponenteista riippuen (P) ja pisteen koordinaatit -Lla joka kuuluu (P).

Olosuhteet kolmelle vektorille, jotka eivät ole koplanareja

Kuten ehto on nähty edellisessä osassa Aq • (tai X v) = 0 takaa, että vektori Aq Se on coplanario a tai ja v.

Jos soitamme W - vektoriin Aq Sitten voimme vahvistaa sen:

W -, tai ja v Ne ovat koplanareja, kyllä ​​ja vain jos W - • ( tai X v ) = 0.

Käyttäytymisen kunto

Jos kolmen vektorin kolminkertainen (tai sekoitettu tuote) tuote eroaa nollasta, nämä kolme vektoria eivät ole.

Se voi palvella sinua: Poliittisen prosessi: Ominaisuudet, sovellukset ja esimerkit

Joo    W - • ( tai X v ) ≠ 0, sitten U-, V- ja W-vektorit ovat ei-koteloita.

Jos U, V, V ja W Cartesian komponentit otetaan käyttöön, ei-käyttäytymisen tila voidaan kirjoittaa seuraavasti:

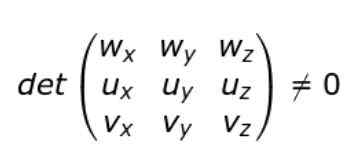Toisin sanoen, jos matriisin (3 × 3) determinantti, jonka rivet ovat U-, V- ja W-vektorien komponentteja, niin vektorit eivät ole kytkemättä.

Kolminkertaisella tuotteella on geometrinen tulkinta ja se edustaa kolmen ei -koplanaresvektorin tuottaman rinnakkaiskipien tilavuutta.

Kuva 2. Kolme ei-kytkentävektoria määrittelevät rinnakkaisepipedon, jonka tilavuus on kolminkertainen tuotesäke. (Oma yksityiskohta)

Syynä on seuraava; Kun kaksi ei-kytkentävektoria on moninkertaistunut. 

Sitten kun tämä vektori on moninkertainen. 

Toisin sanoen, sinulla on yhdensuuntainen yhdensuuntainen alue, joka on muodostettu kahden ensimmäisen kerrottuna kolmannen vektorin korkeudella.

Vaihtoehtoinen tila kytkemättä

Jos sinulla on kolme vektoria ja mitä tahansa niistä ei voida kirjoittaa kahden muun lineaarisena yhdistelmänä, niin kolme vektoria eivät ole peittäviä. Se on kolme vektoria tai, v ja W - Ne eivät ole peittäviä, jos ehto:

α tai + β v + γ W - = 0

Se täyttyy vain, kun α = 0, β = 0 ja γ = 0.

Ratkaisut

-Harjoitus 1

Sinulla on kolme vektoria

tai = (-3, -6, 2);   v = (4, 1, 0) ja W - = (-1, 2, z)

Huomaa, että vektorin Z -komponentti W - Se on tuntematon.

Löydä arvoalue, jonka Z voi ottaa niin, että taataan, että kolme vektoria eivät jaa samaa tasoa.

Voi palvella sinua: Vakaa tasapaino: Konsepti ja esimerkit

Ratkaisu 

Käytämme uudelleen kolmen vektorin joukkojen muodostaman matriisin määräävän matriisin kriteeriä, tällä tavoin jäljellämme: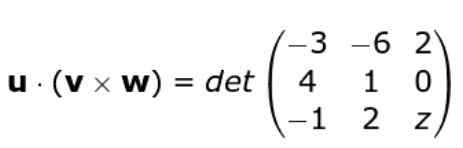Kehitämme determinantin

W - • ( tai X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3Z + 24z + 18 = 21z + 18

Sovitamme tämän lausekkeen nolla -arvolla

21 z + 18 = 0

Ja tyhjennämme z

Z = -18/21 = -6/7

Jos muuttuja z ottaisi arvon -6/7, niin kolme vektoria olisivat koplanares.

Niin, että z: n arvot, jotka takaavat vektorit, eivät ole, ovat seuraavat aikavälillä:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Harjoitus 2

Etsi seuraavassa kuvassa esitetyn rinnakkaiskipien tilavuus:

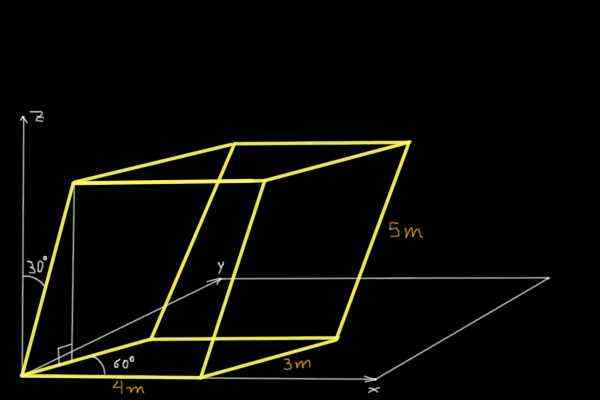
Ratkaisu 

Kuvassa esitetyn rinnakkaiskipien tilavuuden löytämiseksi kolmen ei-concurrent-kytkentävektorin kartesian komponentti määritetään koordinaattijärjestelmän alkuperässä. Ensimmäinen on vektori tai  4m ja yhdensuuntainen x -akselin kanssa:

tai= (4, 0, 0) m

Toinen on vektori v XY 3M -kokoisessa tasossa, joka muodostaa 60º X -akselin kanssa:

v= (3*cos 60º, 3*Sen 60º, 0) = (1.5, 2.6, 0.0) m

Ja kolmas vektori W - 5 m ja jonka projektio XY -tasossa muodostuu 60º X -akselilla, lisäksi w muodostuu 30º z -akselin kanssa.

W -= (5*sin 30º*cos 60º, 5*sen 30º*sin 60º, 5*Sen 30º)

Suoritti laskelmat: W -= (1.25, 2.17, 2.5m.

Viitteet

1. Figueroa, D. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. 31-68.
2. Fyysinen. Moduuli 8: Vektorit. Toipunut: FRTL.Utn.Edu.AR
3. Hibbeler, R. 2006. Insinöörien mekaniikka. Staattinen. 6. painos. Mannertoimitusyhtiö.28-66.
4. McLean, W. Schaum -sarja. Insinöörien mekaniikka: staattinen ja dynaaminen. Kolmas painos. McGraw Hill. 1-15.
5. Wikipedia. Vektori. Palautettu: se on.Wikipedia.org