Suhteellinen nopeuskonsepti, esimerkit, harjoitukset

Se Suhteellinen nopeus esine on sellainen, joka mitataan tietyn tarkkailijan suhteen, koska toinen tarkkailija voi saada toisen toimenpiteen. Nopeus riippuu aina tarkkailijasta, joka mittaa sitä.

Siksi tietyn henkilön mittaaman esineen nopeus on suhteellinen nopeus suhteessa siihen. Toinen tarkkailija voi saada erilaisen arvon nopeudelle, silti saman esineen tapauksessa.

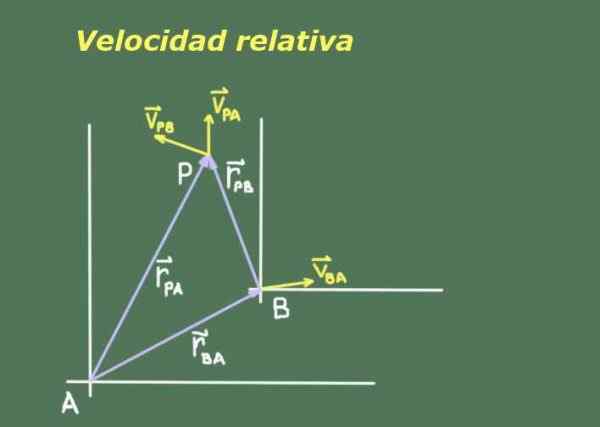
Kuvio 1. Kaavio, joka edustaa pistettä P, nähdään referenssijärjestelmistä A ja B. Lähde: Itse tehty.

Kaksi tarkkailijaa A ja B, jotka liikkuvat toisistaan, heillä voi olla erilaisia ​​mittauksia kolmannesta P -objektista, joka liikkuu, on tarpeen etsiä suhde A: n sijaintien ja P -näkymien nopeuksien välillä.

Kuvio 1 esittää kahta tarkkailijaa A ja B vastaavien vertailujärjestelmien kanssa, joista ne mittaavat esineen P sijainnin ja nopeuden.

Jokainen tarkkailija A ja B mittaa esineen P sijainnin ja nopeuden tietyllä hetkellä t. Klassisessa suhteellisuudessa (tai Galilean) tarkkailijan A aika on sama kuin tarkkailijan B suhteellisesta nopeudesta riippumatta.

Tämä artikkeli koskee klassista suhteellisuutta, joka on pätevä ja sovellettavissa useimpiin arjen tilanteisiin, joissa esineillä on paljon pienemmät nopeudet kuin valossa.

Tarkkailijan B sijainti merkitsee r -_Ba. Koska sijainti on vektorisäki, käytämme lihavoitua sen osoittamiseen. Esineen P sijainti osana r -_Paa ja saman esineen p b: n suhteen r -_Pb.

[TOC]

Sijaintien ja suhteellisten nopeuksien välinen suhde

Näiden kolmen aseman välillä on vektorisuhde, joka voidaan päätellä kuvan 1 esityksestä:

 r -_Paa= r -_Pb + r -_Ba

Jos edellinen ilmaisu otetaan aikaan ajankohtana t Saamme kunkin tarkkailijan suhteellisen nopeuden välisen suhteen:

Voit palvella sinua: Newtonin toinen laki: sovellukset, kokeet ja harjoitukset

V_Paa= V_Pb + V_Ba

Edellisessä lausekkeessa on P: n suhteellinen nopeus A: n suhteen P: n suhteellisesta nopeudesta suhteessa B: hen ja B: n suhteellinen nopeus suhteessa suhteessa.

Samoin P: n suhteellinen nopeus voidaan kirjoittaa suhteessa P: n suhteelliseen nopeuteen suhteessa A ja B: n suhteellinen nopeus.

V_Pb= V_Paa + V_Ab

On huomattava, että B: n suhteellinen nopeus on tasa -arvoinen ja vastoin B: n suhteen A: A: n suhteen:

V_Ab = -V_Ba 

Tätä näkyy liikkuvasta autosta

Auto kulkee suoraa tietä, joka menee lännestä tähän, nopeasti 80 km/h vastakkaiseen suuntaan (ja toisella kaistalla) tulee moottoripyörä nopeasti 100 km/h.

Auton takaistuimessa kulkee lapsen, joka haluaa tietää häntä lähestyvän moottoripyörän suhteellisen nopeuden. Saadaksesi vastauksen, lapsi soveltaa juuri edellisessä osassa lukemasi suhteet tunnistaen jokaisen koordinaattijärjestelmän seuraavasti:

-A on tiellä olevan tarkkailijan koordinaattijärjestelmä ja sen suhteen kunkin ajoneuvon rapides on mitattu.

-B on auto ja p on moottoripyörä.

Jos haluat laskea Moto P: n nopeuden, Auton B suhteen seuraavaa suhdetta käytetään:

V_Pb= V_Paa + V_Ab=V_Paa - V_Ba

Ottaen yhtä positiivisesti länsi-idän suuntaan, jonka sinulla on:

V_Pb= (-100 km/h - 80 km/h) Yllyttää = -180 km/h Yllyttää

Tämä tulos tulkitaan seuraavasti: moottoripyörä liikkuu suhteessa autoon nopeudella 180 km/h ja suunta -Yllyttää, Toisin sanoen tämä länteen.

Se voi palvella sinua: Block Algebra: elementit, esimerkit, ratkaisut harjoitukset

Suhteellinen nopeus moottoripyörän ja auton välillä

Moottoripyörä ja auto ovat ylittäneet jokaisen kaistansa jälkeen. Poika, joka menee auton takapenkillä, näkee moottoripyörän pois ja haluaa nyt tietää, millä nopeudella hän liikkuu hänestä, olettaen, että sekä moottoripyörä että auto ylläpitävät samoja rapidesia kuin ennen ylittämistä.

Lapsi soveltaa vastausta, jota aikaisemmin käytettiin:

V_Pb= V_Paa + V_Ab=V _Paa - V_Ba

V_Pb= -100 km/h Yllyttää - 80 km/h Yllyttää = -180 km/h Yllyttää

Ja nyt moottoripyörä siirtyy autosta samalla suhteellisella nopeudella, jonka kanssa he lähestyivät ennen kuin he ylittivät.

Sama osan 2 moottoripyörä palaa pitämällä saman nopeutensa 100 km/h, mutta muuttamalla sen osoitetta. Toisin sanoen auto (joka jatkuu nopeasti 80 km/h) ja moottoripyörä molemmat liikkuvat positiiviseen suuntaan.

Yhdessä vaiheessa moottoripyörä ylittää auton, ja auton takaistuimella kulkeva lapsi haluaa tietää moottoripyörän suhteellisen nopeuden suhteessa häneen, kun hän näkee hänen ohi hänen vierellään.

Vastauksen saamiseksi lapsi soveltaa uudelleen suhteellisen liikkeen suhteita:

V_Pb= V_Paa + V_Ab=V_Paa - V_Ba

V_Pb= +100 km/h Yllyttää - 80 km/h Yllyttää = 20 km/h Yllyttää 

Takaistuimen lapsi tarkkailee moottoripyörää, joka edistää autoa nopeudella 20 km/h.

-Liikuntaa

Harjoitus 1

Moottorivene ylittää 600 metrin leveän joen ja virtaa pohjoisesta etelään. Joen nopeus on 3 m/s. Veneen nopeus joen veteen on 4 m/s itään.

Voi palvella sinua: klassisen ja modernin fysiikan haarat

(i) Löydä veneen nopeus Riverbankin suhteen.

(ii) Ilmoita veneen nopeus ja suunta maan suhteen.

(iii) Laske ylitymisaika.

(iv) kuinka paljon on siirtynyt etelään lähtökohtaan.

Ratkaisu 

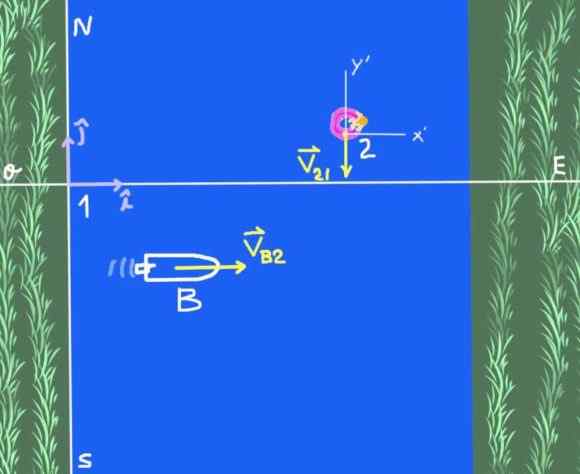Kuva 2. Veneen ylitys joen (harjoitus 1). Lähde: Itse tehty.

Vertailujärjestelmiä on kaksi: Riverbankin solidaarisuusviitejärjestelmä, jota kutsumme 1 ja vertailujärjestelmä 2, joka on tarkkailija, joka kelluu joen vedessä. Tutkimuksen kohde on vene B.

Veneen nopeus joen suhteen on kirjoitettu vektorimuodossa seuraavasti:

VB2 = 4 Yllyttää neiti

Tarkkailijan 2 nopeus (lautta joen yli) suhteessa tarkkailijaan 1 (maalla):

Vkaksikymmentäyksi = -3 J - neiti

Haluat löytää veneen nopeuden maalle VB1.

VB1 = VB2 + Vkaksikymmentäyksi

Vastaa i

VB1 = (4 Yllyttää - 3 J -) neiti   

Veneen nopeus on edellinen nopeusmoduuli:

JaVB1Ja = (42 + (-3) 2) ½ = 5 m/s

Vastaus II

Ja osoite on:

θ = Arcan (-¾) = -36,87º 

Vastaus III

Veneen ylitysaika on joen leveyden ja veneen nopeuden komponentin X välinen suhde maan suhteen.

T = (600 m)/(4 m/s) = 150 s 

Vastaus IV

Veneen eteläisen ajautumisen laskemiseksi komponentti ja veneen nopeus suhteessa maahan kerrotaan risteykseen:

d -d = -3 J - m/s * 150 s = -450 J - m

Siirtymä etelään lähtökohtaan nähden on 450 metriä.

Viitteet

1. Giancoli, D. Fysiikka. Periaatteet hakemuksissa. 6. painos. Prentice Hall. 80-90
2. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 100-120.
3. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Painos. Meksiko. Cengage Learning Editors. 95-100.
4. Wikipedia. Suhteellinen nopeus. Toipunut: Wikipedia.com
5. Wikipedia. Suhteellinen nopeusmenetelmä. Toipunut: Wikipedia.com