Mekaaninen etukaava, yhtälöt, laskelmat ja esimerkit

Se Mekaaninen etu Se on ulottumaton tekijä, joka kvantifioi mekanismin kyvyn monistaa - joissakin tapauksissa vähenee - sen läpi kohdistettu voima. Konseptia sovelletaan mihin tahansa mekanismiin: saksista urheiluauton moottoriin.

Ajatuksena on, että kone muuttaa voiman, jota käyttäjä käyttää sitä paljon suuremmalla voimalla kuin edustaa hyötyä, tai vähentää sitä herkän tehtävän suorittamiseksi.

Kuvio 1. Hydraulinen hissi on kone, jonka mekaaninen etu on suurempi kuin 1. Lähde: Pixabay.

Muista, että mekanismin toiminnassa osa sovelletusta voimasta on väistämättä investoida kitkan torjuntaan. Siksi mekaaninen etu luokitellaan todelliseksi mekaaniseksi etuksi ja ihanteelliseksi mekaaniseksi etuna.

[TOC]

Määritelmä ja kaavat

Koneen todellinen mekaaninen etu määritellään syynä koneen kohdistaman voiman suuruuden välillä kuormitukseen (lähtövoima) ja koneen käyttämiseen tarvittava voima (tulovoima):

Todellinen mekaaninen etu VMR = lähtövoima/tulovoima

Vaikka ihanteellinen mekaaninen etu riippuu etäisyydestä, joka kulkee syöttövoiman läpi ja poistumisvoiman läpi kulkevasta:

Ihanteellinen mekaaninen etu VMI = tuloetäisyys/lähtöetäisyys

Molemmat edut ovat osia määrien välillä, joilla on samat ulottuvuudet, ne ovat ulottumattomia (ilman yksiköitä) ja myös positiivisia.

Monissa tapauksissa, kuten kuorma -auto ja hydraulinen puristus, mekaaninen etu on suurempi kuin 1, ja toisissa mekaaninen etu on vähemmän kuin 1, esimerkiksi kalastusruokissa ja pinsetteissä.

Ihanteellinen VMI -mekaaninen etu

VMI liittyy mekaaniseen työhön, joka suoritetaan koneen sisäänkäynnillä ja poistumisessa. Sisäänkäynnin työ, jota kutsumme w_Yllyttää, Se jaotellaan kahteen komponenttiin:

Voi palvella sinua: Doppler -vaikutus: Kuvaus, kaavat, tapaukset, esimerkit

W -_Yllyttää = Työskentely kitkan + lähtötyön voittamiseksi

Ihanteellisen koneen ei tarvitse tehdä työtä kitkan voittamiseksi, joten pääsytyö olisi sama kuin tuotoksen, nimeltään W_jompikumpi-

Työskentele sisäänkäynnillä = työskentele tulossa → W_Yllyttää = W_jompikumpi.

Koska tässä tapauksessa työ on etäisyyden voimaa, sinulla on: w_Yllyttää = F_Yllyttää . s_Yllyttää

Missä f_Yllyttää ja s_Yllyttää Alkuperäinen voima ja etäisyys ovat vastaavasti. Lähtötyö ilmaistaan ​​analogisesti:

W -_jompikumpi= F_jompikumpi . s_jompikumpi

Tässä tapauksessa f_jompikumpi ja s_jompikumpi ovat vahvuus ja etäisyys, jonka kone toimittaa vastaavasti. Nyt molemmat teokset vastaavat:

F_Yllyttää . s_Yllyttää = F_jompikumpi . s_jompikumpi

Ja tulos voidaan kirjoittaa uudelleen voimien ja etäisyyksien osuus:

(S_Yllyttää /s_jompikumpi) = (F_jompikumpi /F_Yllyttää-A

Juuri etäisyyssuhde on ihanteellinen mekaaninen etu, alussa annetun määritelmän mukaan:

VMI = S_Yllyttää /s_jompikumpi

Tehokkuus tai koneen suorituskyky

On kohtuullista miettiä molempien teosten välisen muutoksen tehokkuutta: sisäänkäynnin ja lähtö. Merkitsemällä miten ja Tehokkuuteen tämä määritellään seuraavasti:

E = lähtötyö /sisäänkäynti = W_jompikumpi /W_Yllyttää = F_jompikumpi . s_jompikumpi / F_Yllyttää . s_Yllyttää

Tehokkuus tunnetaan myös mekaanisena suorituskyvynä. Käytännössä poistumistyö ei koskaan ylitä pääsyä kitkahäviöiden vuoksi, joten jakaminen ja Se ei ole enää yhtä suuri kuin 1, mutta vähemmän.

Vaihtoehtoinen määritelmä sisältää voiman, joka on aika yksikköä kohti:

E = lähtöteho /syöttöteho = P_jompikumpi /P_Yllyttää

Todellinen mekaaninen etu VMR

Todellinen mekaaninen etu määritellään yksinkertaisesti tulosvoiman F väliseksi suhde_jompikumpi ja tulo f_Yllyttää-

Vmr = f_jompikumpi/F_Yllyttää

VMI: n, VMR: n ja tehokkuuden välinen suhde

Tehokkuus ja Se voidaan kirjoittaa uudelleen VMI: n ja VMR: n suhteen:

Voi palvella sinua: Lämpölaajennus

e = f_jompikumpi . s_jompikumpi / F_Yllyttää . s_Yllyttää  = (F_jompikumpi /F_Yllyttää-A.(S_jompikumpi/s_Yllyttää) = VMR /VMI

Siksi tehokkuus on osamäärä todellisen mekaanisen edun ja ihanteellisen mekaanisen edun välillä, joka on ensimmäinen alempi kuin toinen.

VMR -laskenta tietäen tehokkuuden

Käytännössä VMR lasketaan määrittämällä tehokkuus ja tuntemalla VMI:
VMR = E. VMI

Kuinka mekaaninen etu lasketaan?

Mekaanisen edun laskeminen riippuu konetyypistä. Joissakin tapauksissa on kätevää kuljettaa sitä voimien siirron kautta, mutta muun tyyppisissä koneissa, kuten esimerkiksi hihnapyörissä, vääntömomentti tai vääntömomentti τ on.

Tässä tapauksessa VMI lasketaan vastaamalla hetkiä:

Lähtö vääntömomentti = tulon vääntömomentti

Vääntömomentin suuruus on τ = f.r -.synti θ. Jos voima ja sijaintivektori ovat kohtisuorassa, niiden välillä on kulma 90º ja Sen θ = Sen 90º = 1, saadaan:

F_jompikumpi . r -_jompikumpi = F_Yllyttää . r -_Yllyttää

Mekanismeissa, kuten hydraulisessa puristimessa, joka koostuu kahdesta kamerasta, jotka on kytketty poikittaisputken avulla ja täynnä nestettä, paine voi siirtyä mäntäillä, jotka liikkuvat vapaasti jokaisessa kammiossa. Tällöin VMI lasketaan:

Poistumispaine = paine syötteenä

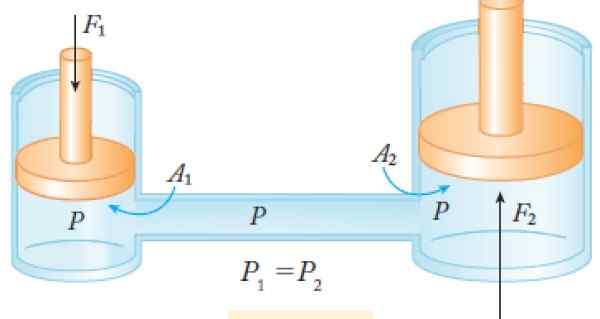Kuva 2. Hydraulinen puristusjärjestelmä. Lähde: Cuéllar, J. 2015. Fysiikka II. McGraw Hill.

Esimerkit

- Esimerkki 1

Vipu koostuu ohuesta palkista, jota tukee Fulcro, joka voidaan sijoittaa monin tavoin. Kun levitetään tiettyä voimaa, nimeltään "voimanvoima", se vanhenee sen kanssa paljon suurempi, mikä on taakka jompikumpi kestävyys.

Kuva 3. Ensimmäisen luokan vipu. Lähde: Wikimedia Commons. CR [CC BY-S (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Fulcro, sähkövoimaa ja kuormaa mekaanisen edun saavuttamiseksi on olemassa useita tapoja. Kuvio 3 esittää ensimmäisen luokan vipua, samanlainen kuin keinu, Fulcro sijaitsee sähkövoiman ja kuorman välissä.

Voi palvella sinua: vino parabolinen laukaus: Ominaisuudet, kaavat, yhtälöt, esimerkit

Esimerkiksi kaksi eri painoa henkilöä voi olla tasapainossa rokkarissa tai ylös ja alas Jos he istuvat riittävällä etäisyydellä fulcrosta.

Ensimmäisen asteen vivun VMI: n laskemiseksi, koska käännöstä tai kitkaa ei ole, mutta kierto, hetket vastaavat, tietäen, että molemmat voimat ovat kohtisuorassa palkkiin asti. Täällä f_Yllyttää on sähkövoima ja f_jompikumpi Se on kuorma tai vastus:

F_jompikumpi . r -_jompikumpi = F_Yllyttää . r -_Yllyttää

F_jompikumpi /F_Yllyttää  = r_Yllyttää / r_jompikumpi

Määritelmän mukaan VMI = F_jompikumpi /F_Yllyttää , niin:

VMI = R_Yllyttää / r_jompikumpi

Kitkan puuttuessa: VMI = VMR. Huomaa, että VMI voi olla suurempi tai vähemmän kuin 1.

- Esimerkki 2

Hydraulisen puristimen ihanteellinen mekaaninen etu lasketaan paineen kautta, joka Pascal -periaatteen mukaan siirretään kokonaan säiliössä rajoitetun nesteen kohtiin.

Syöttövoima f₁ Kuviossa 2 sitä levitetään pienessä männässä₁ vasemmalla ja poistumisvoima F₂ Se saadaan alueen A suuresta männästä₂ oikealla. Niin:

Syöttöpaine = lähtöpaine

Paine määritellään voimana alueyksikköä kohti, siksi:

(F₁ /₁) = (F₂ /₂) → a₂ /₁  = F₂ / F₁ 

Koska vmi = f₂ / F₁, Sinulla on mekaaninen etu alueiden välillä: alueiden välillä:

VMI = A₂ /₁

Kuten₂ > A₁, VMI on suurempi kuin 1 ja puristimen vaikutuksena on kertoa pienessä männässä F voima₁.

Viitteet

1. Cuéllar, j. 2009. Fysiikka II. Ensimmäinen. Painos. McGraw Hill.
2. Kane, J. 2007. Fyysinen. Toinen. Painos. Toimitus palautti.
3. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill
4. Wikipedia. Vipu. Palautettu: on.Wikipedia.org.
5. Wikipedia. Mekaaninen etu. Palautettu: on.Wikipedia.org.