X neliö

Selitämme, mikä on x neliö, sen ominaisuudet, esimerkit ja harjoitukset ratkaistu

"X" -puolen neliön pinta -ala on X Squared. Lähde: f. Zapata.

"X neliö"Se suoritetaan kertomalla määrä" x "itsensä kanssa kahdesti. Se on osa potentiaatiooperaatioita, ja matemaattisissa symboleissa se ilmaistaan ​​tällä tavalla:

x ∙ x = x²

Tämä on erityinen vaikutusmahdollisuuksien tapaus, jossa "x" edustaa pohja Ja "2" on eksponentti. Jos operaatiossa termi x ilmestyy², Se lukee tarkalleen "x neliö" tai "x neliö korotettu".

Luonnollisesti muut eksponentit ovat mahdollisia, esimerkiksi jos eksponentti on 3, niin virta kirjoitetaan seuraavasti:

x ∙ x ∙ x = x³

Ja lue nimellä "x kolmeen", "x nostettu kuutioon" tai yksinkertaisesti "x kuutioon".

Yleensä eksponentti, jolle pohja on korkea, voi olla mikä tahansa luku, nimeltään "N", ja siinä tapauksessa vastaava voima on kirjoitettu:

xⁿ = x ∙ x ∙ x ∙… ∙ x

Täällä keskeiset kohdat osoittavat, että ”x” on kerrottava itsessään "n", toisin sanoen niin monta kertaa kuin eksponentti osoittaa sen.

Joitakin yksinkertaisia ​​esimerkkejä "X Squared" -numeroista ovat seuraavat:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Myöhemmin kuvataan erilaisia ​​sovelluksia, joille se on välttämätöntä.

Potentiaatioominaisuudet

Yleensä minkä tahansa määrän tuote itsensä kanssa, N kertaa, sitä kutsutaan potentiaatioksi. X -neliön laskenta on vain tietty potentiaatiotapaus, kaksi muuta tapausta ilmestyy, kun haluat nostaa määrän eksponentteja 1, mikä saa seurauksena saman määrän:

Voi palvella sinua: Eksponenttien lait

Koska nämä toiminnot ovat usein, toimimaan tukikohtien ja eksponenttien kanssa, noudatetaan joitain yksinkertaisia ​​toimintasääntöjä, nimeltään Eksponenttien laki, jotka on lueteltu alla:

Eksponenttien laki

Seuraavassa "X" on pohja ja "N" ja "M" ovat eksponentteja.

1.- Tasavertaiset perusvoimat

Kertomalla kaksi (tai useampaa) yhtä suurta emäksistä voimaa, saadaan emäksen summalle nostettu pohja:

xⁿ∙ x^m = x^n+m

X High -tapauksessa tätä sääntöä sovelletaan seuraavasti, korvaamalla N ja M 1: lle:

x¹∙ x¹ = x¹⁺¹ = x²

2.- Tasa -arvon jakautuminen tasavertaiseen tukikohtaan

Jakamalla saman emäksen voimat, pohja saadaan, nostetaan vähennykseen vastaavien osoittajan ja nimittäjän välillä:

xⁿ ÷ x^m = x^N-m

Koska osastoa 0: lla ei ole määritelty, se on täytettävä, mikäli x ≠ 0.

3.- Voimanvoima

Voiman tehon tulos on yhtä suuri kuin eksponenttien tuotteen kohotettu pohja:

(x^m-Aⁿ = x^m∙n

Se voidaan saada uudelleen x -neliöön, kun teet M = 1 ja n = 2:

(x¹-A² = x^1∙2 = x²

4.- Negatiivinen eksponentti

Negatiivisten eksponenttien suoritettava operaatio on:

Aina kun x ≠ 0. Huomaa, että tässä tapauksessa tehosta tulee murto -osa, jonka osoittaja on yhtä suuri kuin 1.

5.- Murto -eksponentti

Murtolaiset eksponentit voidaan kirjoittaa pohjan n. Juurena:

Ehdolla, että n on erilainen kuin 0. Tästä arvosta tulee juurihakemisto, kun taas M: stä tulee juuren alla olevan määrän eksponentti, joka tässä tapauksessa on x.

Voi palvella sinua: mikä on ohje? (Geometria)

Eri emäksen tuotteet ja osuudet

Kun sinun on parannettava erilaisia ​​"X" ja "Y" -tuotteita ja osuuksia, näitä sääntöjä noudatetaan:

1.- Tuotevirta

Tämän voiman suorittamiseksi jokainen määrä nostetaan eksponentti N: lle ja tuloksena oleva tuote on perustettu:

(x ∙ y)ⁿ = xⁿ ⋅ jaⁿ

2.- Osamäärän suhde

Jälleen jokainen määrä on nostettava eksponentti N: lle erikseen ja määritettävä jakaminen, joka johtaa säännön mukaisesti, että määrä "y" on erilainen kuin 0, positiivisen “n” tapauksessa:

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

Kun "N" on negatiivinen, varovaisuus on otettava huomioon edellisen jakson omaisuuden 4 vuoksi, numeraattorista tulee nimittäjä. Tässä tapauksessa molempien määrien on oltava erilainen kuin 0, koska jaostoa 0: lla on vältettävä hinnalla millä hyvänsä.

Esimerkit

Esimerkki 1: Luonnollisten lukujen neliöt

Kymmenen ensimmäisen luonnollisen numeron neliöt ovat:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Esimerkki 2: Negatiivisten lukujen neliö

Negatiivisen luvun neliö on aina positiivinen, koska kaksi yhtä suurta merkkiä määrää kerrotaan, siksi:

(-x) · (-x) = x ∙ x = x²

Esimerkiksi:

(-2) · (-2) = (-2)² = 4

Esimerkki 3: Summan ja eron neliö

Usein on tarpeen laskea kahden määrän summa tai sen ero, toiminnot, jotka sisältyvät merkittävien tuotteiden luokkaan.

Operaatio ratkaistaan ​​annetuilla indikaatioilla ja jakavan ominaisuuden avulla:

Summa

Olkoon kaksi "x" ja "y" -määrää, ja haluat löytää sen summan neliön (x + y)²-

Voi palvella sinua: operaatiohierarkia

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + ja²

Tämä lauseke lukee näin: "Ensimmäisen neliön neliö, plus ensimmäisen tuote toisen toisen plus toisen neliön".

Eron neliö

Se on ratkaistu analogisesti, mutta ottaen huomioon negatiivinen merkki:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ ja + ja²

Esimerkki 4: Neliön pinta -ala

Neliö on 4 -puolinen monikulmio, jolla on sama mitta. Olkoon ℓ sivumittaus, sitten hahmon alue A on annettu:

A = ℓ²

Esimerkki 5: Pythagoras -lause

Tämä lause koskee suorakaiteen kolmioita, jotka kaksi sen sivuista muodostavat suoran kulman. Nämä puolet tunnetaan nimellä "luokat" ja jäljellä oleva puoli on "hypotenuse".

Lause osoittaa, että hypotenusan neliö on yhtä suuri kuin luokkien neliöiden summa. Kutsutaan "A" ja "B" luokkiin ja "C" hypotenuseen, lause on kirjoitettu seuraavasti:

c² = a² + b -²

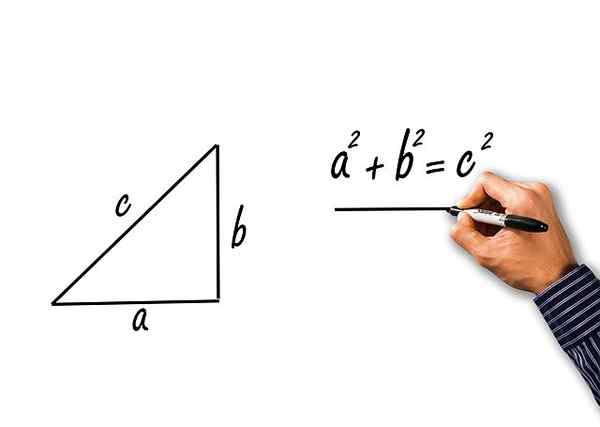Pythagoras -lause kissojen A ja B suorakulmion kolmiolle ja hypotenusa c

Ratkaisut

Harjoitus 1

Laske hypotenusen neliö, jonka jalat mittaavat 3 ja 5 yksikköä.

Ratkaisu

Pythagorasin lauseen mukaan hypotenusen neliö on:

c² = a² + b -²

Arvojen korvaaminen:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Harjoitus 2

Määritä sivun neliön pinta -ala ℓ = 6 cm

Ratkaisu

A = ℓ² = (6 cm)² = 36 cm²