Centripetaalin kiihtyvyys määritelmä, kaavat, laskelmat, harjoitukset

Se centripetaalinen kiihtyvyys -lla_c, Kutsutaan myös radiaaliseksi tai normaaliksi, kiihtyvyys kantaa liikkuvaa objektia kuvaamalla ympyrätietä. Hänen suuruus on v²/r, missä r - Se on ympyrän säde, se on suunnattu kohti sen keskustaa ja vastaa siitä, että matkapuhelin pysyy reitillä.

Centripetaalin kiihtyvyyden mitat ovat pituisia yksikköä kohti. Kansainvälisessä järjestelmässä he ovat m/s². Jos jostain syystä centripetaalinen kiihtyvyys katoaa, niin myös lujuus, joka pakottaa liikkuvan ylläpitämään pyöreän radan ylläpitämistä.

Pyöristävillä esineillä on keskitetyn kiihtyvyys, joka on suunnattu kohti radan keskustaa. Lähde: Pixabay

Näin tapahtuu autolle, joka yrittää antaa käyrän tasaisella ja pakkasella, jossa lattian ja pyörien välinen kitka on riittämätön niin, että auto vie käyrän. Siksi ainoa mahdollisuus, jonka olet lähtenyt, on liikkua suorassa linjassa, ja siksi pääset ulos käyrästä.

[TOC]

Pyöreät liikkeet

Kun esine liikkuu ympyrässä, centripetaalinen kiihtyvyys on aina suunnattu ympärysmiipan keskipisteeseen, suunta, joka on kohtisuorassa seurataan.

Koska nopeus on aina tangentti etenemissuunnassa, niin nopeus ja centripetaalinen kiihtyvyys osoittautuvat kohtisuoraan. Siksi nopeudella ja kiihtyvyydellä ei aina ole samaa suuntaa.

Näissä olosuhteissa matkapuhelimella on mahdollisuus kuvata ympärysmitta vakiona tai muuttuvan nopeuden avulla. Ensimmäinen tapaus tunnetaan yhtenäisenä tai MCU -ympyräliikkeinä lyhenteeltään, toinen tapaus on muuttuva pyöreä liike.

Se voi palvella sinua: mikä on päästöpyyhe? (Esimerkkejä)

Molemmissa tapauksissa centripetaalinen kiihtyvyys on vastuussa liikkuvan kiertämisen pitämisestä, miehittäen, että nopeus vaihtelee vain suunnassa ja suunnassa.

Muuttuvan pyöreän liikkeen saamiseksi tarvitaan kuitenkin toinen kiihtyvyyden komponentti samaan nopeuteen, mikä vastaa nopeuden lisäämisestä tai pienenemisestä. Tämä kiihtyvyyskomponentti tunnetaan nimellä Tangentiaalinen kiihtyvyys.

Muuttuvalla pyöreällä liikkeellä ja kaarevalla liikkeellä on yleensä kiihtyvyyden molemmat komponentit, koska kaareva liike voi kuvitella reitin lukemattomien ympäryskaarien läpi, jotka muodostavat kaarevan radan.

Centripetaalinen voima

Nyt joukko on vastuussa kiihtyvyyden tarjoamisesta. Maata kiertää satelliittia, se on painovoiman voima. Ja koska painovoima toimii aina kohtisuorassa etenemissuunnassa, se ei muuta satelliitin nopeutta.

Tässä tapauksessa painovoima toimii a keskihakuvoima, että se ei ole erityinen luokka tai voiman lisäksi, vaan se, joka satelliitin tapauksessa on suunnattu säteittäisesti kohti maan keskustaa.

Muun tyyppisissä pyöreissä liikkeissä, esimerkiksi käyrällä, joka kulkee käyrän, centripetaalivoiman roolia tulkitaan staattisella RUBB -voimalla, joka pakottaa liikkuvan kääntymään.

Centripetaalin kiihtyvyyden kaavat

Centripetaalinen kiihtyvyys lasketaan lausekkeella:

AC = v²/r

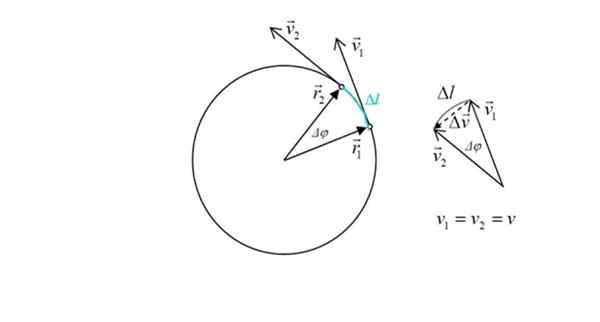Kaavio Centripetaalin kiihtyvyyden laskemiseksi matkapuhelimessa MCU: n kanssa. Lähde: Lähde: Ilevanat [CC BY-Sa 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Tämä ilmaus johdetaan alla. Määritelmän mukaan kiihtyvyys on ajan nopeuden vaihtelu:

Se voi palvella sinua: valonlähteet: tyypit ja laitteet, jotka säteilevät valoa

Yläkaavio näkyy vasemmassa kuvassa, kaksi pistettä, joiden läpi matkapuhelin kulkee radiopiirissä r - antihorarium -mielessä. Huomaa, että nopeuden suuruus on sama molemmissa tapauksissa, mutta ei suunta tai merkitys.

Matkapuhelin käyttää aikaa δt Kiertueella, joka on pieni, koska pisteet ovat hyvin lähellä.

Kuvassa on myös kaksi sijainvektoria r -₁ ja r -₂, Kenen moduuli on sama: radio r - ympärysmitta. Molempien pisteiden välinen kulma on Δφ. Vihreällä keula- Kiertue matkapuhelimeen, nimeltään ΔL.

Oikealla olevassa kuvassa nähdään, että δ: n suuruusv, Nopeuden muutos on suunnilleen verrannollinen ΔL: ään, koska kulma Δφ on pieni. Mutta nopeuden muutos liittyy juuri kiihtyvyyteen. Kolmioa varoitetaan vektoreiden summan perusteella, että:

v₁ + Δv = v₂ → ΔV = V₂ - v₁

Δv Se on mielenkiintoista, koska se on verrannollinen centripetaaliseen kiihtyvyyteen. Kuviosta varoitetaan, että pieni kulma Δφ, vektori δv Se on kohtisuorassa olemuksessa molemmat v₁ Kuten v₂ ja osoittaa kehän keskustaan.

Vaikka vektorit erottuvat lihavoituna, seuraavien geometrisen luonteen vaikutuksille työskentelemme näiden vektoreiden moduulien tai suuruuksien kanssa vektorimerkinnästä riippumatta.

Jotain muuta: Sinun on käytettävä keskikulman määritelmää, mikä on:

Δφ= Δl/r

Nyt molempia lukuja verrataan, jotka ovat verrannollisia, koska kulma δφ se on yleistä:

Voi palvella sinua: mikä on polarisoitua valoa?

 

Jakaminen ΔT: n välillä:

 Koska nopeuden määritelmällä on v = ΔL/ ΔT. Mutta ΔV// Δt Juuri se on centripetaalisen kiihtyvyyden suuruus, mitä etsitään. Tällä tavalla saavutetaan alussa kuvattu lauseke:

-lla_c= v²/r

Liikuntaa

Hiukkas liikkuu 2: n ympyrässä.70 m radio. Tietyssä vaiheessa sen kiihtyvyys on 1.05 m/s² Suuntaan, joka tekee 32 kulman.0º liikuntaosastolla. Laske nopeus:

a) tuolloin

b) 2.00 sekuntia myöhemmin, olettaen jatkuvan tangentiaalisen kiihtyvyyden.

Vastaus

Se on monipuolinen pyöreä liike, koska lausunto osoittaa, että kiihtyvyydellä on annettu kulma liikkeen suunnan kanssa, joka ei ole tai 0º (se ei voisi olla pyöreä liike) tai 90º (se olisi tasainen pyöreä liike).

Siksi kaksi komponenttia - säteittäistä ja tangentiaalista - rinnakkain. Merkitään nimellä_c jo_t ja esiintyy seuraavassa kuvassa. Vihreä vektori on nettokiihdytysvektori tai yksinkertaisesti kiihtyvyys -lla.

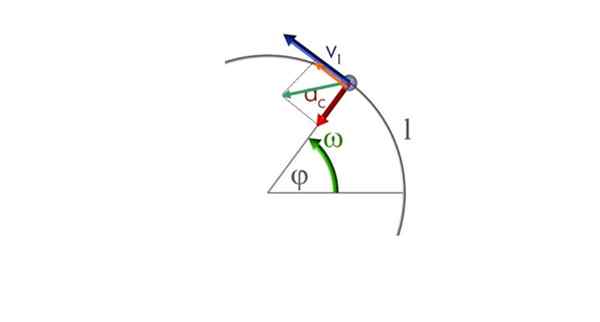Hiukkas liikkuu pyöreällä radalla antihorarisen mielessä ja monipuolinen pyöreä liike. Lähde: Commons.Wikimedia.org

a) kiihtyvyyskomponenttien laskeminen

-lla_c = a.cos θ = 1.05 m/s² . cos 32.0º = 0.89 m/s² (punaisessa)

-lla_t = a.synti θ = 1.05 m/s² . SEN 32.0º = 0.57 m/s² (oranssina)

Liikkuvan nopeuden laskenta

Koska a_c = v²/r, niin:
b) 2 sekuntia myöhemmin nopeus v kasvatetaan kiihtyvyyden tangentiaalisen komponentin ansiosta

V = V_jompikumpi +-lla_t. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Viitteet

1. Giancoli, D. Fysiikka. 2006. Periaatteet hakemuksissa. Kuudes painos. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides painos.Pearson.106 - 108.