Painovoiman kiihtyvyys mikä se on, miten se mitataan ja harjoittaa

Se Painovoima o Gravitaatioki. Toisin sanoen voima, jota tämä käyttää mihin tahansa esineeseen, massayksikköä kohti.

Se on merkitty jo tutulla kirjaimella G ja sen likimääräinen arvo maan pinnan läheisyydessä on 9.8 m/s². Tämä arvo voi kokea pieniä variaatioita maantieteellisellä leveysasteella ja myös korkeudella merenpinnan suhteen.

Astronautti avaruuspaseossa maan pinnalla. Lähde: Pixabay

Painovoiman kiihtyvyydellä on mainitun suuruuden lisäksi suunta ja merkitys. Itse asiassa se on suunnattu pystysuoraan kohti maan keskustaa.

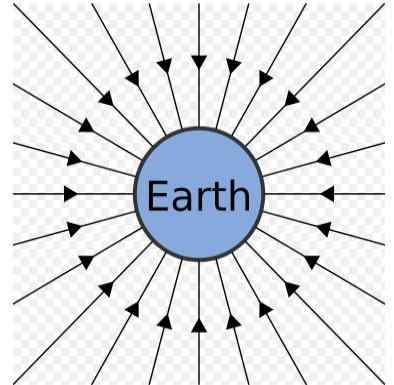Maapallon gravitaatiokenttä. Lähde: Lähde: Sjlegg [julkinen verkkotunnus]

Maan painovoimakenttä voidaan esitellä keskukseen osoittavien säteittäisten viivojen sarjana, kuten edellisessä kuvassa voidaan nähdä.

[TOC]

Mikä on painovoiman kiihtyvyys?

Painovoiman kiihtyvyyden arvo maapallossa tai millä tahansa muulla planeetalla vastaa sen tuottaman gravitaatiokentän voimakkuutta, mikä ei riipu sen ympärillä olevista esineistä, vaan vain omasta massastaan ​​ja sädeistään.

Usein painovoiman kiihtyvyys määritellään usein kiihtyvyydeksi, jonka kaikki esineet ovat kokeneet maan pinnan läheisyydessä olevassa vapaassa pudotuksessa.

Käytännössä näin melkein aina tapahtuu, kuten näemme seuraavissa osissa, joissa käytetään Newtonin yleistä gravitaatiolakia.

Sanotaan. Tunnettaessa omenan iskun päähänsä, hän tiesi heti, että omenan putoamisen voiman tekemä voima on sama, mikä saa kuun kierroksen maan ympärillä.

Yleinen gravitaatiolaki

Tietty tai ei omenalegenda, Newton tajusi, että kaikkien kahden esineen välillä, esimerkiksi maapallon ja kuun, maan ja maan ja omenan välillä, oli riippuvainen näiden massoista:

Missä m₁ Se voi olla maan massa ja m_2, Kuun tai omenan massa. Runkojen keskuudessa on suurempi massa, suurempi vetovoima. Mutta enemmän etäisyydellä, vähemmän voimaa, koska tämän on oltava käänteisesti verrannollinen etäisyyden neliöön r - Se erottaa ne:

Voi palvella sinua: Joustavat iskut: ulottuvuudessa, erityistapauksissa, harjoituksissa

Tämä on totta riippumatta siitä, kuinka suuret tai pienet ovat kyseisiä massoja. Yhdistämällä nämä tosiasiat painovoima pysyisi tällä tavalla:

Tämän empiirisen lain valmiuden saamiseksi tarvitaan jatkuvaa suhteellisuutta. Newton laski vakion G, joten kaava kuvaa kaikilla tarkkuuksilla taivaankappaleiden liikkeitä aurinkokunnan mittakaavassa ja sen ulkopuolella:

Missä g = 6.67 x 10^-yksitoista N.m²/kg²

Gravitaatiovoiman ominaisuudet

Gravitaatiovoima on aina houkutteleva; toisin sanoen kaksi ruumista, joihin se vaikuttaa, houkuttelevat toisiaan. Päinvastoin ei ole mahdollista, koska taivaankappaleiden kiertoradat ovat suljettuja tai avoimia (esimerkiksi komeetat) ja torjuntavoima ei voi koskaan tuottaa suljettua kiertorata. Sitten massot houkuttelevat aina mitä tapahtuu.

Melko hyvä lähestymistapa maan todelliseen muotoon (M₁) Ja kuu tai omena (m₂) on olettaa, että heillä on pallomainen muoto. Seuraava luku on tämän ilmiön esitys.

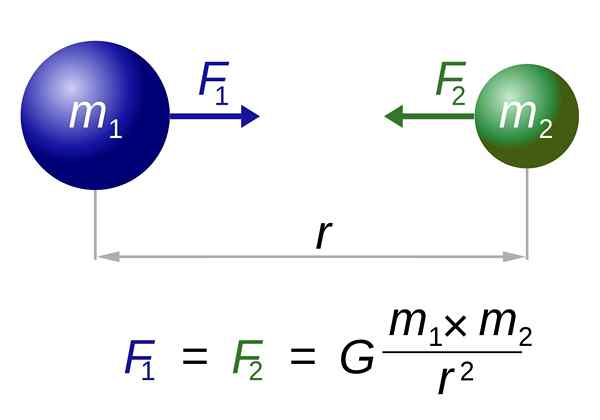Newtonin yleinen gravitaatiolaki. Lähde: I, Dennis Nilsson [CC 3: lla.0 (https: // creativecommons.Org/lisenssit/by/3.0)]

Tässä ovat molemmat voimat, joita kohdistetaan m₁ Noin m₂, Kuten se, joka harjoittaa m₂ Noin m₁, molemmat yhtä suuret ja ohjataan keskuksiin liittyvää linjaa pitkin. Niitä ei peruuteta, koska niitä sovelletaan eri esineisiin.

Kaikissa seuraavissa osissa oletetaan, että esineet ovat homogeenisia ja pallomaisia, joten sen painopiste vastaa sen geometristä keskustaa. Kaikki keskittyneen massan voidaan olettaa juuri siellä.

Kuinka painovoima mitataan eri planeetoilla?

Painovoima voidaan mitata liemetrillä, laitteella, joka palvelee vakavuutta mitattuna geofysikaalissa gravimetrisissa tutkimuksissa. Ne ovat tällä hetkellä paljon hienostuneempia kuin alkuperäiset, mutta alussa he perustuivat heiluun.

Heiluri koostuu ohuesta, kevyestä ja keksimättömästä köydestä, jonka pituus on L -. Yksi sen päistä on kiinnitetty yhteen tukeen ja toinen roikkuu massa m.

Kun järjestelmä on tasapainossa, taikina roikkuu pystysuunnassa, mutta kun se erotetaan siitä, se alkaa värähtelyä kääntymisliikkeen ajamalla. Gravity vastaa siitä. Kaikesta seuraavasta on pätevä olettaa, että painovoima on ainoa voima, joka toimii heiluun.

Voi palvella sinua: Aerostaattinen ilmapallo: Historia, ominaisuudet, osat, miten se toimii

Pienten värähtelyjen heilurin heilunjakso annetaan seuraavalla yhtälöllä:

Voima T ei riipu massasta, vaan L: n ja G: n arvosta. Neliö molemmat yhtälön jäsenet ovat:

Suhde välillä T² ja Lens Se on lineaarinen: muodon viiva y = a.x, missä arvo -lla, Viivan kaltevuus on tarkasti (4π²/g).

Koe määrittää g

Materiaalit

- 1 metallipallosiitti.

- Köysi, joka on useita eripituisia, vähintään 5.

- Mittanauha.

- Kuljettaja.

- Kronometri.

- Tuki heilurin asettamiseen.

- Laitetaulukko- tai tietokoneohjelma.

Menettely

1. Valitse yksi jousista ja koota heiluri. Mittaa köyden pituus + pallon säde. Tämä on pituus L.
2. Poista heiluri tasapainoasennosta noin 5 astetta (tunnusta se kuljettajan kanssa) ja jätä se värähtelemään.
3. Käynnistä samanaikaisesti sekuntikello ja mittaa 10 värähtelyn aika. Kirjoita tulos muistiin.
4. Toista aikaisempi menettely muille pituuksille.
5. Löydä heiluri, joka vie heilurin värähtelyn suorittamiseen (jokaisen aiemman tuloksen jakaminen 10: llä).
6. Neliö jokainen saatu arvo, hankkimalla T²
7. Millimetrin paperissa kuvaavat jokainen T -arvo² Pystysuoralla akselilla, vastaavaa L: n arvoa vaaka -akselilla. Ole yhdenmukainen yksiköiden kanssa ja älä unohda ottaa huomioon käytettyjen instrumenttien arvostusta koskevaa virhettä: metrinen nauha ja sekuntikello.
8. Piirrä paras viiva, joka sopii graafisiin pisteisiin.
9. Etsi kaltevuus m tästä linjasta käyttämällä kahta siihen kuuluvaa pistettä (ei välttämättä kokeellisia pisteitä). Lisää kokeellinen virhe.
10. Yllä olevat vaiheet voidaan suorittaa laskentataulukon kanssa ja vaihtoehto rakentaa ja säätää suoraa linjaa.
11. Kaltevuuden arvosta -lla Tyhjennä arvo g Heidän kokeellisen epävarmuutensa kanssa.

Vakioarvo g Maan päällä, kuuhun ja Marsiin

Painovoiman vakioarvo maan päällä on: 9.81 m/s², 45: llä pohjoisesta leveysasteesta ja merenpinnasta. Koska maa ei ole täydellinen pallo, arvot g Ne vaihtelevat hiukan, koska ne ovat suurempia Ecuadorin pylväissä ja alaikäisissä.

Ne, jotka haluavat tietää sijainnin arvon, voivat löytää sen päivitetyn Saksan PTB: n metrologiainstituutin verkkosivustolla (Physikalisch-Technische Bundesanstalt), osassa Painovoimajärjestelmä (LIITU).

Se voi palvella sinua: Ohjaajavektori: Suora yhtälö, ratkaistut harjoitukset

Kuun painovoima

Kuun painovoimakenttä on määritetty analysoimalla satelliittia kiertävien avaruuskoettimien radiosignaaleja. Sen arvo kuun pinnalla on 1.62 m/s²

Marsin vakavuus

Arvo g_P Planeetalle se riippuu massa M ja sädistään seuraavasti:

Siksi:

Planeetta Marsille seuraavat tiedot ovat käytettävissä:

M = 6 4185 x 10²³ kg

R = 3390 km

G = 6.67 x 10^-yksitoista N.m²/kg²

Näiden tietojen avulla tiedämme, että Marsin vakavuus on 3.71 m/s². Sama yhtälöä voidaan luonnollisesti soveltaa kuutietoihin tai mihin tahansa muuhun planeetaan ja arvioida siten sen vakavuuden arvo.

Ratkaistu harjoitus: putoaa omenaa

Oletetaan, että sekä maapallolla että omenalla on pallomainen muoto. Maan massa on M = 5,98 x 10²⁴ Kg ja sen säde on r = 6,37 x 10⁶  m. Omenan massa on M = 0.10 kg. Oletetaan, että muuta voimaa ei ole paitsi painovoima. Newtonin yleismaailmallisesta gravitaatiolaista:

a) omenaan kohdistettu painovoimavoima.

b) Newtonin toisen lain mukaan Applen kokenut kiihtyvyys vapauttaessaan sitä tietystä korkeudesta.

Ratkaisu

a) Applella (oletettu pallomainen, aivan kuten maa) on hyvin pieni säde verrattuna maanpäälliseen säteeseen ja se on upotettu sen painovoimakentään. Seuraava luku ei ole selvästi, mutta gravitaatiokentän kaavio g, Ja rasitus F Maan harjoittama omena:

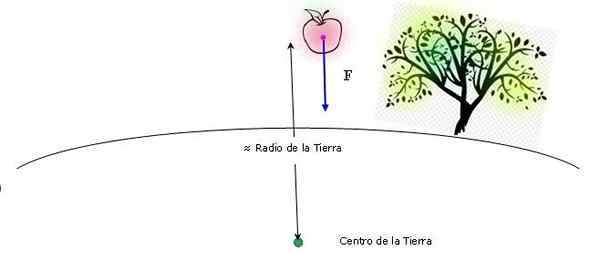Kaavio, joka osoittaa omenan kaatumisen maan läheisyydessä. Sekä omenan koko että syksyn korkeus ovat halveksittavia. Lähde: Itse tehty.

Kun levitetään Newtonin yleistä gravitaatiolakia, keskuksien välistä etäisyyttä voidaan pitää suunnilleen samana arvona kuin maan säde (korkeus, josta omena putoaa, on myös merkityksetön verrattuna maanpäälliseen säteeseen). Siksi:

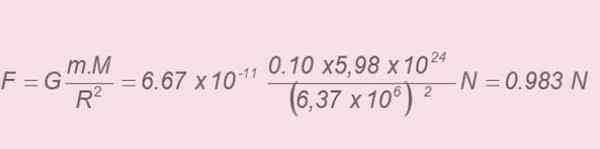
b) Newtonin toisen lain mukaan omenaan kohdistuvan voiman suuruus on:

F = ma = mg

Kenen arvo on 0.983 n, edellisen laskelman mukaan. Saadaan molemmat arvot ja sitten kiihtyvyyden suuruuden tyhjentäminen:

Mg = 0.983 n

G = 0.983 N/0.10 kg = 9.83 m/s²

Tämä on erittäin hyvä lähestymistapa painovoiman vakioarvoon.

Viitteet

1. Giancoli, D. (2006). Fysiikka: sovellusten periaatteet. Kuudes painos. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Käsitteellinen fysiikka. Viides painos. Pearson. 91 - 94.
3. Rex, a. (2011). Fysiikan perusteet. Pearson. 213-221.