Neliön ominaisuudet

Tavallinen neliö. Lisenssillä

Pää Neliön ominaisuus Se on tosiasia, että se muodostaa neljä osapuolta, joilla on täsmälleen samat toimenpiteet. Nämä puolet on järjestetty siten, että ne muodostavat neljä suoraa kulmaa (90 °).

Hän neliö Se on perusgeometrinen luku, tasaisen geometrian tutkimuksen kohde, koska se on kahden dimensioinen hahmo (joka on leveä ja pitkä, mutta puuttuu syvyys).

Neliöt ovat monikulmioita. Konkreettisemmalla tavalla ne ovat monikulmioita (a) neljännesten neljän puolen, (b) tasa -arvoiset puolet, jotka mittaavat saman ja (c) equiángulosin, joilla on kulmat, joilla on sama amplitudi, jolla on sama amplitudi.

Nämä neliön kaksi viimeistä ominaisuutta (tasapainon ja etäisyyden) voidaan tiivistää yhdellä sanalla: säännöllinen. Tämä tarkoittaa, että neliöt ovat säännöllisiä kvadrilateraalisia monikulmioita.

Kuten muutkin geometriset luvut, neliöllä on pinta -ala. Tämä voidaan laskea kertomalla yksi sen sivuista itsessään. Esimerkiksi, jos meillä on neliö, joka mittaa 4 mm, sen pinta -ala on 16 mm².

Neliöominaisuudet

1. Sivujen lukumäärä ja ulottuvuus

Neliöt koostuvat neljästä sivusta, jotka mittaavat saman. Lisäksi neliöt ovat kahden ulottuvuuden lukuja, mikä tarkoittaa, että niillä on vain kaksi ulottuvuutta: leveä ja korkea.

2. Monikulmio

Neliöt ovat monikulmioita. Tämä tarkoittaa, että neliöt ovat geometrisiä lukuja, jotka on rajattu suljetulla viivalla, joka muodostuu peräkkäisillä linjasegmenteillä (suljettu monikulmainen viiva).

Erityisesti se on nelinkertainen monikulmio, koska sillä on neljä puolta.

3. Tasasivuinen monikulmio

Sanotaan, että monikulmio on tasa -arvoinen, kun kaikilla sen sivuilla on sama mitta. Tämä tarkoittaa, että jos neliön toinen puoli mittaa 2 metriä, kaikki puolet mittaavat 2 metriä.

Se voi palvella sinua: mitä tapahtuu, jos maa olisi lähempänä aurinkoa?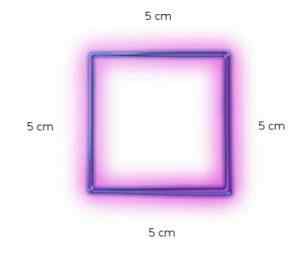

4. Evengle Polygon

Sanotaan.

Kaikki neliöt koostuvat neljästä suorasta kulmasta (ts. 90 ° kulmasta) riippumatta.

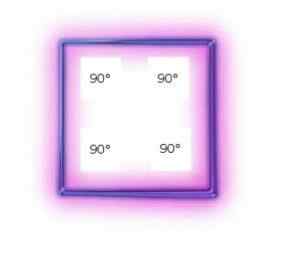
Kaikki neliöt ovat tasa -arvoisia, koska niiden kulmilla on sama amplitudi. Eli 90 °.

5. Tavallinen monikulmoni

Kun monikulmio on tasa -arvoinen ja samalla tasa -arvoinen, katsotaan, että tämä on tavallinen monikulmio.

Koska neliöllä on sivut, jotka mittaavat samat ja saman amplitudin kulmat, voidaan sanoa, että tämä on tavallinen monikulmio.

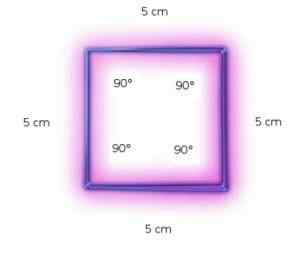
Neliöissä on yhtä suuret mittaiset ja saman amplitudin kulmat, joten ne ovat säännöllisiä monikulmioita.

6. Neliön pinta -ala

Neliön pinta -ala on yhtä suuri kuin toisella puolella oleva tuote. Koska molemmilla puolilla on täsmälleen sama mitta, kaavaa voidaan yksinkertaistaa sanomalla, että tämän monikulmion alue on yhtä suuri kuin sen sivuista, eli (sivu)².

Joitakin esimerkkejä neliön pinta -alan laskennasta ovat:

- Neliö, jonka sivut ovat 2 m: 2 m x 2 m = 4 m²

- Neliöt, joiden sivut ovat 52 cm: 52 cm x 52 cm = 2.704 cm²

- Neliö 10 mm: n sivuilla: 10 mm x 10 mm = 100 mm²

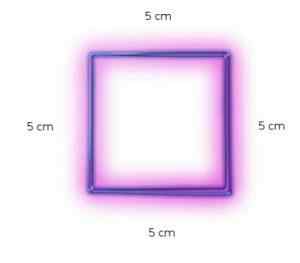
Kuvassa esitetyllä neliöllä on 5 cm: n sivut.

Alueesi on 5 cm x 5 cm tuote tai mikä on sama (5 cm)²

Voi palvella sinua: Hydrologia: Mikä on, historia, mitä tutkimuksia

Tässä tapauksessa neliön neliö on 25 cm²

7. Neliöt ovat rinnakkaisia

Rinnakkaisgrammit ovat eräänlainen kvadrilateraali, jolla on kaksi paria rinnakkaisia ​​sivuja. Tämä tarkoittaa, että pari puolta kohtaa toisiaan, kun taas sama tapahtuu toisen vääntömomentin kanssa.

Samanaikaisia ​​rinnakkaisia.

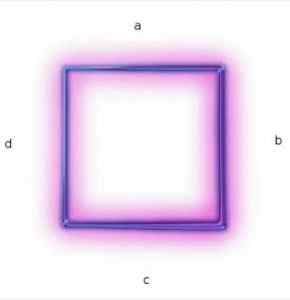
Neliöt ovat yhdensuuntaisia ​​ohjelmia, koska niillä on kaksi paria sivua, jotka ovat yhdensuuntaisia.

Sivut (a) ja (c) ovat yhdensuuntaiset.

Sivut (b) ja (d) ovat yhdensuuntaiset.

8. Vastakkaiset kulmat ovat yhdenmukaisia ​​ja peräkkäisiä täydentäviä

Että kaksi kulmaa ovat yhdenmukaisia ​​tarkoittaa, että heillä on sama amplitudi. Tässä mielessä, koska neliöllä on kaikki saman amplitudin kulmat, voidaan sanoa, että vastakkaiset kulmat ovat yhdenmukaisia.

Puolestaan ​​se, että kaksi peräkkäistä kulmaa on täydentävä, tarkoittaa, että näiden kahden summa on yhtä suuri kuin tasainen kulma (se, jonka amplitudi on 180 °)).

Neliön kulmat ovat suorat kulmat (90 °), joten sen summa 180 °.

9. Ne on rakennettu kehästä

Neliön rakentamiseksi piirretään kehä. Myöhemmin tähän kehälle piirretään kaksi halkaisijaa. Näiden halkaisijoiden on oltava kohtisuorassa, muodostaen ristin.

Kun halkaisijat on piirretty, meillä on neljä pistettä, joissa linjasegmentit leikkaavat kehän. Jos nämä neljä pistettä yhdistetään, neliö otetaan.

10. Diagonaalit leikataan niiden keskipisteessä

Diagonaalit ovat suoria viivoja, jotka on piirretty kulmasta toiseen, joka on vastapäätä. Neliöön voidaan piirtää kaksi diagonaalia. Nämä diagonaalit ylittävät neliön keskipisteessä.

Voi palvella sinua: Bibliografinen tutkimus: Määritelmä, tyypit, tekniikat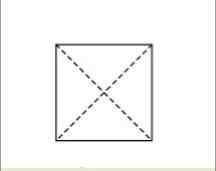

Kuvassa katkoviivat edustavat diagonaaleja. Kuten voidaan nähdä, nämä viivat ylittävät tarkalleen neliön keskellä.

Viitteet

1. Neliö ja sen ominaisuudet. Toipunut Mathonpenrefistä.com
2. Rhombusien, suorakaiteenkertojen ja neliöiden ominaisuudet. Nukkeet toipuivat.com