Radiaalinen kuorma miten lasketaan, ratkaistu harjoitukset

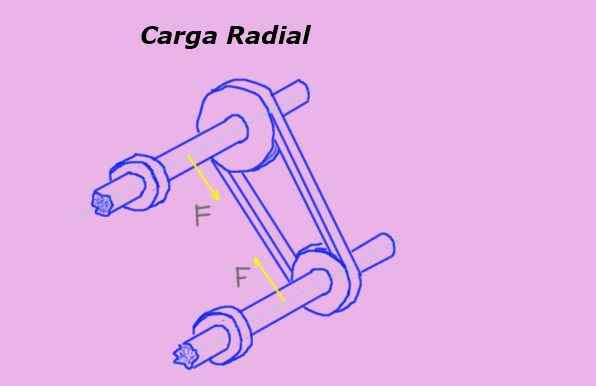
Se Radiaalikuorma Se on voima, jota käytetään kohtisuorassa esineen symmetrian akseliin ja jonka toimintalinja kulkee tämän akselin läpi. Esimerkiksi hihnapyörän hihna asettaa säteittäisen kuormituksen saman akselin laakerille tai laakerille.

Kuviossa 1 keltaiset nuolet edustavat säteittäisiä voimia akseleilla hihnapyörien läpi kulkevan hihnan jännityksen vuoksi.

Kuvio 1. Säteittäinen kuorma hihnapyörällä. Lähde: Itse tehty.

Radiaalikuorman mittayksikkö kansainvälisessä järjestelmässä tai jos se on Newton (n). Mutta muita voimayksiköitä käytetään myös sen mittaamiseen, kuten kilogrammi (KG-F) ja punnan lujuus (LB-F).

[TOC]

Kuinka se lasketaan? 

Radiaalikuorman arvon laskemiseksi rakenteen elementeissä on noudatettava seuraavia vaiheita:

- Tee voimien kaavio jokaisesta elementistä.

- Soveltaa yhtälöitä, jotka takaavat translaatiotasapainon; eli kaikkien voimien summa on tyhjä.

- Harkitse vääntömomenttien yhtälöä niin, että kiertotasapaino täyttyy. Tässä tapauksessa kaikkien vääntömomenttien summan on oltava tyhjä.

- Laske voimat tunnistamaan säteittäiset kuormat, jotka toimivat kussakin elementissä.

Ratkaisut

-Harjoitus 1

Seuraava kuva näyttää hihnapyörän, jonka kautta kireä hihnapyörä kulkee jännityksellä t. Hihnapyörä on asennettu akselille, joka lepää kahdessa chumacerassa. Yhden heistä keskusta on etäisyydellä L₁ hihnapyörän keskustasta. Toisessa päässä on toinen chumacera, etäisyydellä L₂.

Voi palvella sinua: Highoskooppisuus: konsepti, hygroskooppiset aineet, esimerkit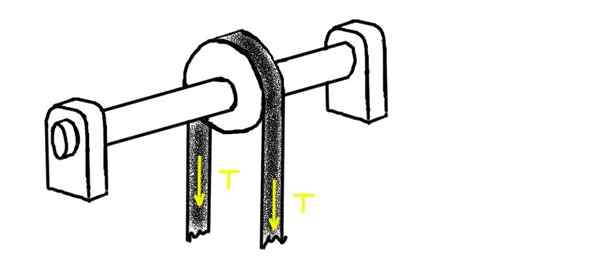Kuva 2. Hihnapyörä, jonka läpi kireä hihna kulkee. Lähde: Itse tehty.

Määritä säteittäinen kuormitus jokaisessa chumacerassa olettaen, että akselin ja hihnapyörän paino ovat melko alhaisemmat kuin käytetty jännite.

Ota arvona 100 kg-F-hihnajännitteelle ja etäisyyksille l₁= 1 m ja l₂= 2 m.

Ratkaisu

Ensinnäkin tehdään kaavio akselilla toimivista voimista.

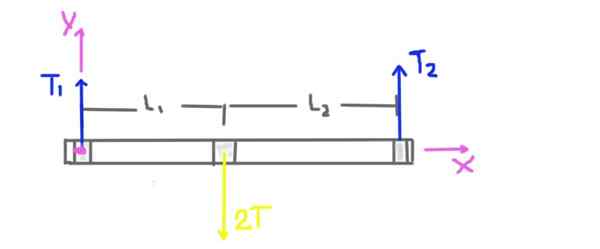Kuva 3. Harjoittelujoukot Kaavio 1.

Hihnapyörän jännite on t, mutta hihnapyörän asennon akselin säteittäinen kuormitus on 2T. Akselin ja hihnapyörän painoa ei oteta huomioon, koska ongelmalause kertoo meille, että se on paljon pienempi kuin hihnan levitetty jännite.

Tukituen säteittäinen reaktio johtuu säteittäisistä voimista tai kuormista T1 ja T2. Kaaviossa on myös osoitettu hihnapyörän keskuksen tukien etäisyydet L1 ja L2.

Koordinaattijärjestelmä on myös esitetty. Akselin vääntömomentti tai kokonaismomentti lasketaan keskuksena koordinaattijärjestelmän alkuperä ja se on positiivinen Z -suunnassa.

Tasapainoolosuhteet

Tasapainoolosuhteet on nyt vakiintunut: saman nollan summa ja vääntömomenttien summa nolla.

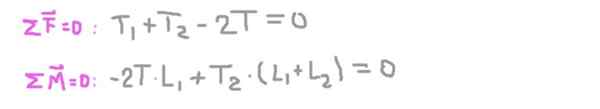
Toisesta yhtälöstä akselin säteittäinen reaktio tuella 2 (t₂), korvaaminen ensimmäisessä ja puhdistamalla radiaalireaktio akselilla tuen 1 (t₁-A.

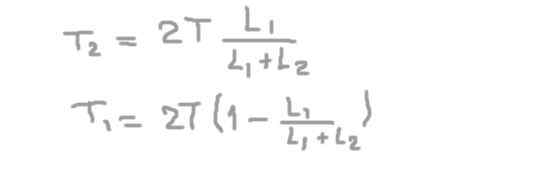Jos korvaamme numeeriset tiedot, saamme, että tuen asennon säteittäinen kuormitus tai voima 1 on:

T₁= (2/3) t = 66,6 kg-f

Se voi palvella sinua: Kalibrointikäyrä: Mihin se on, miten se tehdään, esimerkkejä

Ja akselin säteittäinen kuormitus tuki 2 on:

T₂= (4/3) t = 133,3 kg-F.

Harjoitus 2

Seuraava kuva näyttää järjestelmän, joka koostuu kolmesta hihnapyörästä A, B, C Kaikki radio r. Hihnapyörät on kytketty hihnalla, jolla on T -jännite.

Akselit A, B, C Passvoi voidelut laakerit. Akselien A ja B keskuksen välinen ero on 4 kertaa säde r. Samoin erotus akselien B ja C välillä on myös 4R.

Määritä säteittäinen kuorma hihnapyörien A ja B akseleilla olettaen, että hihnan jännitys on 600N.

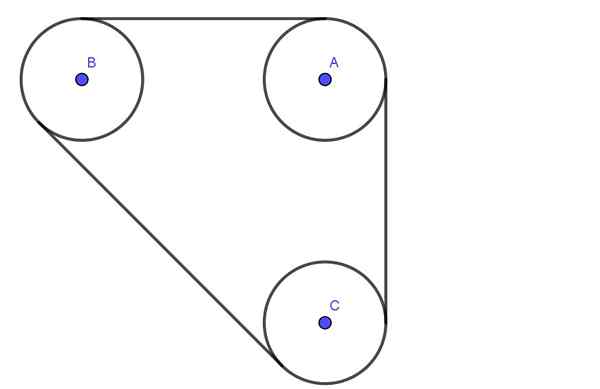Kuva 4. Hihnapyöräjärjestelmä. Harjoitus 2. (Oma yksityiskohta)

Ratkaisu

Se alkaa piirtämällä kaavio hihnapyörällä toimivista voimista A ja B. Ensimmäisessä sinulla on molemmat T -jännitteet₁ ja T₂, samoin kuin voima f_-Lla Että laakeri käyttää hihnapyörän akselia.

Samoin hihnapyörällä b sinulla on jännitteitä T₃ , T₄ ja voima f_{B -} että laakeri käyttää saman akselin. Hihnapyörän a -akselin säteittäinen kuorma on voima f_-Lla ja säteittäinen kuorma B: ssä on voima f_{B -}.

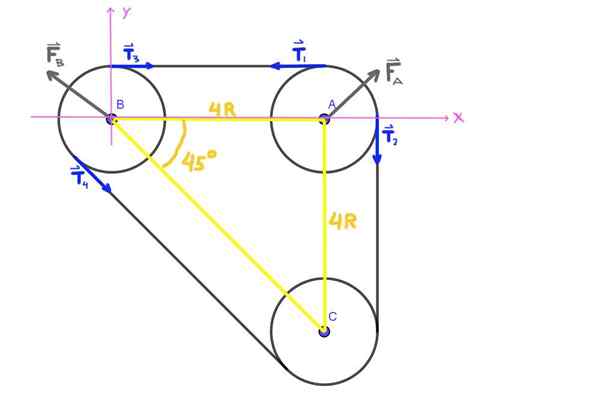Kuva 5. Joukkojen kaavio, harjoitus 2. (Oma yksityiskohta)

Kun akselit a, b, c muodostavat isorektanglikolmion, ABC -kulma on 45 °.

Kaikki jännitteet t₁ , T₂ , T₃ , T₄ Kuvassa on sama moduuli t, joka on hihnan jännite.

Hihnapyörän tasapainotus a

Nyt kirjoitamme hihnapyörän tasapainoolosuhteet, joihin se ei ole mitään muuta kuin kaikkien hihnapyörällä toimivien voimien summa a täytyy olla tyhjä.

Komponenttien x ja y erottaminen voimista ja lisäämällä (vektorisesti) seuraavat skalaariyhtälöparit saadaan:

Voi palvella sinua: Titan (satelliitti)

F_-LlaX - T = 0; F_-LlaJA - T = 0

Nämä yhtälöt johtavat seuraavaan tasa -arvoon: f_Kirves = F_{VAI NIIN} = T.

Siksi säteittäisellä kuormituksella on annettu suuruusluokka:

F_-Lla = (T² + t²)^1/2 = 2^1/2∙ T = 1,41 ∙ T = 848,5 N. 45 ° suunta. 

Hihnapyörän tasapainotus

Samoin kirjoitamme hihnapyörän tasapainon olosuhteet B. Komponentille x sinulla on: f_{B -X} + T + t ∙ cos45 ° = 0

Ja komponentille y: f_{B -JA} + T ∙ sen45 ° = 0

Täten:

F_Bx = - t (1+2^-1/2) ja f_Ohella = -T ∙ 2^-1/2

Eli hihnapyörän säteittäisen kuorman suuruus on:

F_{B -} = ((1+2^-1/2) ² + 2^-1-A^1/2∙ T = 1,85 ∙ T = 1108,66 N ja sen osoite on 135 °.

Viitteet

1. Olut F, Johnston E, DeWolf J, Mazurek, D. Materiaalimekaniikka. Viides painos. 2010. MC Graw Hill. 1-130.
2. Gere J, Goodno, B. Materiaalimekaniikka. Kahdeksas painos. Cengage -oppiminen. 4-220.
3. Giancoli, D. 2006. Fysiikka: sovellusten periaatteet. 6^Tth Ed. Prentice Hall. 238-242.
4. Hibbeler R. Materiaalimekaniikka. Kahdeksas painos. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 87-98.