Moody -kaavioyhtälöt, mihin se on, sovellukset

Hän Mielialakaavio Se koostuu logaritmiselle paperille piirrettyjen käyrien sarjasta, joita käytetään laskemaan turbulentin nesteen virtauksen kitkakerroin pyöreän kanavan läpi.

Kitkakertoimella F Kitkaenergian menetys arvioidaan, tärkeä arvo määrittääkseen nesteet, kuten vesi, bensiini, raaka.

Putket teollisuusasteella. Lähde: Pixabay.

Nesteen virtauksen energian tunteminen on välttämätöntä ja putken seinät.

[TOC]

Yhtälöt liikkeenesteen energialle

Putken kahden osan välillä, merkittynä 1 ja 2, Seuraava tasapaino on mahdollista selvittää, mikä on Bernoulli -yhtälön laajennus: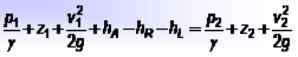Missä:

- p₁ ja p₂ ovat paineita kussakin vaiheessa,

- z -z₁ ja z -z₂ ovat korkeuksia vertailupisteen suhteen,

- v₁ ja v₂ ovat vastaavat nesteen nopeudet,

- h_-Lla Se on pumppujen lisäämä energia, h_{R -} Se on laitteen kaltaisen laitteen energia h_Lens Se kattaa nesteenergiahäviöt, jotka johtuvat tämän ja putkien seinien välisestä kitkasta, samoin kuin muut pienet tappiot.

Arvo h_Lens Se lasketaan käyttämällä Darcy-Weisbach-yhtälöä:

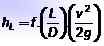
Missä Lens Se on putken pituus, D -d Se on sen sisähalkaisija, v Se on nesteen nopeus ja g Se on painovoiman kiihtyvyyden arvo. Mitat h_Lens Ne ovat pitkiä, ja yleensä yksiköt, joissa se on edustettuna, ovat mittarit tai jalat.

-Kitkakerroin ja Reynolds -numero

Laskea F Koetiedoista saatuja empiirisiä yhtälöitä voidaan käyttää. On välttämätöntä erottaa, onko kyse laminaarisessa järjestelmässä tai turbulenssissa järjestelmässä nestettä. Laminaariryhmälle F Se arvioidaan helposti:

F = 64/n_{R -}

Missä N_{R -} Se on Reynolds -luku, jonka arvo riippuu tilasta, jossa neste sijaitsee. Kriteerit ovat:

Laminaarivirta: n_{R -} < 2000 el flujo es laminar; Flujo turbulento N_{R -} > 4000; Siirtymäjärjestelmä: 2000 < N_{R -} < 4000

Reynoldsin numero (mitatton) puolestaan ​​riippuu nesteenopeudesta v, Putkilinjan sisähalkaisija D -d ja kinemaattinen viskositeetti n nesteestä, jonka arvo saadaan pöydillä:

Voi palvella sinua: tasaisesti kiihdytetty välitöntä liikettä: Ominaisuudet, kaavat

N_{R -} = v.D /n

Colebrook -yhtälö

Turbulenttia virtausta varten kuparin ja lasiputkien hyväksytty yhtälö on Cyril Colebrookin (1910-1997) virtaus, mutta sillä on haittaa, että se on haittaa F Se ei ole selkeä:

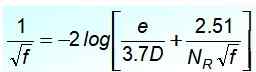
Tässä yhtälössä osuus E/D Se on putken suhteellinen karheus ja N_{R -} Se on Reynolds -numero. Kun sitä tarkkailtaan huolellisesti, huomataan, että poistuminen ei ole helppoa F Tasa -arvon vasemmalla puolella, joten se ei ole kätevä välittömille laskelmille.

Colebrook itse ehdotti tätä lähestymistapaa, joka on selkeä, pätevä joidenkin rajoitusten kanssa:

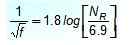
Mitä varten se on?

Moodyn kaavio on hyödyllinen kitkakertoimen löytämisessä F Sisältää Darcy -yhtälöön ottaen huomioon, että Colebrook -yhtälössä ei ole helppo ilmaista F suoraan muiden arvojen suhteen.

Sen käyttö yksinkertaistaa arvon saamista F, sisältämällä graafinen esitys F toiminnassa N_{R -} Suhteellisen karheuden eri arvoille logaritmisella asteikolla.

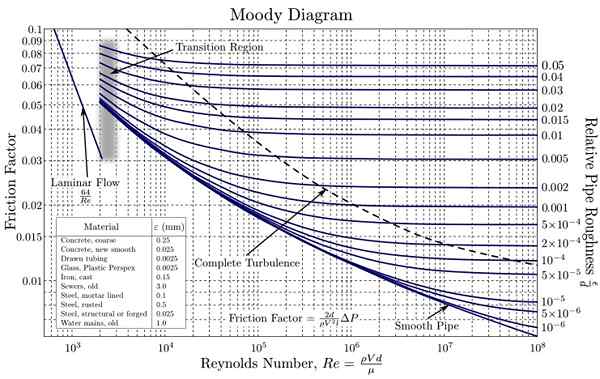Mielialakaavio. Lähde: https: // lataus.Wikimedia.org/wikipedia/commons/d/d9/moody_en.SVG

Nämä käyrät on luotu kokeellisista tiedoista, joissa on erilaisia ​​materiaaleja, joita käytetään yleisesti putkien valmistuksessa. Logaritmisen asteikon käyttö molemmille F mitä tahansa N_{R -} Se on välttämätöntä, koska ne kattavat erittäin laajan arvon. Tällä tavoin helpotetaan erilaisten suuruusluokkien arvojen piirtämistä.

Colebrook-yhtälön ensimmäisen kaavion saatiin insinööri Hunter Rouse (1906-1996) ja pian sen jälkeen sitä muutti Lewis F. Moody (1880-1953), jolla sitä käytetään tällä hetkellä.

Sitä käytetään sekä ympyrä- että ei -ympyräputkiin, se riittää korvaamaan näiden hydraulinen halkaisija.

Miten se tehdään ja miten sitä käytetään?

Kuten edellä selitettiin, tunnelmallinen kaavio on valmistettu lukuisista kokeellisista tiedoista, esitetty graafisesti. Tässä ovat vaiheet sen käyttämiseen:

- Laske Reynolds -luku N_{R -} Sen määrittämiseksi, onko virtaus laminaarinen vai turbulentti.

- Laske suhteellinen karheus yhtälöllä ja_{r -} = E/d, missä ja Se on materiaalin absoluuttinen karheus ja D on putken sisähalkaisija. Nämä arvot saadaan taulukolla.

- Nyt kun se on käytettävissä ja_{r -} ja N_{R -}, Projekti pystysuunnassa, kunnes saavutetaan käyrä, joka vastaa ja_{r -} saatu.

- Projekti vaakasuoraan ja vasemmalle lukemaan F.

Esimerkki visualisoi helposti, kuinka kaavio käytetään.

Voi palvella sinua: kalsiumfluori (CAF2): rakenne, ominaisuudet, käyttötarkoitukset

-Ratkaistu esimerkki 1

Määritä veden kitkakerroin lämpötilassa 160º F, joka virtaa nopeudella 22 jalkaa/s kanavassa, joka on valmistettu päällystetyistä takoraudasta ja sisähalkaisijasta 1 tuumaa.

Ratkaisu

Tarvittavat tiedot (löytyy taulukoista):

Vesikinemaattinen viskositeetti nopeudella 160 ºF: 4.38 x 10^-6 jalka²/s

Takaraudan ehdoton karheus ei katettu: 1.5 x 10 ^-4 jalat

Ensimmäinen askel

Reynolds -luku on laskettu, mutta ei ennen kuin se ohittaa 1 tuuman sisähalkaisijan jalkoissa:

1 tuuma = 0.0833 jalkaa

N_{R -} = (22 x 0.0833)/ 4.38 x 10^-6= 4.18 x 10 ⁵

Ennen kuin se on turbulentti virtaus, mukaan lukien, mielialainen kaavio mahdollistaa vastaavan kitkakerroksen saamisen, jolloin sinun tarvitsee käyttää Colleeroebook -yhtälöä.

Toinen askel

Sinun on löydettävä suhteellinen karheus:

ja_{r -} = 1.5 x 10 -4 / 0.0833 = 0.0018

Kolmas askel

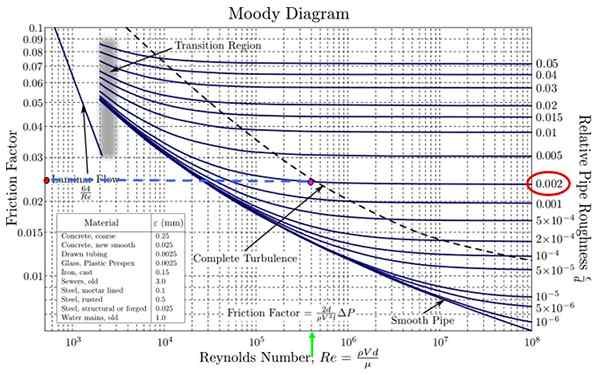
Toimitetussa Moody -kaaviossa se on välttämätöntä. Ei ole ketään, joka vastaa tarkalleen 0: ssa.0018 Mutta on yksi, joka lähestyy paljon, 0.002 (kuvan punainen soikea).

Samanaikaisesti vastaava Reynolds -numeroa etsitään vaaka -akselilla. Arvo, joka on samanlainen kuin 4.18 x 10 ⁵ on 4 x 10 ⁵ (Vihreä nuoli kuvassa). Molempien leikkaus on fuksiapiste.

Neljäs vaihe

Projekti vasemmalle vasemmalle pisteviivalle ja päästä oranssipisteeseen. Arvioi nyt F, Kun otetaan huomioon, että jakautumisilla ei ole samankokoista kuin se on logaritminen asteikko sekä vaakasuorassa että pystysuorassa akselissa.

Kuvassa toimitetulla mielialaisella kaaviolla ei ole hienoja vaakasuoria jakoja, joten arvo F in 0.024 (on välillä 0.02 ja 0.03 Mutta se ei ole puoli, mutta vähän vähemmän).

On online. Yksi niistä (katso viitteet) toimitettu arvo 0.023664639 kitkakerroin.

Sovellukset

Moody -kaaviota voidaan soveltaa kolmen tyyppisten ongelmien ratkaisemiseksi edellyttäen, että putken neste ja absoluuttinen karheus tunnetaan:

- Painehäviön laskeminen tai kahden pisteen välisten paineiden ero, toimitti putken pituuden, pituuden korkeusero, joka on otettava huomioon, nopeus ja putken sisäinen halkaisija.

Voi palvella sinua: Pendulaarinen liike

- Virtauksen määrittäminen, tunnettu putken pituus ja halkaisija sekä spesifinen painepisara.

- Putken halkaisijan arviointi, kun tiedossa olevien pisteiden pituus, virtaus ja paine pudotus.

Ensimmäisen tyypin ongelmat ratkaistaan ​​suoraan käyttämällä kaaviota, kun taas toisen ja kolmannen tyypin ongelmat vaativat laskennallisen paketin käyttöä. Esimerkiksi kolmannen tyyppisen tyypin, jos putken halkaisijaa ei tiedetä, Reynolds -lukua ei voida arvioida suoraan eikä suhteellista karheutta.

Yksi tapa ratkaista ne on ottaa alkuperäinen sisähalkaisija ja sieltä säätää arvoja peräkkäin ongelman määritetyn paineen pudotuksen saamiseksi.

-Ratkaistu esimerkki 2

Siinä on vettä lämpötilassa 160 ° F. Määritä kitkan ja pumppausvoiman aiheuttama paine -ero, joka tarvitaan virtauksen ylläpitämiseksi vaakasuuntaisen putken osuudessa L = 200 jalkaa pitkä.

Ratkaisu

Tarvittavat tiedot: Painovoiman kiihtyvyys on 32 jalkaa/s² ; Veden ominaispaino 160 ºF: n nopeudella on γ = 61.0 lb-voima/jalka³

Tämä on esimerkin putki ratkaistu 1, joten kitkakerroin on jo tiedossa F, jonka on arvioitu 0.0024. Tämä arvo viedään Darcy -yhtälöön kitkahäviöiden arvioimiseksi:

Tarvittava pumppausteho on:

W = v. -Lla. (p₁ - p₂-A

Missä a on putken poikkileikkaus: a = p. (D²/4) = P. (0.0833²/4) jalka² = 0.00545 jalka²

W = 22 jalkaa /s . 2659.6 lb-voima / jalka². 0 -.00545 jalka²= 318.9 lb-voima . jalat

Voima ilmaistaan ​​paremmin Wattsissa, jolle muuntamiskerroin vaaditaan:

1 watti = 0.737 lb-voima . jalat

Siksi virtauksen ylläpitämiseen tarvittava voima on w = 432.7 W

Viitteet

1. Cimbala, c. 2006. Nesteiden, perusteiden ja sovellusten mekaniikka. MC. Graw Hill. 335-342.
2. Franzini, J. 1999. Nesteen mekaniikka levittämällä on tekniikka. MC. Graw Hill.176-177.
3. LMNO -tekniikka. Moody kitkalaskinkerroin. Toipunut: lmnoeng.com.
4. Mott, r.  2006. Fluidimekaniikka. Neljäs. Painos. Pearson -koulutus. 240-242.
5. Suunnittelutyökalupakki. Mielialakaavio. Toipunut: EngineeringToolbox.com
6. Wikipedia. Tunnelmallinen kaavio. Toipunut: vuonna.Wikipedia.org