Joustavat iskut ulottuvuudessa, erityistapauksissa, harjoituksissa

Se joustavat iskut o Joustavat törmäykset koostuvat lyhyistä, mutta intensiivisistä vuorovaikutuksista esineiden välillä, joissa sekä liikkeen määrä että kineettinen energia säilytetään. Choques on luonteeltaan hyvin yleisiä tapahtumia: subatomisista hiukkasista galakseihin, biljardipallojen läpi ja iskuautoihin vetovoimapuistoissa, kaikki ovat esineitä, jotka kykenevät törmäämään.

Törmäyksen tai sokin aikana esineiden väliset vuorovaikutusvoimat ovat erittäin voimakkaita, paljon enemmän kuin ne, jotka voivat toimia ulkoisesti. Tällä tavalla voidaan vahvistaa, että törmäyksen aikana hiukkaset muodostavat eristetyn järjestelmän.

Biljardipallojen välisiä törmäyksiä voidaan pitää joustavina. Lähde: Pixabay.

Tässä tapauksessa on toteutettu, että:

Missä P Se on liikkeen vektorimäärää, jonka suuruus on MV (Nopeusmassa). Jos johdannainen P on tyhjä, se tarkoittaa sitä P se on vakio. Ja tämä tarkoittaa, että se ei vaihtele, että se säilyy. Siksi voimme vahvistaa sen:

P_jompikumpi = P_F

Liikkeen määrä P_jompikumpi Ennen törmäystä on sama kuin törmäyksen jälkeen. Tämä saavutetaan kaiken tyyppiselle törmäykselle, sekä joustavalle että joustamaton.

Nyt sinun on harkittava seuraavaa: törmäyksen aikana esineet kokevat tietyn muodonmuutoksen. Kun yhteentörmäys on joustava, esineet palauttavat nopeasti alkuperäisen muodonsa.

[TOC]

Kineettinen energian säilyttäminen

Normaalisti iskun aikana osa esineiden energiaa käytetään kuumuuteen, muodonmuutokseen, ääneen ja joskus jopa valon tuottamiseen. Joten järjestelmän kineettinen energia törmäyksen jälkeen on pienempi kuin alkuperäinen kineettinen energia.

Kun kineettinen energia k, se säilyy sitten:

K -k -_jompikumpi = K_F

Mikä tarkoittaa, että törmäyksen aikana toimivat voimat ovat konservatiivisia. Vaikka törmäys kestää, kineettinen energia muuttuu hetkeksi potentiaaliseksi energiaksi ja sitten se on taas kineettinen energia. Vastaavat kineettiset energiat vaihtelevat, mutta summa pysyy vakiona.

Täydellisesti joustavat törmäykset eivät ole usein, vaikka biljardipallot ovat melko hyvä lähestymistapa, samoin kuin törmäykset, jotka tapahtuvat ihanteellisten kaasumolekyylien välillä.

Joustavat iskut ulottuvuudessa

Tutkitaan kahden hiukkasen törmäys yhdessä ulottuvuudessa; Eli hiukkaset, jotka ovat vuorovaikutuksessa, liikkuvat esimerkiksi x -akselia pitkin. Oletetaan, että heillä on massat m₁ ja m₂. Kunkin alkuperäiset nopeudet ovat tai₁ ja tai₂ vastaavasti. Lopulliset nopeudet ovat v₁ ja v₂.

Voimme tehdä ilman vektorimerkintää, koska liike suoritetaan X-akselia pitkin, merkit (-) ja (+) osoittavat liikkeen merkityksen. Vasemmalla on negatiivinen ja positiiviseen oikeaan, valmistelukuntan mukaan.

Voi palvella sinua: Bravais Networks: Konsepti, ominaisuudet, esimerkit, harjoitukset

-Joustavien törmäysten kaavat

Liikkeen määrän

m₁tai₁ + m₂tai₂ = m₁v₁ + m₂v₂

Kineettisen energian kannalta

½ m₁tai²₁ + ½ m₂tai²₂ = ½ m₁v²₁ +  ½ m₂v²₂

Aina kun alkuperäiset massat ja nopeudet tunnetaan, on mahdollista ryhmitellä yhtälöt uudelleen lopullisten nopeuksien löytämiseksi.

Ongelmana on, että periaatteessa se on välttämätöntä. Ihanteellinen olisi löytää ilmaisuja, jotka eivät sisällä niitä.

Ensimmäinen on tehdä ilman ½ -tekijää ja järjestää molemmat yhtälöt siten, että negatiivinen merkki ilmestyy ja massat voivat olla tekijä:

m₁tai₁ - m₁v₁ = M₂v₂ - m₂tai₂

m₁tai²₁ - m₁v²₁  = +M₂v²₂ - m₂tai²₂

Ilmaistaan ​​tällä tavalla:

m₁(tai₁ - v₁ ) = m₂(V₂ - tai₂-A

m₁(tai²₁ - v²₁ ) = m₂ (V²₂ - tai²₂-A

Yksinkertaistaminen neliöiden poistamiseksi nopeuksista

Nyt sinun on käytettävä merkittävää tuotetta, se lisää sen eroa toisessa yhtälössä, joka saa lausekkeen, joka ei sisällä neliöitä, kuten alun perin haluttiin:

m₁(tai₁ - v₁ ) = m₂(V₂ - tai₂-A

m₁(tai₁ - v₁ ) (tai₁ + v₁ ) = m₂ (V₂ - tai₂) (v₂ + tai₂-A

Seuraava vaihe on korvata ensimmäinen yhtälö toisessa:

m₂(V₂ - tai₂) (tai₁ + v₁ ) = m₂ (V₂ - tai₂) (v₂ + tai₂-A

Ja kun termi toistetaan m₂(V₂ - tai₂-A Tasa -arvon molemmilla puolilla tämä termi peruutetaan ja on tällainen:

(tai₁ + v₁) = (V₂ + tai₂-A

Tai vielä parempi:

tai₁ - tai₂= v₂ -  v₁

Lopulliset nopeudet v₁ ja v₂ hiukkasista

Nyt on kaksi lineaarista yhtälöä, joiden kanssa on helpompi työskennellä. Sijoitamme ne uudelleen toisen alle:

m₁tai₁ + m₂tai₂ = m₁v₁ + m₂v₂

tai₁ - tai₂= v₂ -  v₁

Kertomalla toinen yhtälö m₁ Ja termin lisääminen termiin pysyy:

m₁tai₁ + m₂tai₂ = m₁v₁ + m₂v₂

m₁tai₁ - m₁tai₂= m₁v₂ - m₁ v₁

-

2 m₁tai₁ + (m₂ - m₁tai₂ = (m₂ + m₁) v₂

Ja on jo mahdollista puhdistaa v₂. Esimerkiksi:

Samanlainen hoito voidaan tehdä yhtälön löytämiseksi v₁. Lukija jätetään harjoitukseksi osoittaakseen, että:

Erityistapaukset joustavissa törmäyksissä

Nyt kun yhtälöitä on saatavana molempien hiukkasten lopullisille nopeuksille, on aika analysoida joitain erityisiä tilanteita.

Kaksi identtistä massaa

Sitten m₁ = m₂ = m ja:

v₁ = u₂

v₂ = u₁

Hiukkaset vain vaihtavat nopeutensa törmäyksen jälkeen.

Kaksi identtistä massaa, joista toinen oli alun perin levossa

Uudelleen  m₁ = m₂ = m ja olettaen, että tai₁ = 0:

v₁ = u₂

v₂ = 0

Kaatumisen jälkeen levossa olleen hiukkasen hankkii saman hiukkasen nopeuden, ja se puolestaan ​​pysähtyy.

Voi palvella sinua: hydraulinen paine

Kaksi erilaista massaa, yksi niistä alun perin levossa

Oletetaan tässä tapauksessa tai₁ = 0, Mutta massot ovat erilaisia:

Mitä jos m₁ on paljon suurempi kuin m₂?

Se tapahtuu, että m₁ Pysyä levossa ja m₂ Se palautetaan samalla nopeudella, jolla se vaikutti.

Huygens-Newton-palautuskerroin tai sääntö

Aikaisemmin johdettiin seuraava suhde kahden elastisen törmäyksen nopeuden välisistä suhteista: tai₁ - tai₂ = v₂ -  v₁. Nämä erot ovat suhteelliset nopeudet ennen törmäystä ja sen jälkeen. Yleensä törmäyksen vuoksi on toteutettu, että:

tai₁ - tai₂ = -(v₁ -  v₂-A

Suhteellista nopeuskonseptia arvostetaan paremmin, jos lukija kuvittelee, että se on yhdellä hiukkasista, ja tältä paikasta havaitsee nopeuden, jolla muut hiukkaset liikkuvat. Aikaisempi yhtälö kirjoitetaan uudelleen:

Jos kineettinen energia ei säilytetä, osoitettu osamäärä on alle 1. Soitetaan ja mainitun ulottumattoman osamäärän arvoon:

O No:

Arvo ja on välillä 0 ja 1 ja sitä kutsutaan palautuskerroin. Kun yhteentörmäys on joustava, e = 1. Kun se on täysin joustamaton, e = 0, vaikka sillä on muuta väliarvoa, jotkut kineettinen energia on hajonnut muun tyyppisissä energiaissa.

Ratkaisut

-Liikunta ratkaistiin 1

Biljardipallo liikkuu vasemmalle nopeudella 30 cm/s, törmää eteenpäin toisella identtisellä pallolla, joka siirtyy oikealle 20 cm/s. Molemmilla palloilla on sama taikina ja onnettomuus on täysin joustava. Etsi kunkin pallon nopeus iskun jälkeen.

Ratkaisu

tai₁ = -30 cm/s

tai₂ = +20 cm/s

Tämä on erityistapaus, että kaksi identtistä massaa törmäävät elastical -ulottuvuuteen, joten nopeudet vaihdetaan.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Liikunta ratkaistiin 2

Maassa pomppivan pallon palautuskerroin on yhtä suuri kuin 0,82. Jos putoat leposta, mikä osa alkuperäisestä korkeudestasi saavuttaa pallon kerran pomppimisen jälkeen? Ja 3 levypalloa?

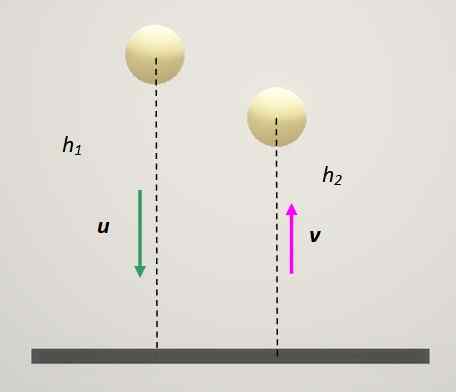Pallo pomppii tiukkaa pintaa vasten ja menettää korkeuden jokaisen palautumisen kanssa. Lähde: Itse tehty.

Ratkaisu

Maaperä voi olla esine 1 palautuskertoimen yhtälössä. Ja se on aina levossa, niin että:

Negatiivinen suunta valitaan ja positiivinen. Objektin nopeus, joka vapautetaan vapaasti tietystä korkeudesta h_jompikumpi On:

Merkki (-) osoittaa, että pallo laskeutuu:

Se voi palvella sinua: Torricelli -koe: Ilmakehän paineen mittaukset, merkitys

 

Tällä nopeudella pomppii:

 

+ Merkki osoittaa, että se on nouseva nopeus. Ja sen mukaan pallo saavuttaa enimmäiskorkeuden:

 

Nyt hän palaa maahan uudelleen saman suuruuden nopeudella, mutta vastakkainen merkki:

Ja pomppii:

Tämä saavuttaa enimmäiskorkeuden:

Saavuta maahan uudelleen:

Peräkkäiset levypallit

Joka kerta kun pallo pomppii ja nousee, sinun on kerrottava nopeus uudelleen 0: lla.82:

Ja saavuttaa maksimikorkeuden määritettynä mainitun nopeuden neliön perusteella:

Tässä vaiheessa h₃ on noin 30% h_jompikumpi. Mikä olisi korkeus 6. levypalloa ilman, että sinun on tehtävä niin yksityiskohtaisia ​​laskelmia kuin edelliset?

Minä olisin h₆ = 0.82¹² h_jompikumpi = 0.092H_jompikumpi tai vain 9% h_jompikumpi.

-Liikunta ratkaistiin 3

300 g lohko siirtyy pohjoiseen - 50 cm/s ja yhteenotto 200 g: n lohkoon, joka on suunnattu etelään 100 cm/s. Oletetaan, että yhteentörmäys on täysin joustava. Etsi nopeudet iskun jälkeen.

Tiedot

m₁ = 300 g; tai₁ = + 50 cm/s

m₂ = 200 g; tai₂ = -100 cm/s

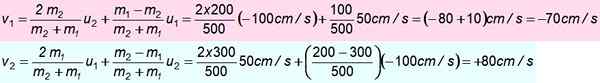
-Liikunta ratkaistiin 4

Massa m on vapautettu₁ = 4 kg radalla ilmoitetusta pisteestä ilman kitkaa, kunnes se törmää M: n kanssa₂ = 10 kg levossa. Mihin korkeus on m₁ Törmäyksen jälkeen?

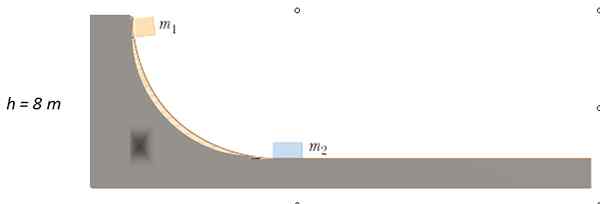
Ratkaisu

Koska kitkaa ei ole, mekaaninen energia säilyy nopeuden löytämiseksi tai₁ millä m₁ vaikutukset  m_2. Alun perin kineettinen energia on 0, koska m₁ osa lopusta. Kun siirryt vaakasuoralle pinnalle, sillä ei ole korkeutta, joten potentiaalienergia on 0.

MGH = ½ MU₁ ²

 

tai₂ = 0

Nyt nopeus m₁ Törmäyksen jälkeen:

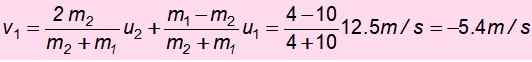
Negatiivinen merkki tarkoittaa, että se on palautettu. Tämän nopeuden noustessa ja mekaaninen energia säilytetään uudelleen H ', Korkeus, jolla se onnistuu nousemaan onnettomuuden jälkeen:

½ MV₁² = mgh '

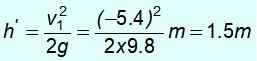
Huomaa, että et palaa lähtöpisteeseen 8 m korkeudella. Sillä ei ole tarpeeksi energiaa, koska se antoi osan kineettisestä energiastaan ​​massan m_1.

Viitteet

1. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fysiikan perusteet. Pearson. 135-155.
3. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Cengage -oppiminen. 172 -182
4. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti. 217-238
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. MacGraw Hill. 185-195