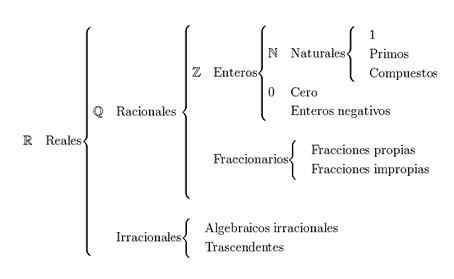
Reaalilukujen luokittelu

Pää Reaalilukujen luokittelu Se on jaettu luonnollisiin numeroihin, kokonaislukuihin, rationaalisiin lukuihin ja irrationaalisiin numeroihin. Todelliset numerot esitetään kirjaimella r.

Todelliset numerot viittaavat rationaalisten ja irrationaalisten lukujen ryhmien yhdistelmään. Näiden ryhmien muodostamiseksi tarvitaan luonnollisia lukuja ja kokonaisia ​​lukuja.

On olemassa monia tapoja, joilla erilaisia ​​todellisia lukuja voidaan rakentaa tai kuvata, vaihtelevat yksinkertaisemmista muodoista monimutkaisempiin muodoihin riippuen matemaattisesta työstä, jonka haluat suorittaa.

Kuinka todelliset numerot luokitellaan?

- Luonnolliset luvut

Luonnolliset luvut esitetään kirjaimella (n) ja niitä käytetään laskemaan (0,1,2,3,4 ...). Esimerkiksi "on viisitoista Rosas puutarhassa ”,“ Meksikon väestö on kotoisin 126 miljoonat ihmisistä "tai" kaksi ja kaksi On neljä". On huomattava, että jotkut luokitukset sisältävät 0 luonnollisena lukumääränä ja toiset eivät. 

Kaksi lasta, jotka tekevät kahden luonnollisen määrän summan.

Luonnolliset luvut eivät sisällä niitä, joilla on desimaaliosa. Siksi ”Meksikon väestö on kotoisin 126.2 Miljoonat ihmiset "tai" tekevät lämpötilan 24.5 Celsius astetta ”luonnollisia lukuja ei voitu harkita.

Yleisellä kielellä, kuten peruskoulut, luonnollisia lukuja voidaan kutsua kirjanpidonumeroiksi negatiivisten kokonaislukujen ja nollan sulkemiseksi pois.

Luonnolliset numerot ovat emäksiä, joilla monet muut numerosarjat voidaan rakentaa laajennuksella: kokonaisluvut, rationaaliset numerot, reaaliluku.

Luonnollisten lukujen, kuten ensisijaisten lukujen jakautumista ja jakautumista, on tutkittu lukujen teoriassa. Laskenta- ja tilaamiseen liittyvät ongelmat, kuten luettelot ja osiot, tutkitaan yhdistelmässä.

Heillä on useita ominaisuuksia, kuten: summa, kertolasku, vähennys, jako jne.

Voi palvella sinua: Nykytiede

Ordinaali- ja kardinaalinumero

Luonnolliset numerot voivat olla ordinaalia tai kardinaalia.

Kardinaaliset numerot olisivat niitä, joita käytetään luonnollisina lukuina, kuten edellä mainittiin esimerkeissä. "Omistaa kaksi evästeet "," olen isä kolme Lapset ”,“ laatikko sisältää kaksi Lahjavoiteet ". 

Ordaalit ovat ne, jotka ilmaisevat järjestyksen tai osoittavat aseman. Esimerkiksi kilpailussa voittaja on lueteltu juoksijoiden saapumisjärjestyksessä ja viimeisen päättyen maaliin tuli.

Tällä tavalla sanotaan, että voittaja on "ensimmäinen", seuraava "toinen", seuraava "kolmas" ja niin edelleen viimeiseen asti. Nämä numerot voidaan edustaa oikeassa yläkulmassa olevalla kirjaimella yksinkertaistaakseen kirjoitusta (1., 2., 3., 4., jne.-A.

- Kokonaisluvut

Koko numerot koostuvat niistä luonnollisista numeroista ja niiden vastakohdista, ts. Negatiiviset luvut (0, 1, -1, 2, -2, 50, -50 ...). Kuten luonnolliset luvut, nämä eivät sisällä niitä, joilla on desimaaliosa.

Esimerkki kokonaislukuista olisi "keskimäärin 30. sija Saksassa", "yöpyin 0: n saavuttaessani kuukauden lopun", "mennä alas kellariin, sinun on merkintä hissi -painike" hissin "".

Koko numeroa ei puolestaan ​​voida kirjoittaa murto -komponentilla. Esimerkiksi numerot, kuten 8.58 tai √2 eivät ole kokonaisia ​​lukuja.

Kokonaisluvut on esitetty kirjaimella (z). Z on rationaalisten lukujen alakortti Q, joka puolestaan ​​muodostaa Real N -lukujen ryhmän. Kuten luonnollinen lukumäärä, Z on ääretön kirjanpitoryhmä.

Kokonaisluvut muodostavat pienimmän ryhmän ja pienimmän joukon luonnollisia lukuja. Algebrallisissa luvut -teoriassa kokonaisia ​​lukuja kutsutaan joskus irrationaaliseksi erottamaan ne algebrallisista kokonaislukuista.

Se voi palvella sinua: tutkimusprojekti: Osapuolet, miten se on kehitetty ja esimerkki

- Rationaaliset numerot

Rationaalisten lukujen joukko on edustettuna kirjaimella (Q) ja sisällytä kaikki nämä numerot, jotka voidaan kirjoittaa murto -osaksi kokonaislukuista.

Toisin sanoen tämä sarja sisältää luonnolliset numerot (4/1), kokonaisluvut (-4/1) ja tarkat desimaalit (15,50 = 1550/100).

1/6 juuston jakautuminen on rationaalinen luku.

Rationaalisen luvun desimaalilaajennus päättyy aina äärellisen numeron (esim. 15.50) tai kun sama rajallinen numerojärjestys alkaa toistaa uudestaan ​​ja uudestaan ​​(esim. 0,345666666666666…). Siksi rationaalisten lukujen joukossa numerot sisällytetään. Puhtaat sanomalehdet tai sekoitetut sanomalehdet.

Lisäksi mikä tahansa toistuva tai terminaalinen desimaali edustaa rationaalista lukua. Nämä lausunnot ovat totta paitsi 10: lle, myös mille tahansa muulle tukikohdasta.

Todellista numeroa, jota ei ole järkevää, kutsutaan irrationaaliseksi. Irrationaaliset numerot sisältävät esimerkiksi √2, π ja e. Koska koko rationaalisten lukujen joukko on tunnottomaton ja että reaalilukujen ryhmä ei ole tunnottomaton, voidaan sanoa, että melkein kaikki todelliset numerot ovat irrationaalisia.

Järkevä lukumäärä voidaan määritellä muodollisesti kokonaisten parien ekvivalenssiluokiksi (p, q) siten, että q ≠ 0 tai vastaava suhde määrittelee (P1, Q1) (P2, Q2) vain jos P1, Q2 = P2Q1.

Rationaaliset numerot yhdessä summan ja kertolaskujen kanssa muodostavat kentät, jotka muodostavat kokonaiset numerot ja sisältävät minkä tahansa haaran, joka sisältää kokonaisuuden.

- Irrationaaliset numerot

Irrationaaliset numerot ovat kaikki todellisia lukuja, jotka eivät ole rationaalisia lukuja; Irrationaalisia lukuja ei voida ilmaista fraktioina. Rationaaliset numerot ovat lukuja, jotka koostuvat kokonaislukujen fraktioista.

Laulajakokeen seurauksena, jonka mukaan kaikki reaalilukut eivät ole käsittämättömiä ja että rationaalinen, jos ne ovat numeroita, voidaan päätellä, että melkein kaikki todelliset numerot ovat irrationaalisia.

Voi palvella sinua: etenemissuunta ja siirtymä

Kun kahden linjasegmentin säde on irrationaalinen luku, voidaan sanoa, että nämä linjasegmentit ovat mittaamattomia; tarkoittaen, että ei ole riittävästi pituutta, jotta jokainen heistä voisi olla ”mittaa” samanlaisella tietyllä kokonaislukulla.

Irrationaalisten lukujen joukossa ovat ympyräympyrän säde π sen halkaisijalle, Eulerin (E) lukumäärä, kultainen luku (φ) ja kahden neliöjuuri; Vielä enemmän, kaikki luonnollisten lukujen neliöjuuret ovat irrationaalisia. Ainoa poikkeus tästä säännöstä ovat täydelliset neliöt.

Voidaan havaita, että kun irrationaaliset luvut ilmaistaan ​​paikannustietoisesti numeroryhmässä (kuten desimaalilukuja), älä lopu tai toista.

Tämä tarkoittaa, että ne eivät sisällä numerosarjaa, toistoa, jolla esityslinja tehdään.

Irrationaalisen numeron PI yksinkertaistaminen.

Esimerkiksi: numeron π desimaalin esitys alkaa 3: lla.14159265358979, mutta ei ole rajallista numeroa, joka voi edustaa π tarkalleen, eikä niitä voida toistaa.

Todiste siitä, että rationaalisen numeron desimaalin laajenemisen on päätyttävä tai toistettava, on erilainen kuin todiste siitä, että desimaalilaajennuksen on oltava rationaalinen luku; Vaikka nämä testit ovat perus- ja hieman pitkiä, ne vievät jonkin verran työtä.

Yleensä matemaatikot eivät yleensä ota käsitettä "päättymisen tai toistamisen" määrittelemiseksi rationaalisen numeron käsitteen määrittelemiseksi.

Irrationaalisia lukuja voidaan käsitellä myös ei -jatkuvilla fraktioilla.

Viitteet

1. ClassifyNg Real Numbers. Toipunut chilimathista.com.
2. Luonnollinen luku. Toipunut Wikipediasta.org.
3. Numeroiden luokittelu. Ditutor toipunut.com.
4. Toipunut Wikipediasta.org.
5. Irrationaaliluku. Toipunut Wikipediasta.org.