Kuinka saada prosenttiosuus? Esimerkkejä ja harjoituksia

Tölkki saada prosenttiosuus Useilla menetelmillä. Voit laskea nopeasti 10% mistä tahansa lukumäärästä vain siirtämällä desimaalilaitettasi vasemmalle. Esimerkiksi 10% 100: sta on 10; 10% 1000 on 100.

Jos haluat laskea monimutkaisempia prosenttimääriä, kuten 36% 25: stä tai 250%: sta 20: stä, tarvitaan muita menetelmiä. Tapauksissa, joissa 10%: n järjestelmää ei voida soveltaa, seuraavat menetelmät voidaan ottaa huomioon.

Kuvio 1. Alennukset eri prosenttimäärillä. Kuinka paljon säästämme toisiamme?. Lähde: Pixabay.

Termi prosenttiosuus tarkoittaa tiettyä osaa jokaisesta sadasta ja viittaa aritmeettiseen operaatioon, joka suoritetaan mainittua osan löytämiseksi. Esimerkiksi 20% (“Kaksikymmentä prosenttia”) luetaan pesossa, se tarkoittaa, että 20 pesoa alennetaan jokaisesta 100 pesosta.

Prosenttiosuus laskee, mikä osa kokonaismäärästä edustaa määrää. Tässä tapauksessa kokonaismäärä siirretään asteikkoon 100 ja prosenttiosuus ilmoittaa, kuinka paljon näiden 100: n perusteella on laskettava osa.

Katsotaanpa, miten se tehdään näiden esimerkkien kanssa. Ensinnäkin teemme sen murto -osan muodossa:

• 20% = 20/100
• 5% = 5/100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Huomaa, että 100% on yhtä suuri kuin 1. Mutta prosenttiosuudet voidaan kirjoittaa myös desimaaliin:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Kun tietyn määrän prosenttiosuus ilmaistaan, yksinkertaisesti Pilkku liikkuu Tästä numerosta kaksi paikkaa vasemmalle. Prosentuaalisesti, suhteellisuussääntö-

20% on 20 100: sta, siksi:

20% 100: sta on 20, 20% 200 on 40, 20% 300: sta on 60, 20% 50: stä on 10.

Yleinen sääntö 20 prosentilla mistä tahansa määrästä

20% x: stä on x *(20/100) = x *0,2 = 0,2 *x

Tämä sääntö voi helposti ulottua löytämään minkä tahansa muun halutun prosenttiosuuden. Katsotaan kuinka seuraavassa osassa.

Liikunta on ratkaistu kaavalla N%: n laskemiseksi 

Kaava, joka on tiivistettävä mahdollisimman pian ja lasketaan nopeasti mikä tahansa prosenttiosuus n On:

n % =(A * n)/100

Esimerkiksi haluat laskea 25% 400: sta

Sitten n = 25 ja A = 400, mikä johtaa (400*25)/100 = 100

Esimerkki

Mikä prosenttiosuus 60 on 24?

Ratkaisu

Pyydetään vastaava, mikä on 60: n N%, joka antaa 24?

Ehdotamme yleistä kaavaa:

60 * N / 100 = 24

Me tyhjentämme n Tällä menettelyllä:

-100, joka jakautuu jäseneksi IZiédo Tasa -arvoinen, mene jäsenelle oikea moninkertainen. 

-Ja 60, joka kertoo jäsenestä vasen Mennä jäseneksi oikea jakava.

N = 24 *100/60 = 2400/60 = 240/6 = 6 *40/6 = 40

Päätelee, että 40% 60: stä on 24.

Ratkaistu prosentuaalinen laskentaharjoitukset 

Alla on yksinkertaisia ​​harjoituksia edellä mainitun harjoittamisen aloittamiseksi.

Se voi palvella sinua: 15 suosituinta legendoa ja myyttiä

Harjoitus 1

Löydä 50% 90: stä.

Ratkaisu

Tässä x = 90, n = 50 % ja korvaa:

90 * 50% = 90 * (50/100) = 4500/100 = 45 

Tämä on melko yksinkertaista, koska 50 % mistä tahansa määrästä on puolet tästä määrästä ja puolet 90: stä on 45.

Harjoitus 2

Löydä 30% 90: stä.

Ratkaisu

90 * 30% = 90 * (30/100) = 2700/100 = 27

Prosenttiosuus kasvaa

Jokapäiväisessä elämässä on usein kuunnella jonkin, esimerkiksi tuotannon lisääntymistä, palkankorotusta tai tuotteen nousua. Se ilmaistaan ​​melkein aina prosentteina.

Esimerkiksi tietty tuote maksaa 300 euroa, mutta se sai nousun 30%. Kysymme itseltämme: mikä on uusi tuotteen hinta?

Ensimmäinen on laskea osa, joka vastaa kasvua. Koska lisäys on 30 osaa 100: sta, joten nousun nousu alkuperäisen 300 hinnan perusteella on kolme kertaa 30 osaa, eli 3*30 = 90.

Tuote nousi 90 euroa, joten uusi lopullinen hinta on se, mikä maksaa lisäyksen aiemmin:

Uusi hinta = vanha hinta + 90 € = 390 €

Voimme rakentaa kaavan prosentuaalisen kasvun laskemiseksi. Käytämme kirjeitä hintojen symboloimiseksi, kuten tämä:

-F on lopullinen arvo

-Yllyttää on alkuarvo ja

-n on kasvun lisääntyminen.

Näiden nimien kanssa lopullinen arvo lasketaan näin:

f = i + (i* n / 100)

Mutta miten Yllyttää Se toistetaan molemmissa termeissä, sitä voidaan pitää yleisenä tekijänäTämän toisen lausekkeen saamiseksi, yhtä pätevä:

F = i * (1 + n / 100)

Varmistetaan jo ratkaistu tapaus, tuote, joka maksoi 300 euroa ja kasvoi 30%. Siksi varmistamme, että kaava toimii hyvin:

Lopullinen hinta = f = 300 € * (1 + 30/100) = 300 € * (1 + 0,3) = 300 € * 1,3 = 390 €

Harjoitus 3

Työntekijä ansaitsi 1500 euroa, mutta häntä ylennettiin ja hänen palkansa lisäys 20%. Mikä on uusi palkkasi?

Ratkaisu

Sovelletaan kaava:

F = 1500 € * (1 + 20/100) = 1500 € * (1 + 0,2) = 1500 € * 1,2 = 1800 €

Uusi työntekijän palkka on 1800 euroa.

Prosenttiosuus laskee

Laskujen tapauksessa lopullisen arvon laskemiseksi kaava F tietyn alkuperäisen määrän Yllyttää Se kärsi vähentyessä n% On:

F = i * (1 - n / 100)

On huomattava, että edellisen osan kaavan positiivinen merkki (+) korvattiin negatiivisella merkillä (-).

Kuva 2. Prosenttiosuus alennusilmoitus. Lähde: Pixabay

Harjoitus 4

Tuote oli 800 euroa, mutta sai 15% alennuksen. Mikä on uusi tuotteen hinta?

Ratkaisu 4

Lopullinen hinta kaavan mukaan on:

F = 800 € * (1 - 15/100) = 800 € * (1 - 0,15) = 800 € * (0,85) = 680 €

Lopullinen hinta 15%: n alennuksella on 680 euroa, mikä edustaa 120 euron säästöä.

Peräkkäiset prosenttimäärät

Vaikuttaa siltä, ​​kun jokin määrä kärsii prosentuaalinen vaihtelu ja sitten toinen sovelletaan, myös prosenttiosuus. Esimerkiksi tuote, jolla on ollut kaksi prosenttia alennusta peräkkäin. Toinen esimerkki on työntekijä, jolla oli kaksi peräkkäistä palkankorotusta.

Voi palvella sinua: tärkeämpi yucatanin taloudellinen toiminta

- Peräkkäinen prosenttiosuus kasvaa

Näiden tapausten ratkaisupohja on sama kuin ainutlaatuiset nousut, mutta on otettava huomioon, että toisen prosentuaalinen lisäys suoritetaan ensimmäisen lisäyksen lopulliseen arvoon.

Oletetaan, että tuote nousi ensimmäisellä 10%: lla ja sitten 5%. On väärin sanoa, että se kärsi 15%: n kasvusta, se oli oikeastaan ​​enemmän kuin tämä prosenttiosuus.

Lopullisen arvon kaavat sovelletaan näin:

-Ensinnäkin N1%: n ensimmäisen nousun lopullinen arvo lasketaan

f1 = i + i * n1 / 100

-Ja sitten, jotta löydetään N2%: n toisen lisäyksen lopullinen arvo F1: n lopullinen arvo otetaan alkuperäiseksi arvoksi. Siksi:

F2 = f1 + f1 * n2 /100 

Harjoitus 5

Kirja maksoi alun perin 55 euroa, mutta menestyksensä ja korkean kysynnän vuoksi se kärsi kaksi peräkkäistä korotusta alkuperäisestä hinnasta. Ensimmäinen lisäys oli 10% ja toinen 20%. Mikä on kirjan lopullinen hinta?

Ratkaisu

-Ensimmäinen lisäys:

F1 = 55 € * (1 + 10/100) = 55 € * 1,1 = 60,5 €

-Toinen lisäys

F2 = 60,5 € * (1 + 20/100) = 60,5 € * 1,2 = 72,6 €

Lopullinen hinta on 72,6 euroa.

Harjoitus 6

Viitaten edelliseen harjoitukseen. Kaksi peräkkäistä nousua?

Ratkaisu

Jos kutsumme N% ainutlaatuisen lisäyksen prosenttimääräksi, kaava, joka liittyy tämän ainutlaatuisen prosentuaalisen nousun alkuperäiseen arvoon ja lopullinen arvo on:

F2 = i *(1 + n / 100) 

Tarkoittaen:

72,6 € = 55 € + 55 € * (N / 100)

Kasvun kasvun tyhjentäminen n% = (N /100), meillä on:

(N / 100) = (72,6 € - 55 €) / 55 € = 17.6 € / 55 € = 0,32

Siksi:

N = 0,32 * 100 = 32

Kirjan hinnalla käytettiin kokonaisprosentin kasvua 32%. Huomaa, että tämä lisäys on suurempi kuin kahden peräkkäisen prosenttiosuuden summa kasvaa.

- Peräkkäiset prosenttiosuusalennukset

Idea on samanlainen kuin peräkkäisen prosentuaalinen osuus. Toinen prosenttiosuus alennusta on aina sovellettava ensimmäisen alennuksen lopulliseen arvoon, katsotaanpa esimerkki:

Harjoitus 7

10%: n alennus, jota seuraa toinen 20%: n alennus objektille, johon se on vastaava ainutlaatuinen prosenttimäärä alennus?

Ratkaisu

-Ensimmäinen alennus:

F1 = i - i * n1 / 100  

-Toinen alennus

F2 = f1 - f1 * n2 / 100

Ensimmäisen yhtälön korvaaminen toisessa on:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Tämän ilmaisun kehittämisessä saamme:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Piirrä yhteinen tekijä Yllyttää-

f2 = i * (1- N1% - N2% + N1% * N2%)

Lopuksi korvataan kysymyksessä ilmoitetut prosenttimäärät:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100 /100) = i * (1 - 28%)

Toisin sanoen peräkkäiset 10%: n ja 20%: n alennukset vastaavat ainutlaatuista 28% alennusta.

Edistyneet harjoitukset

Kokeilemme näitä harjoituksia vain, kun edellisten ideot ovat olleet riittävän selviä.

Se voi palvella sinua: helppoja ja kauniita maantieteen kannet, kannet, kuvat

Harjoitus 8

Kolmion pohja on 10 cm ja korkeus 6 cm. Jos pohjapituus pienenee 10%. Missä prosenttiosassa korkeutta tulisi lisätä, jotta kolmion pinta -ala ei muutu?

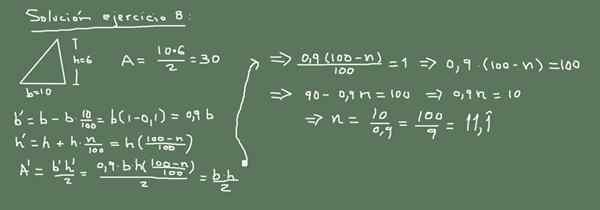Kuva 3. Vaihtoehtoinen ratkaisu harjoitukseen 8. Valmistettu f. Zapata.

Ratkaisu 8

Alkuperäinen kolmioalue on:

A = (10 cm * 6cm) / 2 = 30 cm²

Nyt, jos pohja laskee 10%, sen uusi arvo on:

Uusi pohja = 10 - (10/100) x 10 = 9 cm.

Uusi korkeusarvo on X, ja alkuperäinen alue on pidettävä ennallaan, joten:

(9cm * x) /2 = 30 cm²

Sitten x: n arvo tyhjennetään seuraavasti:

X = 60 cm² / 9 cm = (20/3) cm = 6 666 cm

Mikä tarkoittaa nousua 0,666 alkuperäiseen arvoon verrattuna. Katsotaanpa nyt, mikä prosenttiosuus tästä edustaa:

6 666 = 6 + (6 * N/100) 

6 666 -6 = 6 * N/100

0 -.666 = 6 * N/100

N/100 = 0,111

N = 11,1

Vastaus on: Korkeutta on lisättävä 11,1%, jotta kolmioalue pysyy samana.

Harjoitus 9

Jos palkkaa korotetaan 20%, mutta sitten vero -alennukset 5%, mikä on todellinen lisäys, jonka työntekijä saa?

Ratkaisu 

Ensin lasketaan N1%: n lisäys:

f1 = i + i * n1 / 100

Sitten käytämme N2%: n alennusta:

F2 = f1 - f1 * n2 / 100

Ensimmäinen yhtälö korvataan toisessa:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Edellinen ilmaus kehittyy:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Lopuksi se poistetaan Yllyttää Yleinen tekijä ja N1 = 20: n ja N2 = 5: n arvot, jotka ilmestyvät lauseeseen, korvataan:

F2 = i (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

Työntekijä sai nettokorotuksen 14%.

Harjoitus 10

Päätä, mikä on kätevin näiden kahden vaihtoehdon välillä:

i) hanki t -paidat 32 %: n alennuksella jokainen.

Ii) Osta 3 t -pakettia hintaan 2.

Ratkaisu 

Analysoimme jokaisen vaihtoehdon erikseen ja valitsemme sitten taloudellisimman:

i) Olkoon x paidan nykyinen hinta, 32 %: n alennus edustaa XF: n lopullista hintaa:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Esimerkiksi 3 paidan ostaminen tarkoittaa 3 x 0: n kuluttamista.68 x = 2.04x

ii) Jos x on paidan hinta, 3 paitaa varten maksat vain 2x.

Oletetaan, että paita on 6 euron arvoinen, 32 %: n alennuksella se olisi 4 -arvoinen.08 euroa. Osta 1 t -paaita ei ole kelvollinen vaihtoehto 3 × 2 -tarjouksessa. Joten jos haluat ostaa vain yhden paita, alennus on parempi.

Mutta jos haluat ostaa kymmenille, 3 × 2 -tarjous on vain vähän halvempi. Esimerkiksi 6 T -paidat alennuksella menisivät 24.48 euroa, kun taas 3 × 2 -tarjouksessa ne maksaisivat 24 euroa

Viitteet

1. Helppo luokkahuone. Prosenttiosuus. Haettu: luokkahuone.com
2. Kalku a. 2006. Käytännöllinen teoreettinen aritmeettinen. Kulttuuriversiot.
3. Educa Kids. Kuinka oppia laskemaan prosenttimäärät. Toipunut: Educapeques.com
4. Gutiérrez, G. Financial Mathematics Lutes. Toipunut: csh.Izt.Ura.MX
5. Älykkäät punkit. Prosenttiosuus: Mikä on ja miten lasketaan. Toipunut: Smartck.On