Korrelaatiokertoimen kaavat, laskenta, tulkinta, esimerkki

Hän korrelaatiokerroin Tilastoissa on indikaattori, joka mittaa kahden kvantitatiivisen muuttujan x ja y suuntauksen, jotta niiden välillä on lineaarisuus tai suhteellisuus.

Yleensä muuttujien parit x ja y ovat saman populaation kaksi ominaisuutta. Esimerkiksi x voi olla ihmisen e ja sen painon korkeus.

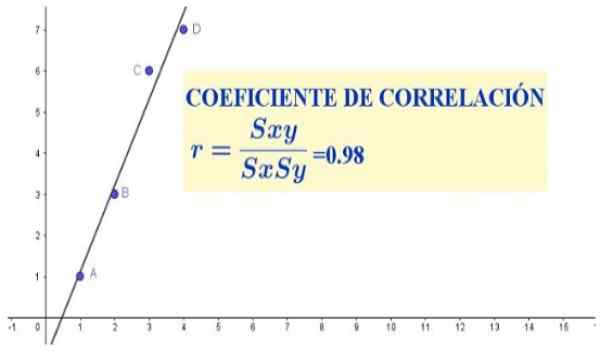
Kuvio 1. Korrelaatiokerroin neljälle dataparille (x, y). Lähde: f. Zapata.

Tässä tapauksessa korrelaatiokerroin osoittaisi, onko tietyn populaation korkeuden ja painon välillä suhteellisuus.

Pearsonin lineaarinen korrelaatiokerroin merkitään kirjaimella r - Pienet kirjaimet ja sen minimi- ja maksimiarvot ovat vastaavasti -1 ja +1. 

Arvo r = +1 osoittaisi, että koko parit (x, y) ovat täysin linjassa ja että X kasvaa ja kasvaa samassa osassa. Toisaalta, jos tapahtuu, että r = -1, myös parien joukko olisi täysin linjassa, mutta siinä tapauksessa, kun X kasvaa, ja pienenee samassa osassa.

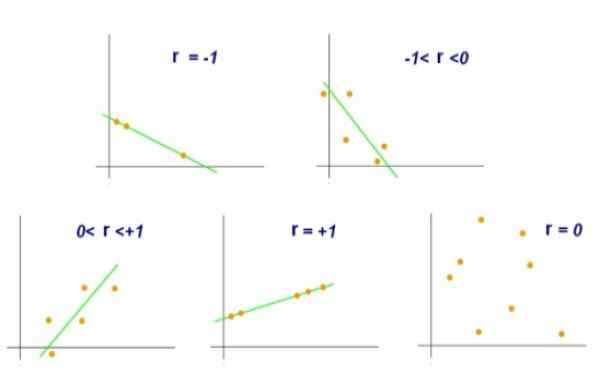Kuva 2. Lineaarisen korrelaatiokertoimen eri arvot. Lähde: Wikimedia Commons.

Toisaalta arvo r = 0 osoittaisi, että muuttujien x ja y välillä ei ole lineaarista korrelaatiota. Vaikka arvo r = +0,8 osoittaisi, että parit (x, y) yleensä ryhmittyvät toiselle ja toiselle tietylle viivalle.

Kaava korrelaatiokertoimen R laskemiseksi on seuraava:

Jos numeraattori edustaa muuttujien X ja Y.

Kuinka laskea korrelaatiokerroin?

Lineaarinen korrelaatiokerroin on tilastollinen määrä, joka sisällytetään tieteellisiin laskuriin, useimmissa laskentataulukoissa ja tilastollisissa ohjelmissa.

Voi palvella sinua: Hyperbolinen paraboloidi: Määritelmä, ominaisuudet ja esimerkit

On kuitenkin kätevää tietää, kuinka sitä määrittelevä kaava käytetään, ja tälle näkyy yksityiskohtainen laskelma, joka suoritetaan pienellä tietojoukolla.

Ja kuten edellisessä osassa todetaan, korrelaatiokerroin on SXY -kovarianssi jaettuna muuttujien ja muuttujien standardipoikkeama SX: n tuotetta muuttujalle ja SY: lle.

Kovarianssi ja varianssi

SXY -kovarianssi on:

Sxy = [σ (xi -) (yi -)] / (n -1)

Missä summa menee 1: stä N -pareihin (xi, yi). E ovat datan aritmeettiset sukat xi e yi.

Muuttujan x keskihajonta on puolestaan ​​XI -tietojoukon varianssin neliöjuuri, I: stä 1: stä n:

Sx = √ [σ (xi -)^2) / (n -1)]

Samoin muuttujan keskihajonta ja YI -tietojoukon varianssin neliöjuuri, I: stä 1: stä n:

SY = √ [σ (yi -)² ) / (N-1)]

Havainnollistava tapaus

Korrelaatiokertoimen laskemiseksi yksityiskohtaisesti, että otamme seuraavan joukon neljä tietoparia 

(X, y): (1, 1); (23); (3, 6) ja (4, 7).

Ensin lasketaan aritmeettinen keskiarvo x: lle ja y: lle, seuraavasti:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Sitten jäljellä olevat parametrit lasketaan:

Sxy -kovarianssi

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Voi palvella sinua: johdannaisäännöt (esimerkkien kanssa)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Vakiopoikkeama SX

SX = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Keskihajonta SY

SX = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Kaiteen kerroin r

R = 3.5 / (1.29 * 2.75) = 0 -.98

Tulkinta

Edellisen tapauksen tietojoukossa on vahva lineaarinen korrelaatio muuttujien X ja Y: n välillä, mikä ilmenee sekä dispersiokaaviossa (joka voidaan nähdä kuvassa 1) että korrelaatiokertoimessa, joka heitti arvon melko lähellä sitä yksikkö.

Sikäli kuin korrelaatiokerroin on lähempänä 1 tai -1, järkevämpi tekee tietojen asettamisesta linjalle, lineaarisen regression tulos.

Lineaarinen regressio

Lineaarinen regressioviiva saadaan Menetelmä vähiten neliöitä. jossa regressioviivaparametri saadaan arvon ja arvioidun eron neliön summan minimoinnista ja N -datan YI: n välillä.

Toisaalta regressioviivan Y = A + BX: n parametrit A ja B, jotka on saatu minimiluumien menetelmällä, ovat:

*B = sxy / (sx²) Rinteessä

*A = - b regressioviivan leikkauspisteeseen ja akselin kanssa.

Muista, että SXY on yllä määritelty kovarianssi ja SX² Se on aikaisemmin määritellyn keskihajonnan varianssi tai neliö. E ovat datan x ja vastaavasti aritmeettiset keinot.

Esimerkki

Korrelaatiokerrointa käytetään määrittämään, onko kahden muuttujan välillä lineaarinen korrelaatio. Se on sovellettavissa, kun tutkitut muuttujat ovat kvantitatiivisia ja myös niiden on tarkoitus seurata normaalia tyyppistä jakaumaa.

Voi palvella sinua: toiminnon kirjeenvaihtosääntö

Havainnollistava esimerkki, joka meillä on alla: liikalihavuuden asteen mitta on kehon massaindeksi, joka saadaan jakamalla yhden ihmisen paino kilogrammoihin saman korkeuden välillä neliöyksiköissä neliöön.

Halutaan tietää, onko kehon massaindeksin ja veressä HDL -kolesterolin pitoisuuden välillä vahva korrelaatio mitattuna millimoleina litrassa. Tätä varten on tehty tutkimus 533 ihmisen kanssa, jotka on esitetty seuraavassa kaaviossa, jossa kukin piste edustaa ihmisen tietoja.

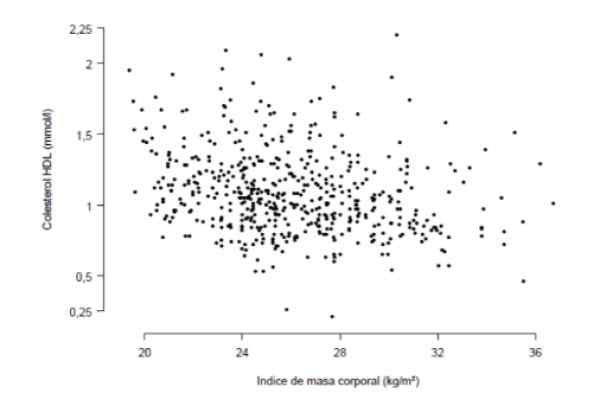Kuva 3. IMC -tutkimus ja HDL -kolesteroli 533 potilaalla. Lähde: Aragonese Institute of Health Sciences (IACS).

Kaavion huolellisesta havainnosta seuraa, että HDL -kolesterolipitoisuuden ja kehon massaindeksin välillä on tietty lineaarinen (ei kovin merkitty) suuntaus. Tämän suuntauksen kvantitatiivinen mitta on korrelaatiokerroin, joka tässä tapauksessa osoittautui r = -0,276.

Viitteet

1. González c. Yleiset tilastot. Toipunut: Tarwi.La Molina.Edu.PE -PE
2. IACS. Aragonese Institute of Health Sciences. Haettu: ICS-Aragon.com 
3. Salazar C. ja Castillo S. Perustilastot periaatteet. (2018). Haettu osoitteesta: dspace.Uce.Edu.EY
4. Superprof. Korrelaatiokerroin. Toipunut: SuperProf.On
5. USAC. Kuvaileva tilastokäsikirja. (2011). Palautettu: Tilastot.tekniikka.USAC.Edu.GT
6. Wikipedia. Pearson -korrelaatiokerroin. Palautettu: on.Wikipedia.com.