Poisson -jakaumakaavat, yhtälöt, malli, ominaisuudet

Se Poisson -jakelu Se on erillinen todennäköisyysjakauma, jonka kautta voit tietää todennäköisyyden, että suuren näytteen sisällä ja tietyn ajan aikana tapahtuma, jonka todennäköisyys on pieni.

Usein Poissonin jakautumista voidaan käyttää binomijakauman sijasta, kunhan kuvattuja olosuhteita täytetään: suuri näyte ja pieni todennäköisyys.

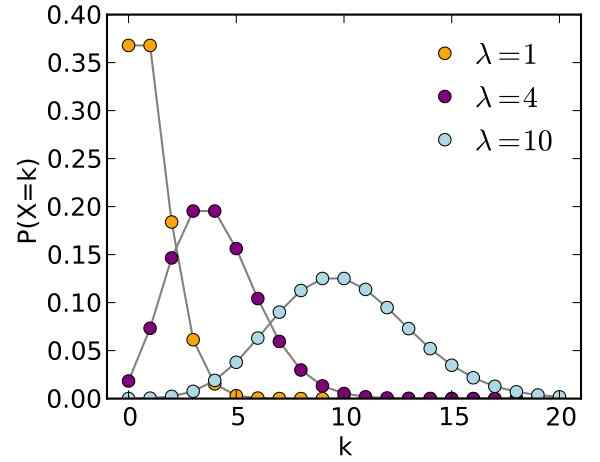
Kuvio 1. Poisson -jakelukaavio eri parametreille. Lähde: Wikimedia Commons.

Siméon-Denis Poisson (1781-1840) loi tämän jakelun, joka kantaa hänen nimensä, erittäin hyödyllinen arvaamattomien tapahtumien suhteen. Poisson julkaisi tuloksensa vuonna 1837, tutkimustyö virheellisten rikoslauseiden todennäköisyydestä.

Myöhemmin muut tutkijat mukauttivat jakautumisen muilla alueilla, esimerkiksi niiden tähten lukumäärän, jotka voivat olla tietyssä tilassa, tai todennäköisyys, että sotilas kuolee hevosen cozin takia.

[TOC]

Kaava ja yhtälöt

Poissonin jakelun matemaattinen muoto on seuraava:

 - Satunnaismuuttuja on ja

- μ (myös joskus nimeltään λ) Se on keskimääräinen tai jakeluparametri

- Euler -numero: E = 2.71828

- Y = k: n saamisen todennäköisyys on P

- k -k - Se on menestysten lukumäärä 0, 1,2,3 ..

- n Se on testien tai tapahtumien lukumäärä (näytteen koko)

Diskreetti satunnaismuuttujat, kuten nimestä voi päätellä, riippuvat sattumasta ja ottavat vain erilliset arvot: 0, 1, 2, 3, 4 ..., k.

Jakauman keskiarvo on antanut:

Σ -varianssi, joka mittaa datan dispersiota, on toinen tärkeä parametri. Poissonin jakeluun se on:

σ = μ

Poisson päätti, että kun n → ∞ ja p → 0, keskimääräinen μ -myös kutsuttu odotettu arvo- Se on taipumus vakiona:

μ → vakio

Tärkeä- p Se on tapahtuman esiintymisen todennäköisyys ottaen huomioon kokonaisväestö, kun taas P (y) Se on Poissonin ennuste näytteestä.

Malli ja ominaisuudet

Poissonin jakautumisella on seuraavat ominaisuudet:

-Näytteen koko on suuri: N → ∞.

-Tarkasteltuja tapahtumia tai tapahtumia ovat toisistaan ​​riippumattomia ja tapahtuvat satunnaisesti.

-Todennäköisyys P Mikä tietty tapahtuma ja Se tapahtuu tietyn ajanjakson ajan on hyvin pieni: P → 0.

-Usean kuin yhden tapahtuman todennäköisyys aikavälillä on 0.

-Keskiarvo on lähellä: μ = n.P (n on näytteen koko-A

-Koska dispersio σ on yhtä suuri kuin μ, koska se ottaa suurempia arvoja, myös vaihtelu on suurempi.

-Tapahtumat on jaettava tasaisesti käytetyllä aikavälillä.

-Mahdollisten tapahtuma -arvojen joukko ja Se on: 0,1,2,3,4 .. .

Voi palvella sinua: Satunnainen koe: Konsepti, näytetila, esimerkkejä

-Summa Yllyttää Muuttujat, jotka seuraavat Poisson -jakaumaa, ovat myös toinen Poisson -muuttuja. Sen keskiarvo on näiden muuttujien keskiarvojen summa.

Erot binomiaalisen jakautumisen kanssa

Poissonin jakauma eroaa binomien jakautumisesta seuraavissa tärkeissä näkökohdissa:

-Binomiin jakautumiseen vaikuttaa sekä S -näytteen koko että todennäköisyys P, Mutta Poissonin jakautumiseen vain keskimäärin μ.

-Binomijakaumassa satunnaismuuttujan mahdolliset arvot ja Ne ovat 0,1,2,…, sen sijaan Poissonin jakautuessa näille arvoille ei ole ylärajaa.

Esimerkit

Poisson sovelsi alun perin kuuluisaa jakeluaan oikeudellisiin tapauksiin, mutta teollisuustasolla yksi sen ensimmäisistä käytöistä oli oluen valmistuksessa. Tässä prosessissa hiivakasveja käytetään käymiseen.

Hiiva koostuu elävistä soluista, joiden populaatio on vaihteleva ajassa. Oluen valmistuksessa on tarpeen lisätä tarvittava määrä, joten on tarpeen tietää solujen määrä tilavuusyksikköä kohti.

Toisen maailmansodan aikana Poissonin jakelua käytettiin tietämään, osoittavatko saksalaiset todella Lontooseen Calaisista vai vain ampuen satunnaisesti. Tämä oli tärkeää liittolaisille selvittää, kuinka hyvä se oli natsien käytettävissä oleva tekniikka.

Käytännölliset sovellukset

Poissonin jakelusovellukset viittaavat aina aikasuunnitelmiin tai avaruuslaskuihin. Ja koska esiintymisen todennäköisyys on pieni, se tunnetaan myös "harvinaisten tapahtumien laki".

Tässä on luettelo tapahtumista, jotka kuuluvat johonkin näistä luokista:

-Hiukkasten rekisteröinti radioaktiiviseen rappeutumiseen, joka kuten hiivasolujen kasvu, on eksponentiaalinen funktio.

-Vierailujen lukumäärä tiettyyn verkkosivustoon.

-Ihmisten saapuminen riviin maksamaan tai osallistumaan (hännän teoria).

-Autojen lukumäärä, jotka kulkevat tiellä tietyn ajankohdan läpi tietyn ajanjakson ajan.

Kuva 2. Pisteen läpi kulkevien autojen määrä seuraa suunnilleen Poisson -jakautumista. Lähde: Pixabay.

-Mutaatiot kärsivät tietyssä DNA -ketjussa säteilylle altistumisen jälkeen.

-Halkaisijan meteorinumero yli 1 m vuodessa vuodessa.

-Viat neliömetriä kohti kangasta.

-Verisolujen määrä yhdellä kuutiolla senttimetrillä.

-Puhelut minuutissa puhelinvaihtoon.

-Suklaa kipinät läsnä 1 kg kakku taikinaa.

-Puiden lukumäärä, joka on tartunnan saanut yhden hehtaarin metsä.

Huomaa, että nämä satunnaismuuttujat edustavat kuinka monta kertaa tapahtuma tapahtuu kiinteäksi ajaksi (Puhelut minuutissa puhelinvaihtoon) tai tietty avaruusalue (Kankaan viat neliömetriä kohti-A.

Voi palvella sinua: suhteellinen variaatio

Nämä tapahtumat, kuten jo vahvistetaan, ovat riippumattomia siitä ajasta, joka on kulunut viimeisestä tapahtumasta.

Lähestyen binomijakaumaa Poissonin jakauman kanssa

Poissonin jakauma on hyvä lähestymistapa binomiaaliseen jakautumiseen niin kauan kuin:

-Näytteen koko on suuri: n ≥ 100

-Todennäköisyys P on pieni: P ≤ 0,1

- μ olla: NP ≤ 10

Tällaisissa tapauksissa Poissonin jakauma on erinomainen työkalu, koska binomialusta voi tulla monimutkaiseksi soveltaa näissä tapauksissa.

Ratkaisut

Harjoitus 1

Seismologisessa tutkimuksessa todettiin, että viimeisen 100 vuoden aikana maailmanlaajuisesti oli 93 suurta maanjäristystä, vähintään 6.0 RICHTER -Slogaritmisessa asteikolla-. Oletetaan, että Poissonin jakauma on tässä tapauksessa riittävä malli. Löytö:

a) Suurten maanjäristysten keskimääräinen esiintyminen vuodessa.

b) Kyllä P (y) Se on todennäköisyys tapahtua ja Maanjäristykset satunnaisesti valitulle vuodelle löydä seuraavat todennäköisyydet:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) ja P (7).

c) Tutkimuksen todelliset tulokset ovat seuraavat:

- 47 vuotta (0 maanjäristystä)

- 31 vuotta (1 maanjäristys)

- 13 vuotta (2 maanjäristystä)

- 5 vuotta (3 maanjäristystä)

- 2 vuotta (4 maanjäristystä)

-  0 vuotta (5 maanjäristystä)

- 1 vuotta (6 maanjäristystä)

- 1 vuotta (7 maanjäristystä)

Kuinka nämä tulokset saadaan B alakohdassa B? On Poissonin jakelu hyvä valinta mallintaa näitä tapahtumia?

Ratkaisu)

a) Maanjäristykset ovat tapahtumia, joiden todennäköisyys p Hän on pieni ja harkitsemme rajoitettua ajanjaksoa, yhden vuoden. Keskimääräiset maanjäristykset ovat:

μ = 93/100 maanjäristykset / vuosi = 0.93 maanjäristystä vuodessa.

Ratkaisu b)

b) Pyydettyjen todennäköisyyksien laskemiseksi arvot korvataan alussa annetussa kaavassa:

Esimerkiksi löytää P (2), Mikä olisi todennäköisyys, että maanjäristykset ovat 2 suurta vuodessa:

y = 2

μ = 0.93

E = 2.71828

Ja tämä on todennäköisyys, että vuoden ajan on 7 suurta maanjäristystä:

Se on melko pienempi kuin P (2).

Tulokset on lueteltu alla:

P (0) = 0.395, P (1) = 0.367, P (2) = 0.171, P (3) = 0.0529, P (4) = 0.0123, P (5) = 0.00229, P (6) = 0.000355, P (7) = 0.0000471.

Voisimme esimerkiksi sanoa, että todennäköisyys on 39.5 %, että suurta maanjäristystä ei tapahdu tietyn vuoden aikana. Tai että on 5,29 %, että 3 suurta maanjäristystä tapahtuu sinä vuonna.

Liuos c)

c) Taajuudet analysoidaan kertomalla n = 100 vuotta:

39.5; 36.7; 17.1; 5.29; 1.23; 0 -.229; 0 -.0355 ja 0.00471.

Voi palvella sinua: algebralliset johdannaiset

Esimerkiksi:

- Taajuus 39.5 osoittaa, että 39: ssä.Viisi 100 vuotta vanhoja tai suuria maanjäristyksiä tapahtuu, voimme sanoa, että se on melko lähellä todellista 47 -vuotista tulosta ilman suurta maanjäristystä.

Vertaamme toista Poisson -tulosta todellisiin tuloksiin:

- Arvo 36: sta.7 tarkoittaa, että 37 vuoden aikana on yksi suuri maanjäristys. Todellinen tulos on, että 31 vuoden aikana oli yksi suuri maanjäristys, hyvä sattuma malliin.

- 17 odotetaan.1 vuotta 2 suurella maanjäristyksellä ja tiedetään, että 13 vuoden aikana, mikä on läheinen arvo, oli voimassa 2 suuria maanjäristyksiä.

Siksi Poisson -malli on hyväksyttävä tässä tapauksessa.

Harjoitus 2

Yritys arvioi, että epäonnistuneiden komponenttien lukumäärä ennen 100 toiminnan suorittamista seuraa Poisson -jakelu. Jos vikojen keskimääräinen lukumäärä on tuolloin 8, etsi seuraavat todennäköisyydet:

a) että komponentti epäonnistuu 25 tunnissa.

b) Vika alle kaksi komponenttia, 50 tunnissa.

c) Ainakin kolme komponenttia epäonnistuu 125 tunnissa.

Ratkaisu)

a) Tiedetään, että keskimääräinen vika 100 tunnissa on 8, siksi odotetaan 25 tunnissa neljännen osan vikoista, toisin sanoen 2 epäonnistumista. Tämä on parametri μ.

Epäonnistumisen 1 komponentin todennäköisyys pyydetään, satunnaismuuttuja on ”komponentit, jotka epäonnistuvat ennen 25 tuntia” ja sen arvo on y = 1. Korvaamalla todennäköisyysfunktio:

 b) Nyt satunnaismuuttuja on "komponentit, jotka epäonnistuvat ennen 50 tuntia". Parametri on μ = 4, Koska vikojen odotettu arvo 50 tunnissa on 4.

Kysymys on kuitenkin todennäköisyys, että alle kaksi komponenttia epäonnistuu 50 tunnissa, ei tarkalleen 2 komponenttia epäonnistuu 50 tunnissa, joten meidän on lisättävä todennäköisyydet, jotka:

-Kukaan ei epäonnistu

-Epäonnistuu vain 1

P (alle 2 komponenttia) = p (0) + p (1)

P (alle 2 komponenttia) = 0.0183+0.0732 = 0.0915

c) että vähintään 3 komponenttia epäonnistuu vuonna 125, se tarkoittaa, että 3, 4, 5 tai enemmän tuolloin voi epäonnistua.

Todennäköisyys, että esiintyy ainakin yksi monista tapahtumista, on yhtä suuri kuin 1, paitsi todennäköisyys, että mitään tapahtumista ei tapahdu.

-Pyydetty tapahtuma on epäonnistunut vähintään 3 komponenttia 125 tunnissa

-Että tapahtuma ei tapahdu, tarkoittaa, että alle 3 komponenttia epäonnistuu, jonka todennäköisyys on: P (0)+P (1)+P (2)

Jakauman μ -parametri on tässä tapauksessa:

 μ = 8 + 2 = 10 epäonnistumista 125 tunnissa.

P (langennut 3 tai useampaa komponenttia) = 1- P (0)- P (1)- P (2) =

= 1-0.0026786 = 0.9972

Viitteet

1. Matematiikka. Poisson -jakelu. Palautettu: on.Matematiikka.com
2. Mendenhall, W. 1981. Hallinnon ja taloustieteen tilastot. Kolmas. painos. Iberoamerica -toimitusryhmä.
3. Stat -vaellus. Opeta itsellesi tilastot. Poisson -jakelu. Palautettu: Statstrek.com,
4. Triola, m. 2012. Perustilastot. 11. päivä. Ed. Pearson -koulutus.
5. Wikipedia. Poisson -jakelu. Haettu: vuonna.Wikipedia.org