Poisson -kerroinkerroin, kaavat, arvot, esimerkit

Hän Poisson -kerroin Se on mitatton määrä, jokaiselle materiaalille ominainen määrä. Se osoittaa materiaalin muodonmuutosta ennen tiettyjä ponnisteluja.

Kun aineellinen kappale, joka läpikäy jännitystä tai puristusta, kärsii muodonmuutoksesta, poikittaisen muodonmuutoksen ja pitkittäisen muodonmuutoksen välinen osoitus on juuri Poisson -kerroin.

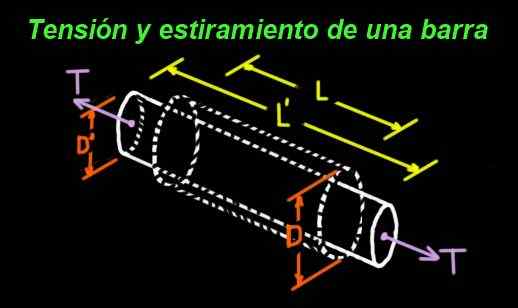
Kuvio 1. Poissonin kerroin mittaa pitkittäisen venytyksen ja poikittaisen kaventumisen välistä suhdetta. (Valmistaja Ricardo Pérez)

Esimerkiksi kumisylinteri, joka käy läpi jännityksen päissä. Kuvio 1 esittää palkin, jonka alkuperäiset mitat ovat: pitkä l ja halkaisija d.

Pylvälle altistetaan T -jännite sen päiden mukaan, ja tämän jännityksen seurauksena on venytys, niin että uusi pituus on L '> l. Mutta venyessään sen halkaisijan kaventuminen tapahtuu myös uuteen arvoon: D ' < D.

Venytys (positiivinen) ja kaventumisen (negatiivinen) välillä kerrotaan (-1) on positiivinen luku välillä 0-0,5. Tämä numero on niin kutsuttu Poisson ν -kerroin (kreikkalainen kirjain).

[TOC]

Poisson -kertoimen kaava

Poisson -kertoimen laskemiseksi on tarpeen määrittää pitkittäinen ja poikittainen yksikön muodonmuutos.

Pitkittäisen yksikön muodonmuutos ε_Lens Se on venytys jaettuna alkuperäisen pituuden kesken:

ε_Lens = (L ' - l) / l

Samoin poikittainen yhtenäinen muodonmuutos ε_T Se on säteittäinen kaventuminen jaettuna alkuperäisen halkaisijan kesken:

ε_T = (D ' - d) / d

Siksi Poisson -kerroin lasketaan seuraavalla kaavalla:

ν = - ε_T / ε_Lens 

Suhde joustavuusmoduuliin ja jäykkyysmoduuliin

Poisson ν -kerroin liittyy moduuliin JA joustavuus (tai nuori moduuli) ja jäykkyysmoduulilla G, seuraavan kaavan mukaan:

Voi palvella sinua: Geometrinen optiikka: Mitä tutkimuksia, lakeja, sovelluksia, harjoituksia

ν = E /(2G) - 1

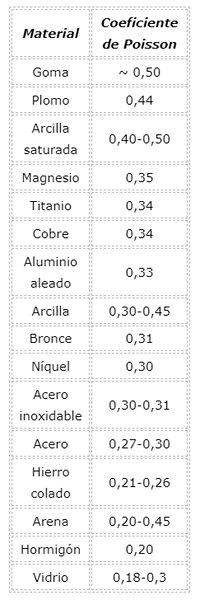
Poisson -kerroinarvo materiaaleille

Kuva 2. Ruostumattomasta teräksestä on Poisson -kerroin välillä 0,30 - 0,31. Lähde: Pixabay.

Esimerkkejä laskelmasta

Esimerkki 1

Tietyn muovimateriaalin palkin pituus on 150 mm ja halkaisijaltaan pyöreä leikkausleikkaus. Kun puristusvoima 612,25 kg-F: lle altistetaan puristusvoima, havaitaan 14 mm: n lyhenemistä ja samanaikaisesti palkin halkaisijan 0,85 mm: n nousu 0,85 mm.

Laskea:

a) Pitkittäinen yhtenäinen muodonmuutos.

b) poikittainen yhtenäinen muodonmuutos.

c) Poissonin materiaalin kerroin.

d) Nuorten joustavuusmoduuli, joka vastaa materiaalia.

e) kyseisen muovin jäykkyysmoduuli.

Liittää jhk

Muista, että pitkittäisen yksikön muodonmuutos εL on venytys jaettuna alkuperäisellä pituudella:

εl = (l ' - l) / l

εl = (-14 mm) / 150 mm = -0,0933

Huomaa, että pitkittäinen yhtenäinen muodonmuutos on ulottumaton, ja tässä tapauksessa se on antanut negatiivisen, koska sen pitkittäisulottuvuus laski.

Ratkaisu b

Samoin yhtenäinen poikittainen muodonmuutos εT on säteittäinen kaventuminen, jaettuna alkuperäisellä halkaisijalla:

εt = (d ' - d) / d

εt = (+0,85 mm) / 20 mm = 0,0425

Poikittainen yhtenäinen muodonmuutos on ollut positiivinen, koska palkin halkaisija on lisääntynyt.

Liuos C

Poisson -kertoimen laskemiseksi meidän on muistettava, että se on määritelty poikittaisen muodonmuutoksen ja pitkittäismuodon välisen osamäärän negatiiviseksi:

ν = - εt / εl 

ν = - 0,0425 / (-0,0933) = 0,4554

On muistettava, että Poissonin kerroin on positiivinen ulottumaton luku ja useimmille materiaaleille se on välillä 0 - 0,5.

Voi palvella sinua: Darcy Law

Liuos D

Youngin joustavuusmoduuli, joka on merkitty E -kirjaimella, on Hooken lain suhteellisuusvakio. E: n kautta normaali pyrkimys σL liittyy yhtenäiseen muodonmuutokseen εl, seuraavasti:

σl = e εl 

Normaali ponnistus määritellään normaalin voiman (tässä tapauksessa palkin akselin suuntainen) ja poikkileikkauksen välillä: poikkileikkauksen välillä: tässä tapauksessa:

σl = f / a = f / (π / 4 * d^2)

Tässä harjoituksessa voima F on 612,25 kg-F, joka tehdään Newtonille, joka on voimayksikkö:

F = 612,25 kg-f = 612,25 * 9,8 n = 6000 n = 6 kN

Poikkileikkaus A puolestaan ​​on:

A = (π/4 * d^2) = (3,1416/4) * (20 * 10^-3 m)^2 = 3,1416 * 10^-4 m^2

Viimeinkin palkkiin sovellettu normaali ponnistus on:

σl = f / a = 6000 N / 3,1416 * 10^-4 m^2 = 19.098.593 PA = 19 098 MPa

Youngin joustavuusmoduulin laskemiseksi puhdistamme ja Hooken laista σl = e εl:

E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPa

Ratkaisu E

R -jäykkyysmoduuli liittyy tämän kaavan avulla Youngin EG -moduuliin ja Poisson ν -kertoimeen:

E / (2 g) = 1 + ν 

Sieltä voit puhdistaa g:

G = e / (2 (1 + ν)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa

Esimerkki 2

Sinulla on 4 mm ja 1 m pitkä halkaisija kaapeli. Tietäen, että kuparin nuori moduuli on 110000 MPa ja.

Ratkaisu

Ensinnäkin on tarpeen laskea normaali vetoponnistus, jota paino käyttää johdolla tämän kaavan jälkeen:

Voi palvella sinua: Vektorit avaruudessa: Kuinka kuvaaja, sovellukset, harjoitukset

σl = f / a = f / (π / 4 * d^2)

Voima F on 980 N ja poikkileikkaus on:

A = (π/4 * d^2) = (3,1416/4) * (4 * 10^-3 m)^2 = 1,2566 * 10^-5 m^2

Sitten vetoponnistus on:

σl = 980 N / 1,2566 * 10^-5 m^2 = 77.986.000 PA

Yhtenäisen johdon muodonmuutoksen laskeminen

Youngin joustavuusmoduuli, joka on merkitty kirjaimella E

σl = e εl 

Sieltä kuparilangan pitkittäinen yhtenäinen muodonmuutos voidaan tyhjentää:

εl = σl / e = 77,986 MPa / 110000 MPa = 7,09 * 10^-4

Poikittaisen yhtenäisen muodonmuutoksen laskeminen

Toisaalta, tuntemaan poikittaisen yhtenäisen muodonmuutoksen, Poisson -kertoimet sovelletaan:

ν = - εt / εl 

Lopuksi, sinun on poikkeava yhtenäinen muodonmuutos on: 

εt = -ν εl = -0,34 * 7,09 * 10 ^-4 = -2,41 * 10 ^-4

Kaapelin absoluuttinen venytyslaskelma

Lopuksi, jotta voidaan tietää kaapelin absoluuttinen venytys, on käytettävä seuraavaa suhdetta:

Δl = εl * l = 7,09 * 10^-4 * 1 m = 7,09 * 10^-4 m = 0,709 mm

Eli tällä painolla kaapeli venyi tuskin 0,709 millimetriä.

Halkaisijan laskennan laskeminen

Absoluuttisen kutistumisen saamiseksi käytämme seuraavaa kaavaa:

Δd = εt * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0 000964 millimetriä.

Tämä halkaisijaltaan kapeneva on niin pieni, että on vaikea arvioida paljaalla silmällä, jopa sen mittaus vaatii suurta tarkkuuslaitetta.

Viitteet

1. Olut f ... materiaalimekaniikka. Viides. Painos. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Materiaalimekaniikka. Kahdeksas painos. Prentice Hall. 2011. 3-60.
3. Gere J. Materiaalimekaniikka. Kahdeksas painos. Cengage -oppiminen. 4-220.
4. Giancoli, D. 2006. Fysiikka: sovellusten periaatteet. 6. ed. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 87-98.