Lieriömäiset koordinaatit järjestelmä, muutos ja harjoitukset

Se lieriömäiset koordinaatit Ne palvelevat pisteitä kolmen ulottuvuuden tilassa ja koostuvat säteittäisestä koordinaatista ρ, atsimutaalinen koordinaatti φ ja korkeuskoordinaatti z -z.

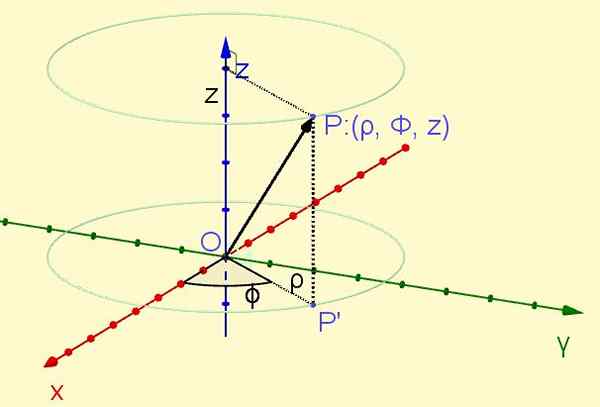
Piste P Avaruudessa sijaitseva on ortogonaalisesti lentokoneessa Xy aiheuttama P ' Siinä lentokoneessa. Etäisyys alkuperästä pisteeseen P ' määrittelee koordinaatti ρ, kun taas akselin muodostava kulma X Puoliksi Op ' Määritä koordinaatti φ. Lopuksi koordinaatti z -z Se on pisteen ortogonaalinen projektio P akselilla Z -z. (Katso kuva 1).

Kuvio 1. Sylinterimäisten koordinaattien piste P (ρ, φ, z). (Oma yksityiskohta)

Radiaalinen koordinaatti ρ on aina positiivinen, atsimutaalinen koordinaatti φ vaihtelee nollaradiaanista kahteen Pi Radianiin, kun taas Z -koordinaatti voi ottaa minkä tahansa todellisen arvon:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Koordinaattien muutos

Cartesian -koordinaattien (x, y, z) saaminen on suhteellisen helppoa pisteestä P lieriömäisistä koordinaateista (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Mutta on myös mahdollista saada polaariset koordinaatit (ρ, φ, z), joka perustuu pisteen P: n Cartesian -koordinaattien (x, y, z) tuntemiseen:

ρ = √ (x² + ja²-A

φ = arctan (y/x)

z = z

Vektoripohja lieriömäisissä koordinaateissa

Sylinterimäisten vektorien pohja on määritelty Uρ, Uφ, Uz.

Vektori Uρ Se on tangentti linjalle φ = cttte ja z = ctte (osoittaa säteittäisesti pois), vektori Uφ on tangentti linjalle ρ = cttte ja z = CTTE ja lopulta Uz Sillä on sama suunta Z -akselille.

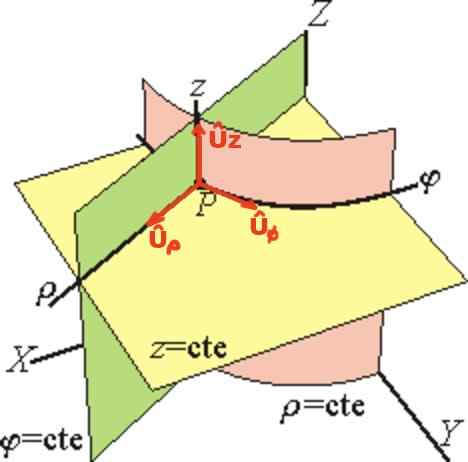Kuva 2. Lieriömäinen koordinaattipohja. (Wikimedia Commons)

Sylinterimäisen yksikön pohjassa sijaintivektori r - Kohdasta P on kirjoitettu veknisesti näin:

Se voi palvella sinua: funktion verkkotunnus ja ristiriita (esimerkkien kanssa)

r - = ρ Uρ + 0 - Uφ + z -z Uz

Toisaalta ääretön siirtymä Dr - Kohdasta P ilmaistaan ​​seuraavasti:

d -dr - = Dρ Uρ + ρ dφ  Uφ + Dz Uz

Samoin DV -tilavuuden ääretön elementti lieriömäisissä koordinaateissa on:

DV = ρ dρ Dz DZ

Esimerkit

On lukemattomia esimerkkejä lieriömäisten koordinaattien käytöstä ja soveltamisesta. Esimerkiksi kartografiassa lieriömäinen projektio, perustuu juuri näihin koordinaateihin. Esimerkkejä on enemmän:

Esimerkki 1

Sylinterimäisillä koordinaateilla on sovelluksia tekniikassa. Esimerkiksi sinulla on CHS (sylinterinpää-sektori) -järjestelmä datan sijaintipaikasta kiintolevyllä, joka todella koostuu useista levyistä:

- Sylinteri tai rata vastaa koordinaattia ρ.

- Sektori vastaa korkealla pyörivän albumin φ -sijaintia kulmanopeus.

- Pää vastaa vastaavan albumin lukupään Z -sijaintia.

Jokaisella tietotavulla on tarkka osoite lieriömäisissä koordinaateissa (C, S, H).

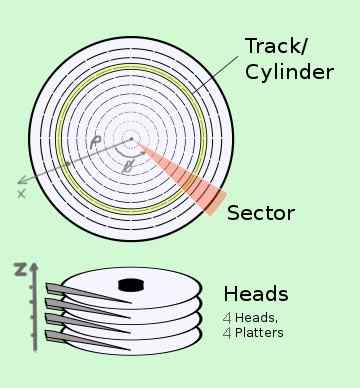Kuva 2. Tietojen sijainti lieriömäisissä koordinaateissa kiintolevyjärjestelmässä. (Wikimedia Commons)

Esimerkki 2

Rakennusnosturit asettavat kuormitusaseman lieriömäisissä koordinaateissa. Vaaka -asento määritellään etäisyydellä nosturille tai nuolelle. Kuorman pystysuuntainen sijainti määritetään korkeuden z -koordinaatin avulla.

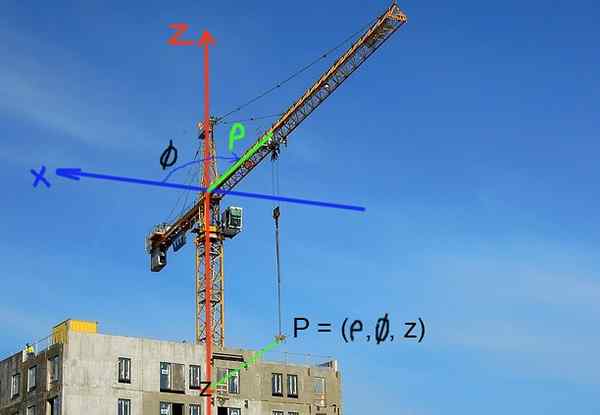Kuva 3. Kuorman sijainti rakennusnosturissa voidaan ilmaista helposti lieriömäisissä koordinaateissa. (Pixabay -kuva - RCOS R. Pérez)

Ratkaisut

Harjoitus 1

Sylinterimäisten koordinaattien (3, 120º, -4) ja sylinterimäisten koordinaattien piste P2 (2, 90º, 5) p1 -pisteitä on P1. Etsi Euklidian etäisyys Näiden kahden pisteen välillä.

Voi palvella sinua: Divisions, jossa jäännös on 300

Ratkaisu: Ensinnäkin etsimme jokaisen pisteen Cartesian koordinaatit edellä tapahtuvan kaavan jälkeen.

P1 = (3* cos 120º, 3* Sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

Euklidian etäisyys P1: n ja P2: n välillä on:

D (p1, p2) = √ ((0 - (-1.5))²+(2 - 2.60)²+(5 -(-4))² ) =…

… √ (2.25+0.36+81) = 9.14

Harjoitus 2

Pisteellä P on Cartesian koordinaatit (-3, 4, 2). Etsi vastaavat lieriömäiset koordinaatit.

Ratkaisu: Sylinterimäiset koordinaatit löytyvät käyttämällä yllä annettuja suhteita:

ρ = √ (x² + ja²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = Arcan (4/(-3)) = -53.13º + 180º = 126.87º

Z = 2

On muistettava, että kaarenkielinen funktio on jaksottavuuden monivaluada 180º. Lisäksi kulman φ on kuultava toiseen kvadranttiin, koska x e y ja pisteen P koordinaatit ovat siinä kvadrantissa. Tästä syystä tulokseen on lisätty 180º.

Harjoitus 3

Ilmaise sylinterimäisissä koordinaateissa ja karteesissa koordinoi radiosylinterin 2 pinnan ja jonka akseli on samanaikainen Z -akselin kanssa.

Ratkaisu: Ymmärretään, että sylinterillä on ääretön jatke Z -suuntaan, niin että mainitun pinnan yhtälö lieriömäisissä koordinaateissa on:

ρ = 2

Sylinterimäisen pinnan Cartesian yhtälön hankkimiseksi otetaan edellisen yhtälön molempien jäsenten neliö:

ρ² = 4

Kerrotaan yhdellä edellisen tasa -arvon molemmat jäsenillä ja soveltaa Perustavanlaatuinen trigonometrinen identiteetti (SEN²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(SEN²(φ) + cos²(φ)) * ρ² = 1 * 4

Suluista kehittyy:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Voi palvella sinua: väestö ja näyte

Muistamme, että ensimmäinen sulu (ρ SEN (φ)) on koordinaatti ja piste polaarikoordinaateissa, kun taas suluista (ρ cos (φ)) edustaa X -koordinaattia, joten olemme poistuneet Sylinteriyhtälö Cartesian koordinaateissa-

ja² + x² = 2²

Aikaisempaa yhtälöä ei pidä sekoittaa XY -tason ympyrän kanssa, koska tässä tapauksessa se olisi tämä: ja² + x² = 2² ; Z = 0.

Harjoitus 4

Sädesylinterin r = 1 m ja korkeus H = 1M: llä on säteittäisesti jakautunut massa seuraavan yhtälön D (ρ) = c (1 - ρ/r) mukaisesti, missä C on arvon vakio C = 1 kg/m³. Löydä sylinterin kokonaismassa kilogrammiksi.

Ratkaisu: Ensimmäinen asia on ymmärtää, että funktio D (ρ) edustaa tilavuusmallien tiheyttä ja että tiheysmassa jakautuu sylinterimäisiin kaskaroneihin keskustan tiheyden vähentämiseksi reuna -alueelle. Ääretön tilavuuselementti ongelman symmetrian mukaan on:

Dv = ρ dρ 2π h

Sieltä sinun täytyy, lieriömäisen kuoren ääretön massa on:

DM = D (ρ) DV

Joten sylinterin kokonaismassa ilmaistaan ​​seuraavalla Määritelty kiinteä-

M = ∫_jompikumpi^{R -} D (ρ) dv = ∫_jompikumpi^{R -} C (1 - ρ/r) ρ dρ 2π h = 2π h c ∫_jompikumpi^{R -} (1 - ρ/r) ρ dρ

Ilmoitetun integraalin ratkaisua ei ole vaikea saada, koska se on sen tulos:

∫_jompikumpi^{R -} (1 - ρ/r) ρ dρ = (⅙) r²

Tämän tuloksen sisällyttäminen sylinterimassan ilmentymiseen saadaan:

M = 2π h c (⅙) r² = ⅓ π h c r² =

 ⅓ π 1m*1kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Viitteet

1. Arfken G ja Weber H. (2012). Matemaattiset menetelmät fyysikoille. Kattava opas. 7. painos. Akateeminen lehdistö. ISBN 978-0-12-384654-9
2. CC -laskenta. Ratkaistu lieriömäinen ja pallomainen koordinaatit. Palautettu: laskelma.DC
3. Weisstein, Eric W. ”Sylinterimäiset koordinaatit.”Mathworld-a Wolfram -verkosta. Toipunut: MathWorld.Susi.com
4. Wikipedia. Lieriömäinen koordinaattijärjestelmä. Haettu: vuonna.Wikipedia.com
5. Wikipedia. Vektorikentät lieriömäisissä ja pallomaisissa koordinaateissa. Haettu: vuonna.Wikipedia.com