Pallomaiset koordinaatit esimerkit ja harjoitukset ratkaistu

Se pallomaiset koordinaatit Ne ovat pistepaikkajärjestelmä kolmen dimensionaalisessa tilassa, joka koostuu säteittäisestä koordinaatista ja kahdesta kulmakoordinaatista, joita kutsutaan polaarikoordinaattiksi ja atsimutaaliseksi koordinaatiksi.

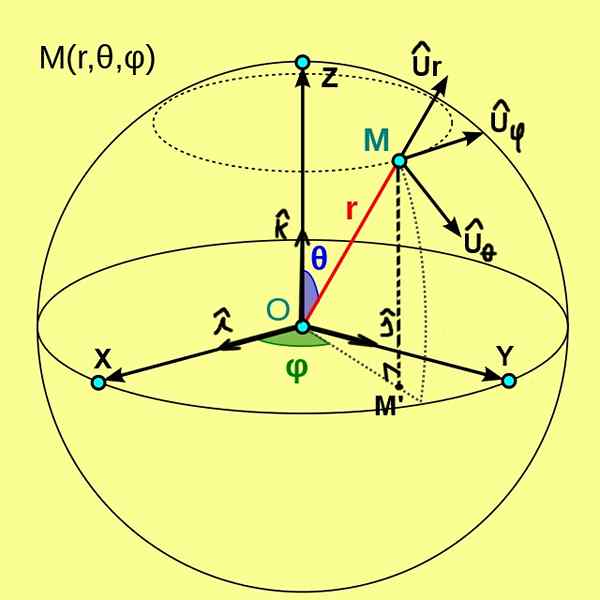
Kuviossa 1, jonka alla näemme, pisteen m pallomaiset koordinaatit (r, θ, φ) esitetään. Näihin koordinaateihin viitataan Cartesian akselien x, y, z ortogonaaliseen järjestelmään tai.

Kuvio 1. Pallomaiset koordinaatit (r, θ, φ) pisteestä m. (Wikimedia Commons)

Tässä tapauksessa pisteen M koordinaatti R on etäisyys siitä pisteestä alkuperään tai. Polaarikoordinaatti θ edustaa kulmaa positiivisen semi -akselin z: n ja vektorisäteen välillä OM. Vaikka atsimutaalinen koordinaatti φ on kulma positiivisen puoliakselin x ja vektorisäteen välillä ', koska M' on M: n ortogonaalinen projektio XY -tasolla.

Radiaalinen koordinaatti R ottaa vain positiivisia arvoja, mutta jos piste sijaitsee alkuperässä, niin r = 0. Polaarikoordinaatti θ ottaa vähimmäisarvona 0º positiivisessa puolijohdossa sijaitseville pisteille. Lopuksi, atsimutaalinen koordinaatti φ ottaa vähimmäisarvona 0º ja enimmäismäärän 360º.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

[TOC]

Koordinaattien muutos

Seuraavaksi annetaan kaavat, jotka sallivat pisteen m Cartesian koordinaatit (x, y, z) olettaen, että saman (r, θ, φ) pallomaiset koordinaatit: pisteen pallomaiset koordinaatit:

x = r Sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

z = r cos (θ)

Samoin on hyödyllistä löytää suhteet siirtyäkseen Cartesian koordinaateista (x, y, z) kyseisen pisteen pallomaisille koordinaateille annettavasta kohdasta:

R = √ (x^2 + y^2 + z^2)

θ = Arcan (√ (x^2 + y^2) / z)

Voi palvella sinua: Diskreetti satunnaismuuttuja

φ = arctan (y / x)

Vektoripohja pallomaisissa koordinaateissa

Pallomaisista koordinaateista määritetään perusvektoreiden ortonormal pohja, jonka merkitään Ur, Ur, Uφ. Kuvio 1 esittää nämä kolme yksikkövektoria, joilla on seuraavat ominaisuudet:

- Ur Se on säteittäiselle viivalle tangentti yksikkövektori θ = CTTE ja φ = CTTE;

- Ur Se on yksikön tangenttivektori kaariin φ = CTTE ja R = CTTE;

- Uφ Se on yhtenäinen vektori, joka on tangentti kaarille r = ctte ja θ = CTTE.

Linja- ja tilavuuselementit pallomaisissa koordinaateissa

Avaruuspisteen vektoriasento pallomaisissa koordinaateissa on kirjoitettu näin:

r - = r Ur

Mutta äärettömän pienen variaation tai siirtymisen pisteen kolmen dimensioisen tilan, näissä koordinaateissa se ilmaistaan ​​seuraavalla vektorisuhteella:

d -dr - = DR Ur + r dθ Ur + r sen (θ) dφ Uφ

Lopuksi, äärettömän määrän DV pallomaisissa koordinaateissa kirjoitetaan näin:

dv = r^2 sin (θ) dr dθ dφ

Nämä suhteet ovat erittäin hyödyllisiä linja -integraalien ja tilavuuden laskemisessa fyysisissä tilanteissa, joilla on pallomainen symmetria.

Suhde maantieteellisiin koordinaateihin

Maantieteelliset koordinaatit ymmärretään, että ne palvelevat paikkoja maan pinnalla. Tämä järjestelmä käyttää leveysasteen ja pituuden koordinaateja paikantaakseen asennon maan pinnalle.

Maantieteellisessä koordinaattijärjestelmässä maan pinnan oletetaan.

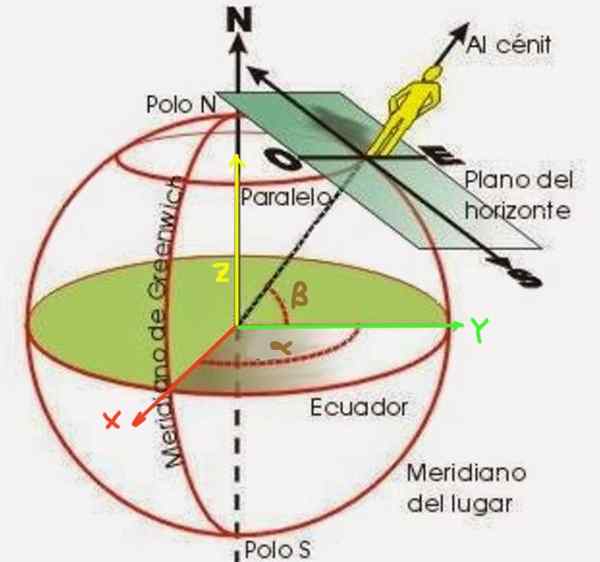Kuva 2. Tarkkailijan pituus α ja β leveysaste maan pinnalla.

Β -leveysaste on kulma, joka muodostuu sädeestä, joka alkaa maan keskustasta pisteeseen, jonka haluat sijoittaa. Se mitataan päiväntasaajan tasosta, kuten kuvassa 2 esitetään. Toisaalta pituus α on kulma, jonka pisteen meridiaani on muodossa nolla meridiaanille (tunnetaan nimellä Greenwich Meridian).

Voi palvella sinua: suhteellinen arvo

Leveysaste voi olla pohjoisen tai eteläisen leveysasteen mukaan riippuen siitä, onko paikallinen paikka pohjoisella pallonpuoliskolla vai eteläisellä pallonpuoliskolla. Samoin pituus voi olla länsi tai tämä riippuen siitä, onko sijainti länsi- tai itäpuolella nolla meridiaanista.

Kaavat muuttua maantieteellisestä pallomaiseksi

Näiden kaavojen saamiseksi ensimmäinen asia on luoda koordinaattijärjestelmä. XY -taso valitaan samaan aikaan päiväntasaajan tasolle, joka on positiivinen puoliakseli X, joka menee maan keskustasta ja nollameridianin läpi. Akseli puolestaan ​​ja kulkee 90º: n ja meridianin läpi. Maapallon pinnalla on RT -radio.

Tällä koordinaattijärjestelmällä on siten maantieteellinen pallomuutoksille:

αEβN → (RT, θ = 90º-β, φ = α)

αOβN → (RT, θ = 90º-β, φ = 360º-a)

αeβ → (RT, θ = 90º+β, φ = α)

αOβS → (RT, θ = 90º+β, φ = 360º-a) 

Esimerkit

Esimerkki 1

Palma de Mallorcan (Espanja) maantieteelliset koordinaatit ovat:

Itäpituus 38 847º ja pohjoinen leveysaste 39 570º. Palma de Mallorcaa vastaavien pallomaisten koordinaattien määrittämiseksi sovelletaan edellisen jakson kaavojen ensimmäisiä:

38 847ºE39,570ºN → (r = 6371 km, θ = 90º-39 570º, φ = 38 847º)

Sitten pallomaiset koordinaatit ovat:

Palma de Mallorca: (R = 6371 km, θ = 50,43º, φ = 38,85º)

Edellisessä vastauksessa R on otettu.

Esimerkki 2

Tietäen, että Falklandin saarilla (Falkland) on maantieteelliset koordinaatit 59ºO 51,75ºS, määritä vastaavat polaariset koordinaatit. Muista, että X -akseli menee maan keskustasta 0º meridiaaniin ja päiväntasaajan tasoon; Y -akseli myös päiväntasaajan tasossa ja 90º West Meridianin läpi; Lopuksi maanpäällisen kierto-akselin z-akseli eteläiseen suuntaan.

Voi palvella sinua: Curtory: Määritelmä, tyypit, kaavat, mitä se on esimerkiksi

Sitten löytääksesi vastaavat pallomaiset koordinaatit, käytämme edellisessä osassa esitettyjä kaavoja:

59ºO 51,75ºS → (r = 6371 km, θ = 90º+51,75º, φ = 360º-59º), toisin sanoen

Malvinat: (R = 6371 km, θ = 141,75º, φ = 301º)

Harjoitukset

Harjoitus 1

Löydä Palma de Mallorcan Cartesian koordinaatit Cartesiano XYZ -vertailujärjestelmästä, joka on esitetty kuvassa 2.

Ratkaisu: Aikaisemmin esimerkissä 1 saatiin pallomaiset koordinaatit Palma de Mallorcan maantieteellisten koordinaattien perusteella. Niin, että yllä esitetyt kaavat voidaan käyttää siirtymään pallomaisesta karteesialaisille:

x = 6371 km Sen (50,43º) cos (38,85º)

Y = 6371 km Sen (50,43º) Sen (38,85º) 

Z = 6371 km cos (50,43º)

Vastaavien laskelmien suorittaminen on:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Harjoitus 2

Löydä Falklandin saarten kartesian koordinaatit Cartesiano XYZ -vertailujärjestelmästä, joka on esitetty kuvassa 2.

Ratkaisu: Aikaisemmin esimerkissä 2 pallomaiset koordinaatit saatiin Falklandin saarten maantieteellisten koordinaattien perusteella. Niin, että yllä esitetyt kaavat voidaan käyttää siirtymään pallomaisesta karteesialaisille:

x = 6371 km Sen (141,75º) cos (301º)

y = 6371 km Sen (141,75º) Sen (301º) 

Z = 6371 km cos (141,75º)

Vastaavat laskelmat saadaan:

Falklandinsaaret: (x = 2031 km, y = -3381 km, z = -5003)

Viitteet

1. Arfken G ja Weber H. (2012). Matemaattiset menetelmät fyysikoille. Kattava opas. 7. painos. Akateeminen lehdistö. ISBN 978-0-12-384654-9
2. CC -laskenta. Ratkaistu lieriömäinen ja pallomainen koordinaatit. Palautettu: laskelma.DC
3. Tähtitieteen työpaja. Leveys-ja pituuspiiri. Haettu: korko.Blogin.com/
4. Weisstein, Eric W. ”Pallomaiset koordinaatit.”Mathworld-a Wolfram -verkosta. Toipunut: MathWorld.Susi.com
5. Wikipedia. Pallomainen koordinaattijärjestelmä. Haettu: vuonna.Wikipedia.com
6. Wikipedia. Vektorikentät lieriömäisissä ja pallomaisissa koordinaateissa. Haettu: vuonna.Wikipedia.com