Suorakulmaiset koordinaatit Esimerkit ja harjoitukset ratkaistu

Se suorakulmaiset koordinaatit o Cartesian ovat ne, jotka saadaan, kun heijastetaan ortogonaalisesti kolmessa Cartesian akselissa x, y, z piste, joka sijaitsee kolmen dimensioisessa tilassa.

Cartesian akselit ovat molemminpuolisesti kohtisuorassa suuntautuneita suoria. Cartesian -koordinaattijärjestelmässä kolme todellista numeroa, jotka ovat sen suorakaiteen muotoisia koordinaatit, on osoitettu jokaiselle avaruuden pisteelle.

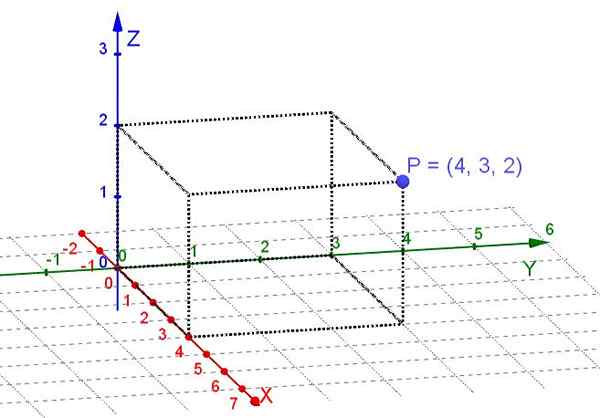
Kuvio 1. Pisteen P suorakulmaiset koordinaatit (oma yksityiskohta)

Kone on kolmen dimensionaalisen tilan alatila. Jos tason pisteitä harkitaan, riittää valitsemaan pari kohtisuora akselia x ja Cartesian järjestelmänä. Sitten hänelle osoitetaan kaksi todellista numeroa jokaisessa tasossa kaksi todellista numeroa, että hänen suorakaiteen muotoiset koordinaatit ovat.

[TOC]

Suorakulmaisten koordinaattien alkuperä

Ranskan matemaatikko René Descartes (1596 ja 1650) ehdottivat suorakaiteen muotoisia koordinaateja, minkä vuoksi he saavat kartesialaisten uskonnon.

Tällä descartes -ajatuksella tason ja avaruuden pisteille on osoitettu numerot siten, että geometriset luvut ovat liittyneet algebralliseen yhtälöön ja klassisiin geometrisiin lauseisiin voidaan osoittaa algebrallisesti. Cartesian koordinaattien kanssa syntyi analyyttinen geometria.

Cartesian lentokone

Jos valitaan tasolla kaksi kohtisuoraa viivaa, jotka leikkaavat yhdessä pisteessä tai; Ja jos jokaiselle riville on annettu suunta ja numeerinen asteikko peräkkäisten yhtäläisten pisteiden välillä, on silloin Cartesian järjestelmä tai suunnitelma, jossa jokainen tason piste liittyy järjestettyyn pariin kahdesta todellisesta numerosta, jotka ovat sen projektioita X- ja Y -akselit.

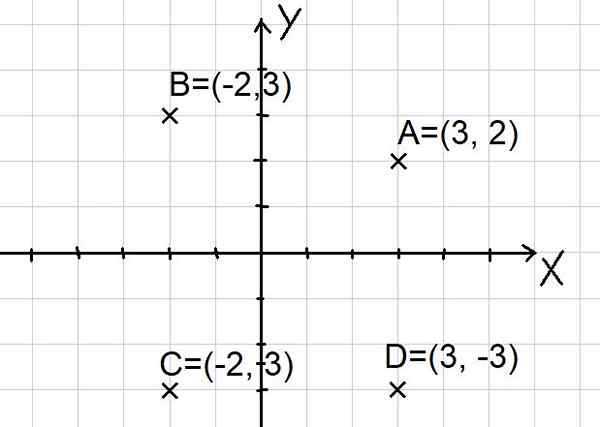
Pisteet a = (3, 2); B = (-2, 3); C = (-2, -3) ja d = (3, -3) on esitetty Cartesian -tasossa alla esitetyllä tavalla:

Kuva 2. Pisteitä Cartesian lentokoneessa. (Oma yksityiskohta)

Huomaa, että kaksi x- ja y -akselia jakavat taso neljään sektoriin, joita kutsutaan kvadranteiksi. Kohta A on ensimmäisessä kvadrantissa, toisessa kvadrantin B, C: n kolmannessa kvadrantissa ja pisteessä D neljännessä kvadrantissa.

Voi palvella sinua: väestö ja näyte

Kahden pisteen välinen etäisyys

Kartesian tason kahden pisteen A ja B välinen etäisyys on niiden yhdistävän segmentin pituus. Tämä etäisyys voidaan laskea analyyttisesti seuraavasti:

D (a, b) = √ (bx - ax)^2 + (by - ay)^2)

Etukaava saadaan soveltamalla Pythagoras -lause.

Mainitun kaavan soveltaminen kuvion 2 pisteisiin A, B on:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Toisin sanoen d (a, b) = 5,10 yksikköä. Huomaa, että etäisyys saatiin ilman tarvetta mitata säännöllä, on noudatettu täysin algebrallista menettelyä.

Linjan analyyttinen ekspressio

Suorakulmaiset koordinaatit mahdollistavat geometristen objektien, kuten pisteen ja linjan, analyyttisen esityksen. Kaksi pistettä A ja B määrittelevät yhden rivin. Linjan kaltevuus on määritelty osamääräksi koordinaattien ja pisteen B välillä vähemmän, jaettuna pisteen B X -koordinaattien erolla

vireillä = (by - ay)/(bx - kirves)

Minkä tahansa koordinaattien (x, y) pisteellä, joka kuuluu linjalle (AB), on oltava sama kaltevuus:

vireillä = (y - ay)/(x - kirves)

Yhtälö, joka saadaan rinteiden tasa -arvolla, on pisteiden A ja B läpi kulkevan linjan analyyttinen tai algebrallinen esitys:

(y - ay)/(x - ax) = (by - ay)/(bx - ax).

Jos sinut otetaan A ja B, kuvan 2 suorakulmaiset koordinaatit ovat:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

Tässä nimenomaisessa tapauksessa on linja negatiivisella kaltevuudella -⅕, mikä tarkoittaa, että linjapisteessä sijaitseva ja X -koordinaatin lisääminen yksikössä, koordinaatti ja laskee 0,2 yksikössä. 

Voi palvella sinua: Toroid tai Toro Dona

Tavallisin tapa kirjoittaa viivan yhtälö tasoon on koordinaatti ja selkeä muuttujan x funktiona:

y = -(1/5) x + 13/5 

Esimerkit

Esimerkki 1

Hanki analyyttisillä menetelmillä pisteiden C ja A välinen etäisyys, joka on C = (-2, -3) suorakulmaiset koordinaatit ja a = (3.2) koordinaatit.

Näiden kahden pisteen välisen euklidisen etäisyyden kaava on kirjoitettu näin:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Korvaamalla sen vastaavat suorakulmaiset koordinaatit:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7,07

Esimerkki 2

Hanki viivan yhtälö, joka kulkee koordinaattien (-2, -3) ja koordinaatin pisteen C läpi kulkevan pisteen C läpi (2, 0).

Ensinnäkin saadaan CP -viivan kaltevuus:

vireillä = (0 -(-3)) / (2 -( -2)) = ¾ 

Minkä tahansa pisteen Q yleisen suorakulmaisen koordinaatin (x, y), joka kuuluu CP -linjaan, on oltava sama kaltevuus:

vireillä = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Toisin sanoen CP -viivan yhtälö on:

(Y +3) / (x +2) = ¾

Vaihtoehtoinen tapa kirjoittaa CP -rivin yhtälö on puhdistaminen ja:

y = ¾ x - 3/2 

Ratkaisut

Harjoitus 1

Hanki risteyspisteen suorakulmaiset koordinaatit linjojen y = - (1/5) x + 13/5 ja linjan y = ¾ x - 3/2 välillä.

Ratkaisu: Määritelmän mukaan kahden viivan leikkauspiste on samat suorakaiteen muotoiset koordinaatit. Siksi koordinaatit ja risteyspisteessä on identtinen molemmille linjoille:

-(1/5) x + 13/5 = ¾ x - 3/2

Mikä johtaa seuraavaan ilmaisuun:

Voi palvella sinua: suorakulmio Trapezoid: Ominaisuudet, suhteet ja kaavat, esimerkit

(¾ + ⅕) x = 13/5 +3/2

Fraktioiden summan ratkaiseminen saadaan:

19/20 x = 41/10

Selvä x:

x = 82/19 = 4,32

Arvon ja risteyksen saamiseksi yhdestä viivasta saatu X -arvo korvataan:

y = ¾ 4,32 - 3/2 = 1,74

Tämä tarkoittaa, että annetut viivat sieppataan koordinaattien I = (4,32; 1,74) pisteessä I I = (4,32; 1,74).

Harjoitus 2

Hanki ympärysyhtälö, joka kulkee suorakaiteen muotoisen koordinaattipisteen R (3, 4) läpi ja jolla on keskus koordinaattien alkuperästä.

Ratkaisu: Radio R on etäisyys pisteestä r alkuperään tai koordinaateihin (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Eli se on säde 5 ympyrä 5, joka on keskitetty (0,0).

Jokaisella kehän pisteen P (x, y) on oltava sama etäisyys 5 keskustaan ​​(0, 0), mitä voidaan kirjoittaa:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Tarkoittaen:

√ (x^2 + y^2) = 5

Neliöjuuren poistamiseksi molemmat tasa -arvon jäsenet jätetään hiljaa:

x^2 + y^2 = 25

Mikä on kehäyhtälö.

Tällä esimerkillä on havainnollistettu suorakaiteen muotoisen koordinaattijärjestelmän voima, joka mahdollistaa geometristen esineiden, kuten kehän, määrittämisen ilman tarvetta käyttää paperia, lyijykynää ja kompassia. Vain algebrallisilla menetelmillä pyydetty ympärysmitta on määritetty.

Viitteet

1. Arfken G ja Weber H. (2012). Matemaattiset menetelmät fyysikoille. Kattava opas. 7. painos. Akateeminen lehdistö. ISBN 978-0-12-384654-9
2. CC -laskenta. Suorakaiteen muotoiset koordinaatit ratkaistu ongelmat. Palautettu: laskelma.DC
3. Weisstein, Eric W. ”Cartesian koordinaatit.”Mathworld-a Wolfram -verkosta. Toipunut: MathWorld.Susi.com
4. Wikipedia. Cartesian koordinaattijärjestelmä. Haettu: vuonna.Wikipedia.com