Yhtenäisen ympyrän trigonometriset toiminnot ja sovellukset

Hän Yhtenäisympyrä Se on sädeympyrä, joka on yhtä suuri kuin 1, joka on yleensä keskittynyt Cartesian -koordinaattijärjestelmän pisteeseen (0,0) Xy. Sitä käytetään helposti määrittelemään kulmien trigonometriset syyt suorakulmioilla.

Alkuperäiseen keskittyvä yhtenäinen ympyrän yhtälö on:

x² + ja² = 1

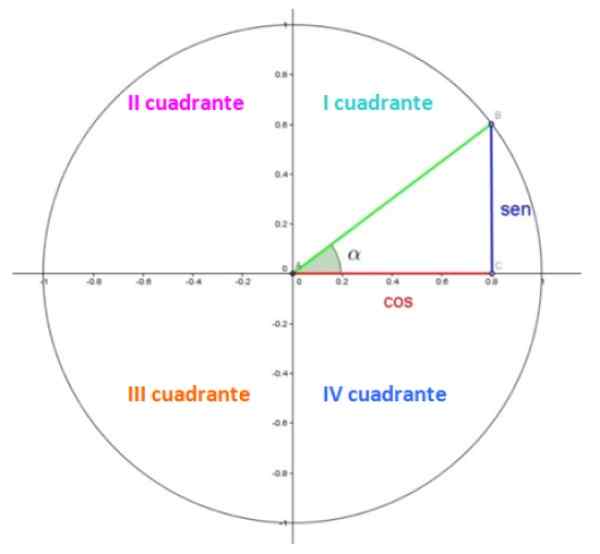
Kuvio 1. Yksikköympyrä. Lähde: Wikimedia Commons.

Kuvassa 1 meillä on yksikköympyrä, jossa jokainen huone on kvadrantissa. Quadrantit on numeroitu roomalaisilla numeroilla ja lasketaan anti -Horary.

Ensimmäisessä kvadrantissa on kolmio. Luokat, punaisella ja sinisellä mittauksella 0.8 ja 0.6, vaikka hypotenuse vihreissä mittoissa 1, koska se on radio.

Akuutti kulma α on keskikulma tavanomaisessa asennossa, mikä tarkoittaa, että sen kärki on samanaikainen piste (0,0) ja sen alkupuolella positiivisen X -akselin kanssa. Kulma mitataan kellon kädet vastoin, ja yleissopimuksella on positiivinen merkki.

No, yksikköympyrässä, kosenon koordinaatit ja α sini ovat vastaavasti pisteen B X- ja Y -koordinaatit, jotka esitetyssä esimerkissä ovat 0.8 ja 0.6.

Näistä kahdesta ne on määritelty:

• TG α = sin α/cos α = 0.6/0.8 = 0.75
• SEC α = 1/ cos α = 1/0.8 = 1.25
• haittaa α = 1 / sin α = 1/0.6 = 1.66 ..
• ctg α = 1/tg = 0.8/0.6 = 1.33 ..

[TOC]

Yhtenäiset ympyrän sovellukset

Jos rajoitamme itsemme suorakulmioihin, trigonometrisiä syitä sovellettaisiin vain akuutihin kulmiin. Yksikön ympyrän avulla trigonometriset syyt kuitenkin laajennetaan mihin tahansa kulmaan α.

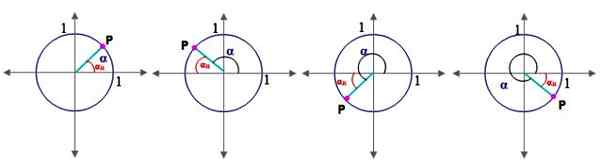Kuva 2.- Kulmat kvadranteissa ja viitekulma yksikköympyrässä. Lähde: f. Zapata.

Tätä varten on ensin määritettävä referenssikulman α käsite α_{R -}-

Voi palvella sinua: äärellinen sarja: Ominaisuudet, esimerkit, ratkaisut harjoitukset

Viitekulma

Olkoon α kulma vakioasennossa (joka on Alku samaan aikaan positiivisen X -akselin kanssa), sen referenssikulma α_{R -} Se on sen joukossa terminaalipuoli ja X -akseli. Kuvio 2 näyttää kulman kulman I, II, III ja IV kvadrantissa.

Jokaiselle kvadrantille referenssikulma lasketaan seuraavasti:

-Ensimmäinen kvadrantti: α_{R -} = α

-Toinen kvadrantti: α_{R -} = 180º - α

-Kolmas kvadrantti: α_{R -} = α - 180º

-Neljäs kvadrantti: α_{R -} = 360º - α

Huomaa, että ensimmäinen kvadranttikulma α osuu sen referenssikulmaan. No, kulman α trigonometriset syyt ovat samat kuin niiden referenssikulma, merkkejä niiden mukaan, joilla on kvadrantit, joissa α: n pääteosa putoaa.

Toisin sanoen, trigonometriset syyt Coseno ja Kulman α rinta vastaavat pisteen P koordinaattien kanssa, kuvan 2 mukaan.

Seuraavassa kuvassa näemme joidenkin merkittävien kulmien trigonometriset syyt, kuten yksikköympyrästä johdetaan.

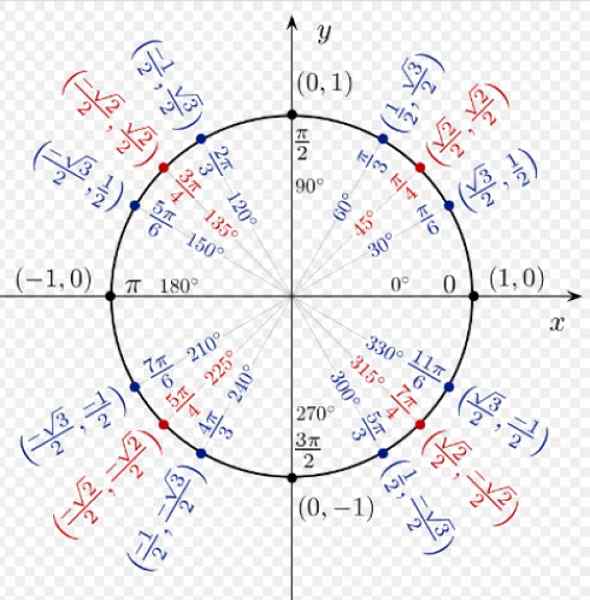Kuva 3. Joidenkin merkittävien pisteiden koordinaatit yksikköympyrässä. Lähde: Wikimedia Commons.

Syyt Coseno ja Rinta minkä tahansa I -kvadrantin kulman rinnassa ovat kaikki positiivisia. Α = 60º meillä on koordinaatit (1/2; √3/2), jotka vastaavat vastaavasti COS 60º: een ja SEN 60º: een.

Α = 120º: n koordinaatit ovat (-1/2; √3/2), koska toisessa kvadrantissa X-koordinaatti on negatiivinen.

Kosinin ja sinuksen kaavioiden asettelu

Yksikön ympyrän ja siinä olevien pisteiden koordinaatit on mahdollista piirtää funktioiden kaaviot cos t ja sen t, kuten alla näemme.

Voi palvella sinua: Kulma siirtymä

Tätä varten useita pistep (t) -asentoja sijaitsee yksikköympyrässä. Aloitamme funktion f (t) = sen t -kaaviolla.

Voimme havaita, että kun siirrymme T = 0: sta t = π/2 (90º), sen t -arvo nousee arvoon 1, mikä on maksimiarvo.

Toisaalta, välillä t = π/2 -t = 3π/2, sin T: n arvo laskee 1: stä, kulkee 0: n läpi t = π sen minimiin -1: llä t = 3π/2: lla.

Kuvio näyttää F (t) = sentin ensimmäisen syklin kaavion, joka vastaa ensimmäistä paluuta yksikköympyrään, tämä toiminto on jaksollinen jakso 2π.

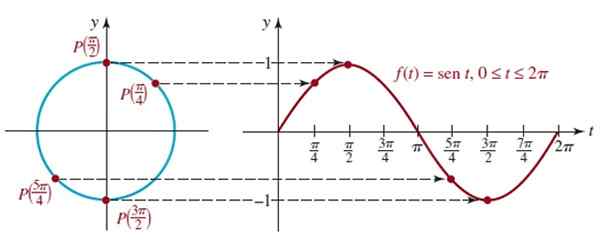Kuva 4. F (t) -kaavion kuva = sens sykli. Lähde: Zill, D. Algebra, trigonometria ja analyyttinen geometria.

Analoginen menettely voidaan suorittaa funktion f (t) = cos t -kaavion saamiseksi seuraavassa animaatiossa:

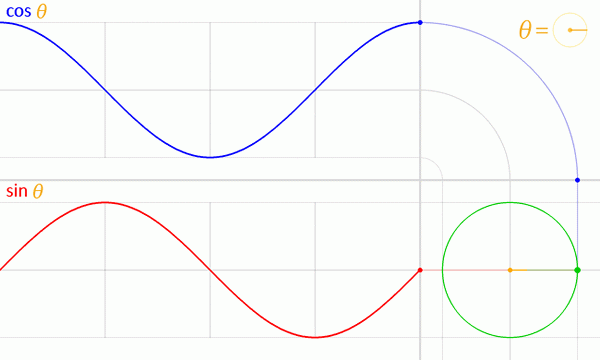Kuva 5. Kaaviot sini- ja kosinifunktioista yksikköympyrästä. Lähde: Wikimedia Commons.

Seno- ja Coseno -funktio -ominaisuudet

-Molemmat toiminnot ovat jatkuvia todellisten ja myös jaksollisten lukujen, ajan 2π.

-Funktioiden alue f (t) = sen t ja f (t) = cos t ovat kaikki todellisia lukuja: (-∞, ∞).

-Rinta- tai sinus- ja kosinireitille sinulla on aikaväli [-1,1]. Suluet osoittavat, että -1 ja 1 ovat mukana.

- Sin T Zerot ovat arvoja, jotka vastaavat Nπ: tä n kokonaisluvun kanssa, kun taas cos t: n nollat ​​ovat [(2n+1)/2] n myös kokonaisia.

-Funktio f (t) = sin t on outo, sillä on symmetria alkuperän suhteen, kun taas cos t -toiminto on tasainen, sen symmetria on suhteessa pystysuoraan akseliin.

Voi palvella sinua: Satunnaiset valinnat korvaavan tai ilman

Ratkaisut

- Harjoitus 1

Annetaan cos t = - 2/5, joka on pisteen p (t) vaakakoordinaatti yksikköympyrässä toisessa kvadrantissa, hanki vastaava pystysuuntainen koordinaatti sentin t.

Ratkaisu

Koska p (t) kuuluu yksikköympyrään, jossa se on täytetty, että:

x² + ja² = 1

Siksi:

y = ± √ 1 - x²

Koska p (t) on toisessa kvadrantissa, positiivinen arvo otetaan. Pisteen P (t) pystysuuntainen koordinaatti on y:

y = √ 1 - (-2/5)² = √0.84

- Harjoitus 2

Matemaattinen malli lämpötilaan T Asteina Fahrenheit joka päivä, t Tuntia keskiyön jälkeen se antaa:

T (t) = 50 + 10 sen [(π /12) × (t - 8)]

T: n kanssa ymmärretään 0–24 tuntia. Löytö:

a) lämpötila kello 8.00.

b) tunteja, joiden aikana t (t) = 60 ºF

c) Maksimin ja minimaaliset lämpötilat.

Liittää jhk

Korvaamme t = 8 annetussa toiminnossa:

T (8) = 50 + 10 sen [(π/12) × (t-8)] = 50 + 10 Sen [(π/12) × (8-8)] =

= 50 + 10 x Sen 0 = 50 ºF

Ratkaisu b

50 + 10 Sen [(π/12) × (T-8)] = 60

Se on trigonometrinen yhtälö ja sinun on puhdistettava tuntematon "T":

10 Sen [(π/12) × (t -8)] = 60 - 50 = 10

sin [(π/12) × (t-8)] = 1

Tiedämme, että sen π/2 = 1, siksi rintojen argumentin on oltava 1:

(π/12) × (t-8) = π/2

T-8 = 6

t = 14 h

Johtopäätöksenä on, että 14 tuntia keskiyön jälkeen lämpötila on 60 °, ts. 14 pm. Koko päivän (24 tuntia) ei ole muuta tuntia, jossa tämä tapahtuu.

Liuos C

Maksimilämpötila vastaa arvoa, jossa SEN [(π/12) × (T-8)] = 1 ja on 60 ºF. Toisaalta vähimmäismäärä tapahtuu, jos sen [(π/12) × (t -8)] = -1 ja on 40 ºF.

Viitteet

1. Figuera, J. 1999. Matematiikka. Ensimmäinen. Monipuolinen. Bolivarian kollegiaaliset versiot.
2. Hoffman, J. Matematiikan aiheiden valinta. Osa 4.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Matematiikka on hauskaa. Yksikköpiiri. Toipunut: MathSisfun.com.
5. Wikipedia. Trigonometrian identiteetit ja kaavat. Palautettu: on.Wikipedia.org.
6. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.