Trigonometrinen identiteetti (esimerkit ja harjoitukset)

Se trigonometrinen identiteetti Nämä ovat trigonometristen syiden välisiä suhteita, jotka ovat totta muuttujan arvoon. Esimerkiksi:

Tan θ = sin θ /cos θ

Se on trigonometrinen identiteetti, joka liittyy kulmaan θ, tangentti, rinta ja mainittu kulman kosiini kolme syytä.

Kuvio 1. Jotkut trigonometriset identiteetit, joita käytetään laajasti laskelmassa. Lähde: f. Zapata.

Tämä identiteetti on totta kaikelle arvolle, paitsi ne, jotka tekevät 0 nimittäjästä. Cos θ on 0 θ = ± π/2, ± 3π/2, ± 5π/2… Toinen esimerkki trigonometrisesta identiteetistä on:

sin x . Sekoitus . Ctg x = 1

[TOC]

Esittely

On olemassa kaksi perustapaa osoittaa, että trigonometrinen identiteetti on totta:

1- Yhden tasa-arvon jäsenten muuttaminen toiseksi kätevien algebrallisten manipulaatioiden avulla.

2- Kehitä molempia tasa-arvojäseniä erikseen, kunnes kunkin vastaavat lopulliset lausekkeet ovat täsmälleen samat.

Ehdotetussa identiteetissä aiomme muuttaa tasa -arvon vasemman puolen, jolle ilmaisemme CTG X: n ja SEC X: n rintojen ja kosinin suhteen seuraavasti:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Korvaamme tämän lausekkeen identiteetin vasemmalla puolella ja yksinkertaistamme:

sin x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

Ja identiteetin todenmukaisuus on jo todistettu.

Trigonometristen identiteettien tyypit

Trigonometrisiä identiteettejä on monenlaisia. Seuraavaksi kuvaamme lyhyesti tärkeimmät:

- Perustavanlaatuiset trigonometriset identiteetit

Erotamme kaksi tyyppisiä perus- identiteettejä:

I) Ne, jotka ilmaistaan ​​perussyistä, kosiini ja tangentti:

• Sec x = 1 /cos x
• Haittaa x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) pariteetista johdetut. Tiedämme sen kaavion kautta, että Sen X on pariton funktio, mikä tarkoittaa sitä:

Voi palvella sinua: 60 jakajaa

sin (-x) = - sin x

Siksi Cos X on pari, siksi:

cos (-x) = cos x

Niin:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Samalla lailla:

• cotg (-x) = -ctg x
• Sec (-x) = sek x
• haittaa (-x) = - haittaa x

- Pythagorean -identiteetti

Ne ovat niitä, jotka on saatu Pythagoras -lauseen levittämisestä kissojen A ja B ja Hypotenusa C: n suorakulmiokolmioon. Katsotaan:

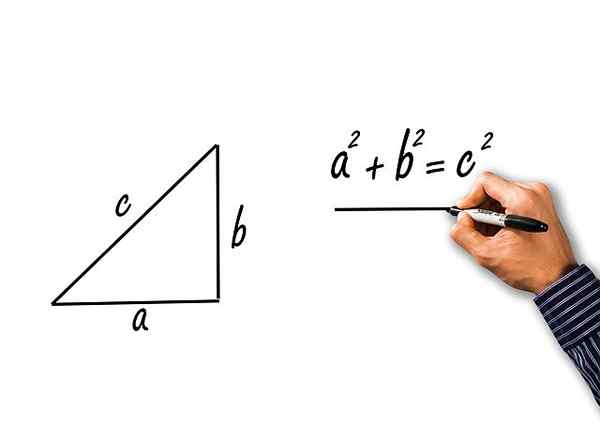Kuva 2.- Pythagoras -lauseesta saadaan kolme Pythagoran trigonometristä identiteettiä. Lähde: Pixabay.

Pythagoras -lause toteaa, että:

c² = a² + b -²

Jakamalla kaikki c: n välillä²-

c² / c² = (a² / c²) + (B² / c²-A

Vasemmalla puolella oleva termi on 1 ja muistaa, että akuutin kulman α sinus ja kosiini on määritelty seuraavasti:

sin α = a/c

cos α = b/c

Tulos:

1 = (sin α)² + (cos α)²

Tämä identiteetti tunnetaan nimellä perustavanlaatuinen identiteetti.

Menettely voidaan suorittaa jakamalla² ja b², mikä aiheuttaa vielä kaksi identiteettiä:

Sekoitus² α = 1 + TG² α

harja² α = 1 + CTG² α

- Kosinin ja rinnan kaavat kulmien summa/vähennys

Seuraavat ovat tärkeimmät trigonometriset identiteetit summan ja vähennysten kosinun, rintojen ja tangenttien kanssa:

SEN -demonstraatio (a + β) ja cos (α + β)

Nämä identiteetit voidaan osoittaa geometrisesti tai myös Euler -kaavan kautta:

ja^Ia = cos α + i sin α

Katsotaanpa mitä kaavalle tapahtuu, kun korvataan kahden kulman α ja β: n summa:

ja^{I (α +β-A} = cos (α + β) + i sin (α + β)

Tämä ekspressio on monimutkainen, sen todellinen osa on cos (α + β) ja sen kuvitteellinen osa on I Sin (α + β). Pidämme tätä tulosta käyttää sitä myöhemmin ja keskitymme eksponentiaalisen osan kehittämiseen:

ja^{I (α +β-A} = e^Ia ⋅ e^Ip = (cos α + i sin α) . (cos β + i sin β) =

Voi palvella sinua: kuusikulmainen prisma

= cos α⋅cos β + cos α⋅i SEN β + I⋅sen α cos β - SEN α⋅SEN β

Tämän lausekkeen todellinen osa on se, jota ei kerrota kuvitteellisella yksiköllä "I":

cos α⋅cos β - SEN α. SEN β

Siksi kuvitteellinen osa on:

I (cos ⋅sen β + sen α⋅cos β)

Jotta kaksi monimutkaista lauseketta olisivat samat, yhden todellisen osan on oltava yhtä suuri kuin toisen todellinen osa. Sama koskee kuvitteellisia osia.

Otamme tuloksen tallennettuna ja vertaamme sitä tähän:

cos α. cos β - Sen α. sin β = cos (α + β)

I (cos α⋅sen β + SEN α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. SIN β + SEN α⋅COS β)

- Kaksoiskulman kaavat

Edellisissä kaavoissa otamme β = α ja kehitämme:

sin (α + α) = SEN 2 α = SEN α⋅COS α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - Sen α⋅sen α = cos² α - Sen ² α

TG (α + α) = TG 2 α = [TG α + TG α] / [1-TG α⋅TG α] = 2TG α / 1-TG² α

Jos toisessa lausekkeessa korvataan² α = 1 - Sen² α saadaan:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Puolikangas kaavat

Tässä viimeisessä ekspressiossa korvaamme α α/2: lla, seuraava jäljellä on:

cos α = 2 cos ²(α/2) -1

Selvitä:

Ratkaisut

- Harjoitus 1

Näytä se:

Ratkaisu

Aiomme työskennellä algebrallisesti termin vasemmalle niin, että se näyttää oikealta. Kuten oikealla termillä näyttää sen x, ensimmäinen askel on ilmaista cos²X Sen X: n suhteen niin, että kaikki on saman trigonometrisen syyn suhteen:

Se voi palvella sinua: fraktio vastaa 3/5 (ratkaisu ja selitys)

Sitten 1 - Sen on tekijä² x täydellisten neliöiden erotuksena. Tätä varten se puhdistuu perustavanlaatuisesta identiteetistä:

koos²X = 1 - Sen² x

1 - Sen² x = (1- sin x) (1+senx)

Ja alkuperäisen lausekkeen tekijä on korvattu:

Termi (1- SENX) yksinkertaistetaan ja tasa-arvo säilyy:

1 + Sen x = 1 + senx

- Harjoitus 2

Ratkaise seuraava trigonometrinen yhtälö ja anna ratkaisu arvoille välillä 0 - 360º:

Tg x + s² x = 3

Ratkaisu

Vasemman ajan on olemassa kaksi trigonometristä syytä, joten sinun on vähennettävä kaikki yhdeksi, jotta voidaan puhdistaa tuntematon. Termi sekunti² X ilmaistaan ​​yhden Pythagorean -identiteetin kautta:

Sekoitus² α = 1 + TG² α

Korvaamalla yhtälö:

Tg x + 1 + tg² x = 3

Termien järjestäminen:

Tg² x + tg x + 1 = 3

Tämä yhtälö ratkaistaan ​​muuttamalla muuttujaa:

tg x = u

tai² + U + 1 - 3 = 0 → U² + U - 2 = 0

Tämä toisen asteen yhtälö ratkaistaan ​​helposti tekijällä:

(U +2) (U-1) = 0

Siksi u₁ = -2 ja u₂ = 1, vastaa:

TG X₁ = -2

TG X₂ = 1

Lopuksi:

x₁ = arctg (-2) = 296.Kuudes

x₂  = Arctg (1) = 45º

Viitteet

1. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
2. Figuera, J. 1999. Matematiikka. Ensimmäinen. Monipuolinen. Bolivarian kollegiaaliset versiot.
3. Hoffman, J. Matematiikan aiheiden valinta. Osa 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Trigonometrian identiteetit ja kaavat. Palautettu: on.Wikipedia.org.
6. Zapata, f. 4 tapaa ratkaista toisen asteen yhtälö. Toipunut: Francesphysics.Blogin.com.
7. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.