Mitkä ovat Cartesian lentokoneen osat?
- 3677
- 367
- Alonzo Kirlin
Se Cartesian lentokoneen osat Ne koostuvat kahdesta todellisesta, kohtisuorasta viivasta, jotka jakavat Cartesian -tason neljään alueeseen. Jokaista näistä alueista kutsutaan kvadrantsiksi ja Cartesian lentokoneen elementtejä kutsutaan pisteiksi. Tasoa yhdessä koordinaattiakselien kanssa kutsutaan Karteesilentokone Ranskan filosofin René Descartesin kunniaksi, joka keksi analyyttisen geometrian.
Kaksi viivaa (tai koordinaattiakselia) ovat kohtisuorassa, koska ne muodostavat 90º kulman niiden välillä ja ristivät yhteiseen pisteeseen (alkuperä). Yksi viivoista on vaakasuora, jota kutsutaan X: n (tai abcisa) alkuperästä ja toinen viiva on pystysuora, sitä kutsutaan y: n alkuperästä (tai tilattu).
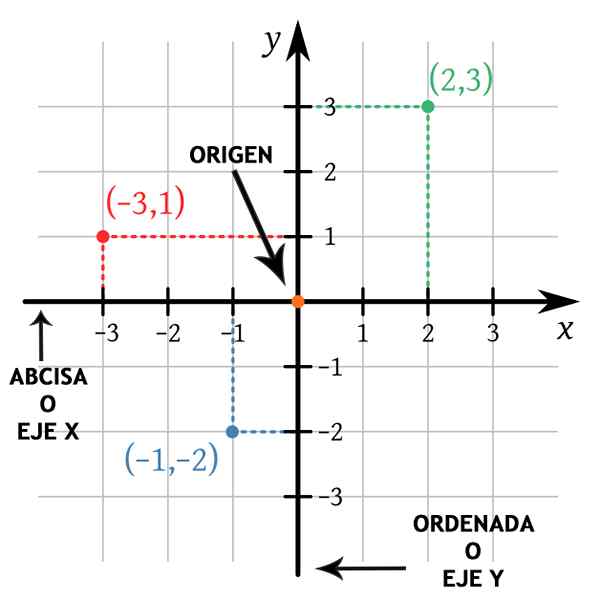 Kbolino / julkinen alue
Kbolino / julkinen alue X -akselin positiivinen puoli on alkuperän oikealla puolella ja Y -akselin positiivinen puoli on alkuperästä. Tämä mahdollistaa Cartesian -tason neljän neljänneksen erottamisen, mikä on erittäin hyödyllistä, kun koristavat pisteitä koneeseen.
Cartesian lentokoneet
Jokaisessa vaiheessa P Lentokoneeseen voidaan antaa pari reaalinumeroa, jotka ovat sen Cartesian koordinaatit.
Jos vaakasuora viiva ja pystysuora viiva käyvät läpi P, Ja leikkaat x: n ja akselin kohdalla Y -akseliin -lla ja b - vastaavasti, sitten koordinaatit P ovat (-lla,b --A. Sitä kutsutaan (-lla,b -) Järjestetty pari ja järjestys, jossa numerot kirjoitetaan.
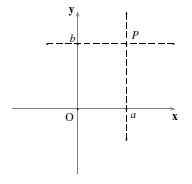
Ensimmäinen numero, -lla, Se on koordinaatti "x" (tai abskissa) ja toinen numero, b -, Se on koordinaatti "Y": ssä (tai tilattu). Merkintää käytetään P = (-lla,b --A.
On selvää, että Cartesian taso rakennettiin, että alkuperä vastaa “y” -akselin ”X” ja 0 -akselia, ts, JOMPIKUMPI= (0,0).
Cartesian lentokoneen cuadies
Kuten edellisissä kuvioissa voidaan nähdä, koordinaattiakselit tuottavat neljä eri aluetta, jotka ovat Cartesian -tason kvadrantteja, joita kirjaimet merkitään ja, II, III ja IV Ja nämä eroavat toisistaan merkissä, että kussakin niistä ovat.
Voi palvella sinua: algebrallinen päättelyKvadrantti Yllyttää
Kvadrantin kohdat Yllyttää He ovat niitä, joilla on molemmat koordinaatit, joilla on positiivinen merkki, toisin sanoen heidän X -koordinaatinsa ja koordinaatinsa ja positiiviset.
Esimerkiksi kohta P = (2,8). Se kuvaa sitä, piste 2 sijaitsee “X” -akselilla ja pisteellä 8 “y” -akselilla, sitten vedetään pystysuorat ja vaakasuorat viivat ja missä ne leikkaavat, missä piste on P.
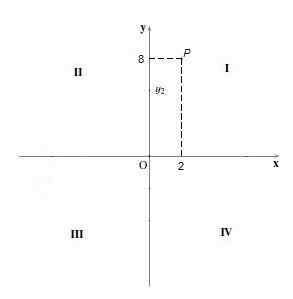
Kvadrantti II
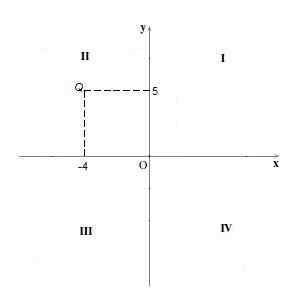
Kvadrantin kohdat II Heillä on negatiivinen "X" -koordinaatti ja positiivinen "Y" -koordinaatti. Esimerkiksi kohta Q = (-4,5). Se on graafista menettelyä kuten edellisessä tapauksessa.
Kvadrantti III
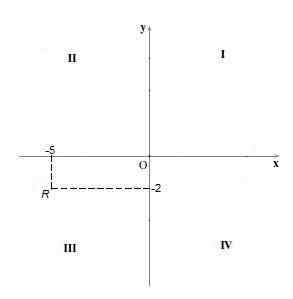
Tässä kvadrantissa molempien koordinaattien merkki on negatiivinen, toisin sanoen koordinaatti "x" ja koordinaatti "Y" ovat negatiivisia. Esimerkiksi kohta r = (-5, -2).
Kvadrantti IV
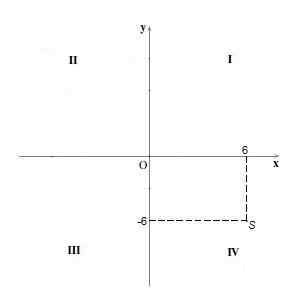
Kvadrantissa IV Pisteillä on positiivinen ja koordinaatti Y -negatiivinen koordinaatti. Esimerkiksi kohta S = (6, -6).

Viitteet
- Fleming, w., & Varberg, D. (1991). Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
- Larson, r. (2010). Esikuva (8 Ed.-A. Cengage -oppiminen.
- Uskollinen, j. M., & Viloria, N. G. (2005). Litteä analyyttinen geometria. Mérida - Venezuela: Venezuelan toimituksellinen C. -Lla.
- Oteyza, E. (2005). Analyyttinen geometria (Toinen Ed.-A. (G g. T. Mendoza, Ed.) Pearson Education.
- Oteyza, E. d -d., Osnaya, E. Lens., Garciadiego, c. H., Hoyo, a. M., & Flores,. R -. (2001). Analyyttinen geometria ja trigonometria (Ensimmäinen Ed.-A. Pearson -koulutus.
- Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen (Yhdeksäs ed.-A. Prentice Hall.
- Scott, c. -Lla. (2009). Cartesian lentokoneen geometria, osa: Analyyttiset kartiot (1907) (Uusintapainos ED.-A. Salamanlähde.

