Virtatiheys Sähkön johtavuus ja esimerkit

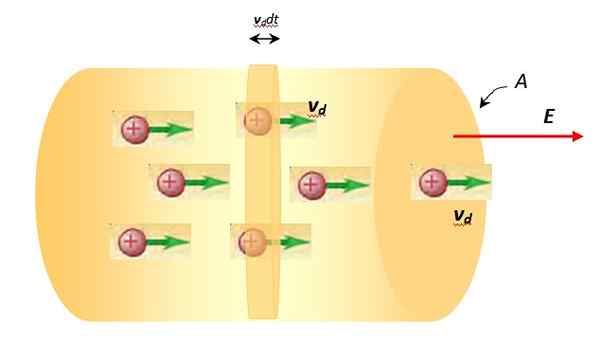
Sitä kutsutaan nykyinen tiheys Kuljettajan kautta virran määrään alueyksikköä kohti. Se on vektorin suuruus, ja sen moduuli antaa välittömän virran välillä ja ylittää kuljettajan poikkileikkauksen ja saman alueen, niin että:

Virtatiheysvektorin suunta on normaalin yksikkövektorin suunta poikkileikkaukseen n, ja lopulta suunta on sama kuin virra, jota valmistelukunnassa pidetään sellaisena, joka positiivisilla kuormittajilla olisi.

Tällä tavoin virrantiheysvektorin kansainvälisen järjestelmän yksiköt ovat AMP: t neliömetriä kohti: A/M². Virtatiheys on vektorisesti:

Seuraavassa kuvassa virrantiheysvektori, jonka suuruus on tässä tapauksessa J (Y, Z), toisin sanoen koordinaattitoiminto J -, ja, ja z -z. S on ristileikkausalue, joka on havainnollistettu neliö, mutta sillä voi olla mikä tahansa muu muoto, se on yleensä pyöreä.

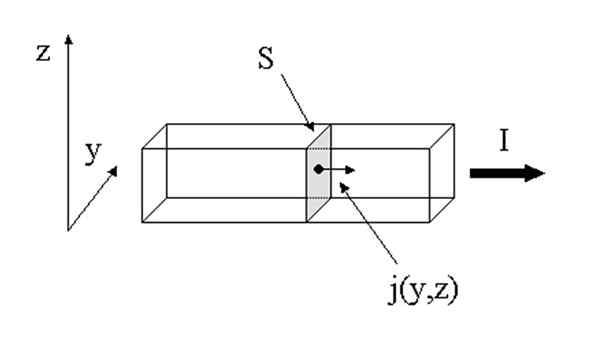Virtatiheysvektori. Lähde: Wikimedia Commons.

Virran virrantiheys ja voimakkuus liittyvät toisiinsa, vaikka ensimmäinen on vektori ja toinen ei ole. Virta ei ole vektor.

Kuljettajan sisälle perustettu sähkökenttä on kuitenkin vektori, ja se liittyy virtaan. Intuitiivisesti ymmärretään, että kenttä on voimakkaampi, kun virta on myös voimakkaampi, mutta kuljettajan poikkileikkauksella on myös ratkaiseva rooli tässä näkökulmassa.

[TOC]

Sähkökäyttömalli

Pala neutraalin johtavan johtimen, kuten kuviossa 3 esitetyn, lieriömäisellä tavalla kuormituskantajat liikkuvat satunnaisesti mihin tahansa suuntaan. Kuljettajan sisällä hänen tekemänsä aineen tyypin mukaan n kuormituskuljettajat yksikköä kohti. Tätä n ei pidä sekoittaa normaaliin vektoriin, joka on kohtisuorassa johtavaan pintaan nähden.

Pala lieriömäinen johdin näyttää nykyisten kantajien sisällä, jotka liikkuvat eri suuntiin. Lähde: Itse tehty.

Ehdotettu käyttäytymismallimalli koostuu kiinteästä ionisesta verkosta ja elektronikaasusta, jotka ovat nykyisiä operaattoreita, vaikka ne olisivat tässä edustettuna A +-merkillä, koska tämä on virran yleissopimus.

Mitä tapahtuu, kun kuljettaja yhdistyy akkuun?

Silloin kuljettajan päättyjen välinen potentiaalinen ero muodostuu lähteen ansiosta, joka vastaa työn tekemisestä: akku.

Voi palvella sinua: taivaalliset ruumiit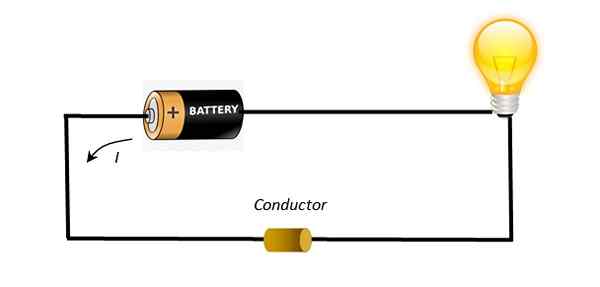Yksinkertainen piiri näyttää akun, joka kuljettajan johtimilla kytkeytyy polttimoon. Lähde: Itse tehty.

Tämän potentiaalieron ansiosta nykyiset kantajat kiihtyvät ja marssivat järjestyksessä kuin silloin, kun materiaali oli neutraalia. Tällä tavalla pystyt sytyttämään näytetyn piirin lampun.

Tässä tapauksessa kuljettajan sisälle on luotu sähkökenttä, joka kiihtyy elektroneihin. Tietysti näiden polku ei ole vapaa: vaikka elektronit ovat kiihtyviä, koska ne törmäävät kiteiseen verkkoon, he luopuvat osan energiastaan ​​ja hajoavat koko ajan. Globaali tulos on, että he liikkuvat hieman enemmän materiaalissa, mutta varmasti heidän edistymisensä on hyvin vähän.

Kun he törmäävät kiteiseen verkkoon, he saavat sen värähtelemään, mikä johtaa kuljettajan lämmitykseen. Tämä on vaikutus, joka on helposti havaittu: johtavat kaapelit lämmitetään, kun ne ylittävät sähkövirta.

Vedä nopeus v_{d -d}  ja virrantiheys

Nykyisillä kantajilla on nyt globaali liike samaan suuntaan kuin sähkökenttä. Sitä globaalia nopeutta, jota heillä on, kutsutaan vedonlyönti jompikumpi aalto nopeus Ja sitä symboloidaan v_{d -d}.

Kun potentiaaliero on muodostettu, nykyisillä kantajilla on järjestettävä liike. Lähde: Itse tehty.

Se voidaan laskea joillakin yksinkertaisilla näkökohdilla: kunkin hiukkasen kuljettajan sisällä kuljettu etäisyys aikavälillä DT On v_{d -d} . DT. Kuten aiemmin sanottiin, on n Hiukkaset tilavuusyksikköä kohti, tilavuus on poikkileikkauksen A pinta -alan tuote kulkevalla etäisyydellä:

V = a.v_{d -d} DT

Jos jokaisella hiukkasella on kuorma Q, kuinka paljon DQ: n kuormitusta kulkee alueen läpi -Lla Aikavälillä DT?-

dq = q.n. -Lla.v_{d -d} DT

 

Pikavirta on vain DQ/DT, siksi:

Ja jakautuminen A: n välillä saadaan virrantiheysvektori j:

J - = q.n.v_{d -d}

Kun kuorma on positiivinen, v_{d -d} on samaan suuntaan kuin JA  ja J -. Jos kuorma olisi negatiivinen, v_{d -d}  on vastapäätä kenttää JA, mutta J - ja JA Heillä on edelleen sama osoite. Toisaalta, vaikka virta olisi sama koko piirin ajan, virrantiheys ei välttämättä pysy ennallaan. Esimerkiksi, se on alhaisempi akun, jonka poikkileikkauspinta -ala on suurempi kuin ajojohdoissa, ohuempi.

Materiaalin johtavuus

Voidaan ajatella, että kuljettajan sisälle liikkuvat kuormittajat ja törmäävät jatkuvasti kiteiseen verkkoon, kohtaavat voiman, joka vastustaa niiden etenemistä, eräänlaista kitkaa tai hajoavaa voimaa F_{d -d} joka on verrannollinen heidän kantamaansa keskimääräiseen nopeuteen, ts. Vedonopeuteen:

Voi palvella sinua: kitkan edut ja haitat

F_{d -d} ∝ v

F_{d -d} = α. v_{d -d}

Tämä on Drude-Lorentz-malli, joka on luotu 1900-luvun alussa selittämään nykyisten kuljettajien liikkumisen kuljettajan sisällä. Ei ota huomioon kvanttivaikutuksia. α on suhteellisuusvakio, jonka arvo on materiaalin ominaisuuksien mukaan.

Jos vedonopeus on vakio, nykyiseen kantajalle vaikuttavien voimien summa on nolla. Toinen voima on sähkökenttä, jonka suuruus on Fe = Q.JA-

qe - α. v_{d -d} = 0

Vedonopeus voidaan ilmaista nykyisen tiheyden suhteen, jos se puhdistetaan kätevästi:

Siksi:

Mistä:

J = nq²E/α

Vakiot n, q ja a on ryhmitelty yhdeksi puheluksi σ, niin että se lopulta saadaan:

 J - = σJA

Ohmin laki

Virtatiheys on suoraan verrannollinen kuljettajan sisälle perustettuun sähkökenttään. Tähän tulokseen se tunnetaan nimellä Ohmin laki mikroskooppisessa muodossa tai paikallisessa Ohm -laissa.

Arvo σ = n.Q -² / α on vakio, joka riippuu materiaalista. Kyse on sähkönjohtavuus tai yksinkertaisesti johtavuus. Sen arvot on taulukko monille materiaaleille, ja niiden yksiköt kansainvälisessä järjestelmässä ovat AMPS/voltt x metri (A/V.m), vaikka on muitakin yksiköitä, esimerkiksi S/M (Siemens metriä kohti).

Kaikki materiaalit eivät noudata tätä lakia. Ne, jotka tekevät Ohmismateriaalit.

Aineessa, jolla on korkea johtavuus. Esimerkkejä materiaaleista, joilla on korkea johtavuus, ovat: grafeeni, hopea, kupari ja kulta.

Sovellusesimerkit

-Ratkaistu esimerkki 1

Löydä ilmaisten elektronien vetämisnopeus poikkileikkauksen 2 mm kuparikaapelista² Kun virta 3 kulkee sen läpi. Copperilla on 1 ajoelektroni atomia kohti.

Tosiasia: Avogadro -numero = 6 023 10²³ hiukkaset mol; Elektronikuorma -1.6 x 10^-19 C; Kuparitiheys 8960 kg/m³; Kuparimolekyylipaino: 63,55 g/mol.

Ratkaisu

- J - = q.n.v_{d -d} Vedonopeuden suuruus puhdistetaan:

Laskelmien helpottamiseksi, n, joka on kuormituskantajien lukumäärä yksikkötilavuutta kohti, niin J: n suuruus määritetään ja lopulta kaikki korvataan edellisessä lausekkeessa:

Voi palvella sinua: kategorinen muuttuja: Ominaisuudet ja esimerkit

Kuinka valot tulevat heti?

Tämä nopeus on yllättävän. Esimerkiksi se voi viedä elektronin melkein tunnin ajan autoakusta majakan polttimoon.

Onneksi sinun ei tarvitse odottaa niin kauan valojen sytyttämistä. Akun elektroni työntää nopeasti muita kuljettajan sisälle, ja siten sähkökenttä on perustettu hyvin nopeasti, koska se on sähkömagneettinen aalto. Häiriöt leviää johdon sisälle.

Elektronit onnistuvat hyppäämään atomin valon nopeudella viereiseen ja virta alkaa virtaa samalla tavalla kuin vesi tekee sen letkun läpi. Pisarat letkun alussa eivät ole samoja kuin poistumisessa, mutta se on myös vesi.

-Ratkaistu esimerkki 2

Kuva näyttää kaksi kytkettyä johtoa, jotka on valmistettu samasta materiaalista. Vasemmalta ohuempaan osaan tulevan virran on 2 -. Siellä 8: n elektronien veto nopeus.2 x 10^-4 neiti. Olettaen, että virran arvo pysyy vakiona, löytää elektronien vetämisnopeus oikean osassa, m/s.

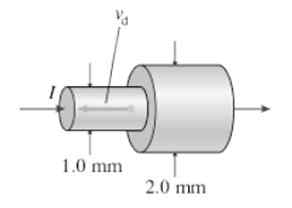
Ratkaisu

Ohuemmassa osassa: J₁ = n.Q -. v_D1 = I/a₁

Ja paksimmissa osassa: J₂ = n.Q -. v_D2 = I/a₂

Virta on sama molemmille osioille, samoin kuin n ja Q -, siksi:

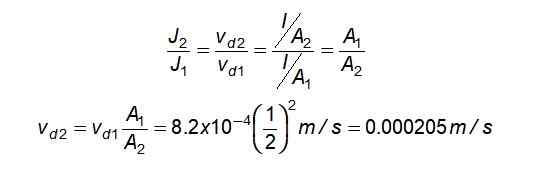Vedonopeus on alhaisempi laajemmassa osassa, jota odotettiin.

Viitteet

1. Resnick, r. 1992.Fyysinen. Kolmas painos laajennettu espanjaksi. Nide 2. Mannertoimitusyhtiö S.-Lla. C: n.V.
2. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Nide 2. 817-820.
3. Serway, R., Jewett, J. 2009. Tiede- ja tekniikkafysiikka modernin fysiikan kanssa. 7. painos. Nide 2. Cengage -oppiminen. 752-775.
4. Sevillan yliopisto. Sovelletun fysiikan laitos III. Tiheys ja virran voimakkuus. Toipunut: meistä.On
5. Walker, J. 2008. Fysiikka. 4. ed. Pearson.725-728.