Algebralliset johdannaiset

Mitkä ovat algebralliset johdannaiset?

Se algebralliset johdannaiset Ne koostuvat johdannaisen tutkimuksesta algebrallisten funktioiden tapauksessa. Johdannaisen käsitteen alkuperä juontaa juurensa muinaiseen Kreikkaan. Tämän käsitteen kehitystä motivoi tarve ratkaista kaksi tärkeää ongelmaa, toinen fysiikassa ja toinen matematiikassa.

Fysiikassa johdannainen ratkaisee liikkuvan esineen hetkellisen nopeuden määrittämisen ongelman. Matematiikassa se mahdollistaa tangenttiviivan löytämisen käyrälle tietyssä vaiheessa.

Vaikka on todella paljon enemmän ongelmia, jotka ratkaistaan ​​käyttämällä johdannaista, samoin kuin sen yleistyksiä, tulokset, jotka myöhemmin tulivat heidän konseptinsa käyttöönottoon.

Differentiaalilaskennan pioneerit ovat Newton ja Leibniz. Ennen muodollisen määritelmän antamista kehitämme taustan, matemaattisesta ja fyysisestä näkökulmasta.

Johdannainen odotettaessa tangenttiviivaa käyrään

Oletetaan. Haluamme löytää tangenttiviivayhtälön funktiolle F pisteestä A.

Otetaan toinen kohta p = (x, f (x)) kaaviosta, lähellä pistettä A, ja jäljitetään kuivauslinja, joka kulkee A- ja P: n läpi. Kuivausviiva on viiva, joka leikkaa käyrän kuvaajaan yhteen tai useampaan pisteeseen.

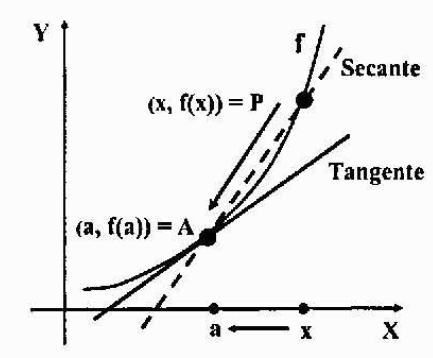
Saadaksesi haluamamme tangenttiviiva.

Jos siirrämme pisteen P graafin mukaan ja lähestymme sitä yhä enemmän pisteeseen A, aiemmin mainittu kuiva viiva lähestyy tangenttiviivaa, jonka haluat löytää. Rajan ottaminen, kun "P: llä on taipumus", molemmat linjat ovat samat, siksi myös niiden rinteet.

Secant -viivan kaltevuus on annettu

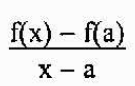
Sanoa, että p on lähellä A: ta, vastaa sanomista, että "x" lähestyy "a". Siten tangenttiviivan kaltevuus F: n kuvaajaan pisteessä A on yhtä suuri kuin:

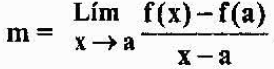
Aikaisempi lauseke on merkitty f '(a), ja se määritellään funktion f johdannaiseksi pisteessä "a". Näemme, että analyyttisesti funktion johdannainen pisteessä on raja, mutta geometrisesti se on linjan tangentti funktion kaaviolle pisteessä.

Voi palvella sinua: satunnaismuuttuja: käsite, tyypit, esimerkit

Nyt näemme tämän käsitteen fysiikan näkökulmasta. Saavutamme saman rajan saman lausekkeen, vaikkakin eri polulla, mikä saa määritelmän yksimielisyyden.

Johdannainen liikkuvan esineen hetkellinen nopeus

Katsotaanpa lyhyt esimerkki siitä, mitä hetkellinen nopeus tarkoittaa. Kun esimerkiksi sanotaan, että määränpäähän päästävä auto teki sen nopeudella 100 km tunnissa, se tarkoittaa, että tunnissa hän matkusti 100 km.

Tämä ei välttämättä tarkoita, että koko tunnin aikana auto oli aina 100 km, auton vekimetri pystyi jossain hetkessä merkitä vähemmän tai enemmän. Jos hänellä oli tarve seistä liikennevalolla, nopeus tuolloin oli 0 km. Tunnin kuluttua reitti oli kuitenkin 100 km.

Tätä kutsutaan keskimääräiseksi nopeudeksi, ja sen annetaan kuluneen ajanjakson välillä kuluneen etäisyyden osalta, kuten olemme juuri nähneet. Sillä välin nopeus on se, joka merkitsee auton velokimittarin neulaa tietyllä hetkellä (aika).

Katsotaanpa tämä nyt yleisempi tapa. Oletetaan, että objekti liikkuu viivaa pitkin ja että tätä siirtymää edustaa yhtälön s = f (t), jossa muuttuja t mittaa aikaa ja muuttujaa S siirtymää ottaen huomioon sen alun hetkessä t = 0, jolloin se on myös nolla, ts. F (0) = 0.

Tämä funktio F (t) tunnetaan sijaintifunktiona.

Kohteen hetkellisen nopeuden lauseke haetaan kiinteällä välittömällä. Tällä nopeudella merkitsemme sitä V (a).

Olipa se hetki lähellä välitöntä "a". Aikavälillä A: n ja "T": n välillä aseman muutoksen annetaan f (t) -f (a).

Keskimääräinen nopeus tällä aikavälillä on:

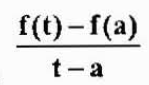
Joka on likiarvo hetkellisestä nopeudesta v (a). Tämä lähestymistapa on parempi, kun t lähemmäksi "a". Siksi,

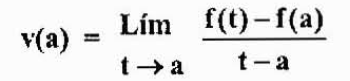
Huomaa, että tämä ilmaisu on yhtä suuri kuin edellisessä tapauksessa saatu, mutta eri näkökulmasta. Tätä kutsutaan f -funktion johdannaiseksi pisteessä "a", ja sitä merkitään f '(a), kuten yllä todettiin.

Voi palvella sinua: Eksponenttien lait

Huomaa, että muutoksen tekeminen h

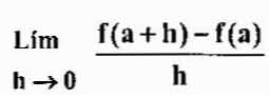
Molemmat lausekkeet ovat vastaavia, mutta joskus sitä tulisi käyttää enemmän toiseen, tapauksesta riippuen.

Sitten se määritetään yleisemmin, mikä johdetaan funktiosta f missä tahansa kohdassa "x", joka kuuluu sen verkkotunnukseen

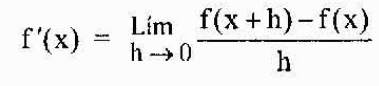
Tavallisin merkintä, joka edustaa funktion y = f (x) johdannaista on juuri näkemämme (f 'o y'). Toinen laajalti käytetty merkintä on kuitenkin Leibnizin merkintä, jota esitetään seuraavina lausekkeina:

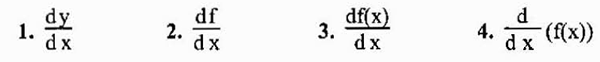
Ottaen huomioon, että johdannainen on pohjimmiltaan raja, sitä voi olla tai ei ole, koska rajoja ei aina ole. Jos sitä on, sanotaan.

Algebrallinen toiminta

Algebrallinen funktio on polynomien yhdistelmä summien, vähennysten, tuotteiden, osuuden, voimien ja radikaalien avulla.

Polynomi on muodon ilmaisu

P_n= a_nxⁿ+ -lla_N-1x^N-1+ -lla_N-2x^N-2+… + A₂x²+ -lla₁x+a_{0 -}

Missä n on luonnollinen luku ja kaikki_Yllyttää, I = 0,1,…, n ovat rationaalisia lukuja ja_n≠ 0. Tässä tapauksessa sanotaan, että tämän polynomin aste on n.

Seuraavat ovat esimerkkejä algebrallisista toiminnoista:

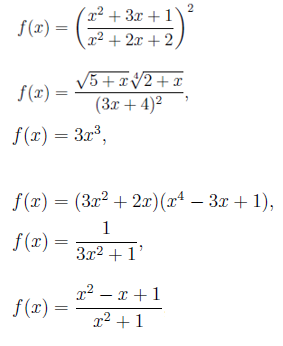
Tässä eksponentiaalisia, logaritmisia ja trigonometrisiä toimintoja ei sisälly hintaan. Johtajasäännöt, jotka näemme alla, ovat päteviä toimintoihin yleensä, mutta rajoitamme ja soveltamme niitä algebrallisten toimintojen tapauksessa.

Sääntöjä

Johdettu vakiosta

Toteaa, että vakion johdannainen on nolla. Eli jos f (x) = c, niin f '(x) = 0. Esimerkiksi vakiofunktion 2 johdannainen on yhtä suuri kuin 0.

Johdettu voimasta

Jos f (x) = xⁿ, sitten f '(x) = nx^N-1. Esimerkiksi X -johdannainen³ Se on 3x². Tämän seurauksena saadaan, että identiteetfunktion f (x) = x johdettu on f '(x) = 1x^1-1= x^{0 -}= 1.

Toinen esimerkki on seuraava: olkoon f (x) = 1/x², sitten f (x) = x^-2 ja f '(x) = -2x^-2-1= -2x^-3.

Tämä ominaisuus on myös päteviä juuria, koska juuret ovat rationaalisia voimia ja yllä olevaa voidaan soveltaa myös siinä tapauksessa. Esimerkiksi neliöjuurista johdettu

Se voi palvella sinua: arviointia välein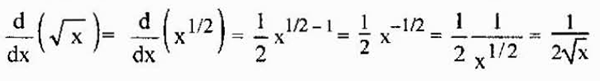

Johdettu summa ja vähennys

Jos F ja G ovat erotettavissa olevia funktioita x: ssä, niin myös summa f+g on ja on toteutettu, että (f+g) '(x) = f' (x)+g '(x) (x) (x).

Samoin sinun on (f -g) '(x) = f' (x) -g '(x). Toisin sanoen summan johdannainen (vähennys) on johdannaisten summa (tai vähennys).

Esimerkki

Jos h (x) = x²+X-1, sitten

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Tuotteesta johdettu tuote

Jos F ja G ovat erotettavissa olevia toimintoja X: ssä, niin FG -tuote on myös erotettavissa X: ssä ja on toteutettu

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Seurauksena on, että sillä on, jos C on vakio ja F on erilainen funktio x: ssä, niin CF on myös erotettavissa x y (vrt.) (X) = cf '(x).

Esimerkki

Jos f (x) = 3x (x²+1), sitten

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Osoitettua osamäärää

Jos F ja G ovat erotettavissa x ja g (x) ≠ 0, niin f/g on myös erotettavissa X: ssä, ja se on täytetty

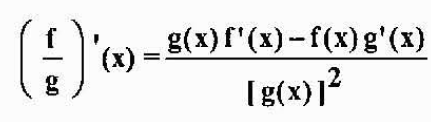
Esimerkki: Jos h (x) = x³/(x²-5x), sitten

H '(x) = [(x³) '(X⁵-5x)-(x³) (x⁵-5x) ']/ (x⁵-5x)²= [(3x²) (x⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Ketjusääntö

Tämä sääntö antaa mahdollisuuden saada toimintojen koostumuksen. Se muodostaa seuraavan: Jos y = f (u) on erotettavissa u: ssa ja u = g (x) on erotettavissa x: ssä, niin yhdistelmäfunktio F (g (x)) on erotettavissa X: ssä, ja se toteutetaan [F (F (F (F (F ( '= f' (g (x)) g '(x).

Toisin sanoen yhdistefunktion johdannainen on ulkoisen funktion (ulkoinen johdannainen) johdannaisen tuote johdetun sisäisen funktion (sisäinen johdannainen) tuote (sisäinen johdannainen).

Esimerkki

Jos f (x) = (x⁴-2x)³, niin

f '(x) = 3 (x⁴-2x)²(x⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

On myös tuloksia funktion käänteisen johdannaisen laskemiseksi, samoin kuin yleistäminen korkeamman asteen johdannaisiin. Sovellukset ovat laajoja. Heistä korostetaan heidän optimoinnin ja vähimmäisfunktioiden voitot.

Viitteet

1. Alarcon, S., González, M., & Quintana, H. (2008). Erilainen laskenta. ITM.
2. Cabrera, v. M. (1997). 4000 laskenta. Toimitusohjelma.
3. Castaño, H. F. (2005). Matematiikka ennen laskentaa. Medellinin yliopisto.
4. Eduardo, n. -Lla. (2003). Johdanto laskelmaan. Umbral Editions.
5. Lähteet, a. (2016). Perusmatiikka. Johdatus laskelmaan. Lulu.com.
6. Purcell, E. J -., Rigdon, S. JA., & Varberg, D. JA. (2007). Laskeminen. Pearson -koulutus.
7. Saenz, J. (2005). Erilainen laskenta (Toinen Ed.-A. Barquisimeto: Hypotenusa.
8. Thomas, G. B -., & Weir, M. D -d. (2006). Laskenta: useita muuttujia. Pearson -koulutus.