Demonstraatiokolmion, esimerkit, harjoitukset ratkaistu

Sitä kutsutaan Kolmion eriarvoisuus omaisuudelle, joka täyttää kaksi todellista lukua, joka koostuu sen summan absoluuttisesta arvosta, on aina pienempi tai yhtä suuri kuin sen absoluuttisten arvojen summa. Tämä ominaisuus tunnetaan myös nimellä Minkowski -eriarvoisuus tai kolmion muotoinen eriarvoisuus.

Tätä numeron ominaisuutta kutsutaan kolmionmuotoiseksi epätasa -arvoksi, koska kolmioissa tapahtuu, että toisen puolen pituus on aina pienempi tai yhtä suuri kuin kahden muun summa, vaikka tätä eriarvoisuutta ei aina sovelleta kolmioiden kentällä.

Kuvio 1. Kahden numeron summan absoluuttinen arvo on aina pienempi tai yhtä suuri kuin sen absoluuttisten arvojen summa. (Valmistettu r. Pérez)

Realissa on useita kolmionmuotoisia eriarvoisuuksia, mutta tässä tapauksessa valitsemme absoluuttisen arvon ja neliöbinomin ominaisuuksien perusteella.

Lause: Kaikille numeroparille -lla ja b - Todellisten numeroiden kuuluu, sen on:

Ja A + B | ≤ | A | + | B |

[TOC]

Esittely

Aloitamme harkitsemalla eriarvoisuuden ensimmäistä jäsentä, joka leikataan:

Ja A + B |^2 = (A + B)^2 = A^2 + 2 A B + B^2 (EC. 1)

Edellisessä vaiheessa ominaisuus on käytetty, että mikä tahansa neliön suuri luku on yhtä suuri kuin mainitun luvun absoluuttinen arvo, joka on korkea neliölle, toisin sanoen: | x |^2 = x^2. Neliöbinomin kehitystä on myös käytetty.

Kaikki numero x Se on pienempi tai yhtä suuri kuin sen absoluuttinen arvo. Jos lukumäärä on positiivinen, se on tasa -arvon arvoinen, mutta jos luku on negatiivinen, se on aina pienempi kuin positiivinen luku. Tässä tapauksessa sen oma absoluuttinen arvo, toisin sanoen x ≤ | X |.

Voi palvella sinua: epälineaarinen ohjelmointi: menetelmät ja harjoitukset

Tuote (a b) Se on numero, joten sovelletaan (a b) ≤ | A B |. Kun tätä ominaisuutta sovelletaan (EY. 1) Meillä on:

Ja A + B |^2 = A^2 + 2 (A B) + B^2 ≤ A^2 + 2 | A B | + B^2 (EY. 2)

Ottaen huomioon sen Ja A b | = | A || B | LA (EY. 2) Se voidaan kirjoittaa seuraavasti:

 Ja A + B |^2 ≤ A^2 + 2 | A || B | + B^2 (EY. 3)

Mutta kuten aiemmin sanomme, että numeron neliö on yhtä suuri kuin neliölle korkean numeron absoluuttinen arvo, yhtälö 3 voidaan kirjoittaa uudelleen seuraavasti:

 Ja A + B |^2 ≤ | A |^2 + 2 | A | | b | + | B |^2 (EY. 4)

Epätasa -arvon toisessa jäsenessä tunnustetaan huomattava tuote, joka sovellettaessa johtaa:

 Ja A + B |^2 ≤ (| A | + | B |)^2 (EC. 5)

Edellisessä ilmaisussa on huomattava, että molemmille epätasa -arvon jäsenille korottavat arvot ovat myös positiivisia, että on myös täytettävä, että:

 Ja A + B | ≤ (| A |+ | B |) (EY. 6)

Edellinen ilmaus on juuri se, mitä halusit osoittaa.

Esimerkit

Seuraavaksi tarkistamme kolmionmuotoisen eriarvoisuuden useiden esimerkkien kanssa.

Esimerkki 1

Arvo otetaan A = 2 ja arvo B = 5, toisin sanoen molemmat positiiviset luvut ja tarkistamme, täyttyykö epätasa -arvo vai ei.

 Ja 2 + 5 | ≤ | 2 |+ | 5 |

 Ja 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Tasa -arvo varmistetaan, joten kolmion epätasa -arvolause on toteutettu.

Esimerkki 2

Seuraavat arvot valitaan a = 2 ja b = -5, toisin sanoen positiivinen luku ja toinen negatiivinen, tarkistamme, täyttyykö epätasa -arvo vai ei.

Voi palvella sinua: Trinomial

 Ja 2 - 5 | ≤ | 2 |+ | -5 |

 Ja -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Epätasa -arvo toteutuu, joten kolmion muotoinen eriarvoisuuslause on varmistettu.

Esimerkki 3

Arvo otetaan A = -2 ja arvo B = 5, toisin sanoen negatiivinen luku ja toinen positiivinen, tarkistamme, täyttyykö epätasa -arvo vai ei.

 Ja -2 + 5 | ≤ | -2 |+ | 5 |

 Ja 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Epätasa -arvo vahvistetaan, joten lause on täytetty.

Esimerkki 4

Seuraavat arvot a = -2 ja b = -5 valitaan, ts. Molemmat negatiiviset luvut ja tarkistamme, täyttyykö epätasa -arvo vai ei.

 Ja -2 - 5 | ≤ | -2 |+ | -5 |

 Ja -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Tasa -arvo varmistetaan, joten Minkowskin eriarvoisuuslause on täytetty.

Esimerkki 5

Arvo otetaan A = 0 ja arvo B = 5, toisin sanoen nollumero ja toinen positiivinen, sitten tarkistamme, täyttyykö epätasa -arvo vai ei.

 Ja 0 + 5 | ≤ | 0 |+ | 5 |

 Ja 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Tasa -arvo toteutetaan, joten kolmion epätasa -arvolause on varmistettu.

Esimerkki 6

Arvo otetaan A = 0 ja arvo B = -7, toisin sanoen nollumero ja toinen positiivinen, sitten tarkistamme, täyttyykö epätasa -arvo vai ei.

 Ja 0 - 7 | ≤ | 0 |+ | -7 |

 Ja -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Tasa -arvo varmistetaan, joten kolmion muotoinen eriarvoisuuslause on täytetty.

Ratkaisut

Seuraavissa harjoituksissa edustaa geometrisesti kolmion epätasa -arvoa tai Minkowskin eriarvoisuutta numeroille A ja B.

Voi palvella sinua: papruda

Numero A esitetään segmentinä X -akselilla, sen alkuperästä tai samaan aikaan kuin X -akselin nolla ja segmentin toinen pää (pisteessä P) on positiivisessa suunnassa (oikealla) x -akseli, jos a> 0, mutta < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Samoin numero B esitetään segmentinä, jonka alkuperä on kohta P. Toinen pää, ts. Piste, joka on P: n oikealla puolella, jos B on positiivinen (b> 0) ja kohta q on | b | yksiköt P: n vasemmalla puolella, jos B<0.

Harjoitus 1

Edustavat graafisesti kolmion epätasa -arvoa a = 5 ja b = 3 Ja A + B | ≤ | A | + | B |, olemus C = a + b. 

Ratkaisu 1: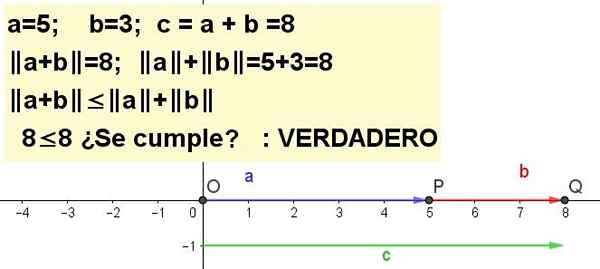

Harjoitus 2

Tee kolmion muotoinen epätasa -arvo kaavio a = 5 ja b = -3. 

Ja A + B | ≤ | A | + | B |, olemus C = a + b.

Ratkaisu 2:

Harjoitus 3

Kuvaa kolmion epätasa -arvoa a = -5 ja b = 3.

Ja A + B | ≤ | A | + | B |, olemus C = a + b. 

Ratkaisu 3: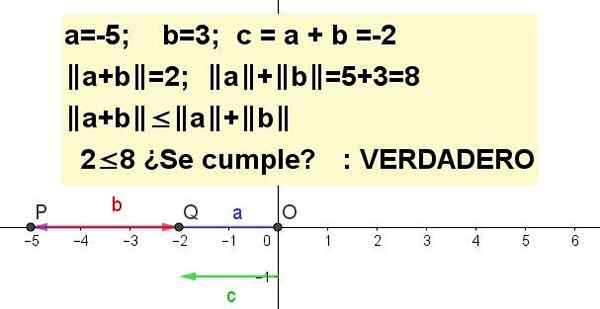

Harjoitus 4

Kuvaa kolmionmuotoinen eriarvoisuus a = -5: lle ja b = -3: lle.

Ja A + B | ≤ | A | + | B |, olemus C = a + b.

Ratkaisu 4: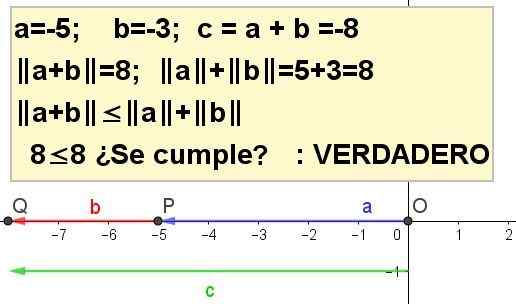

Viitteet

1. JA. Valkoinen. (1980).Boolen algebra ja sen sovellukset . Mannertoimitusyhtiö C. -Lla.
2. Mícheal tai 'searcoid.(2003) Abstraktin analyysin elementit ... matematiikan laitos. University College Dublin, Beldfield, Dublind.
3. J -. Van Wyk. (2006) Matematiikka ja tekniikka tietotekniikassa. Tietotekniikan ja tekniikan instituutti. Kansallinen standardilaitos. Washington, D. C. 20234
4. Eric Lehman. Tietotekniikan matematiikka.  Google Inc.
5. F Thomson Leighton (1980). Laskenta. Matematiikan laitos ja tietotekniikka ja AI -laboratorio, Massachussetts Institute of Technology.
6. Khan -akatemia. Kolmion eriarvoisuuslause. Toipunut: khanacademy.org
7. Wikipedia. Kolmion muotoinen eriarvoisuus. Palautettu: on. Wikipedia.com