Ero ympyrän ja kehän välillä (esimerkkien kanssa)

Se Ero ympyrän ja kehän välillä Se on seuraava: Ympyrä on ympyrän litteä, muotoiltu tai rajattu pinta, kun taas jälkimmäinen on litteä käyrä.

Usein molemmat käsitteet ovat hämmentyneitä, koska ne liittyvät toisiinsa, mutta sinun on aina muistettava, että ympärysmitta on ympyrän reuna, kun taas se sisältää kehän ja kaikki sen sisätilat.

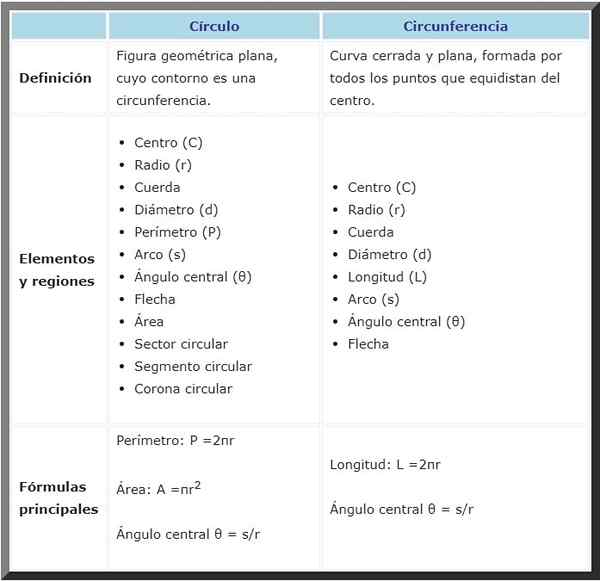
Molemmilla on muun muassa monia yhteisiä elementtejä, kuten keskusta, säde ja halkaisija, seuraavan vertailevan taulukon mukaan:

	Ympyrä	Ympärysmitta
Määritelmä	Litteä geometrinen hahmo, jonka muoto on kehä.	Suljettu ja litteä käyrä, muodostavat kaikki keskellä olevat kohdat, jotka ovat tasa -arvoisia.
Elementit ja alueet	Keskusta (c) Radio (R) Köysi Halkaisija (d) Kehä (p) Kaari (t) Keskuskulma (Θ-A Nuoli Alue Pyöreä sektori Pyöreä segmentti Pyöreä kruunu	Keskusta (c) Radio (R) Köysi Halkaisija (d) Pituus (l) Kaari (t) Keskipituus (Θ-A Nuoli
Kaavat	Kehä: p = 2π⋅r - Alue: A =πR2 Keski kulma: Θ= s/r	Pituus: L = 2π⋅r - Keski kulma: Θ= s/r

[TOC]

Ympyrä: Määritelmä, ominaisuudet ja osat

Ympyrä on tasainen geometrinen hahmo, joka sisältää kaikki muodon muodostavat kehän kohdat ja myös kaikki sisäpisteet.

Tästä syystä sille on ominaista:

-Reuna tai kehä, joka on ympyrän ympärysmitta.

-Pinnallinen alue.

Ympyrän elementit

Jokaisessa ympyrässä on seuraavat osat tai elementit:

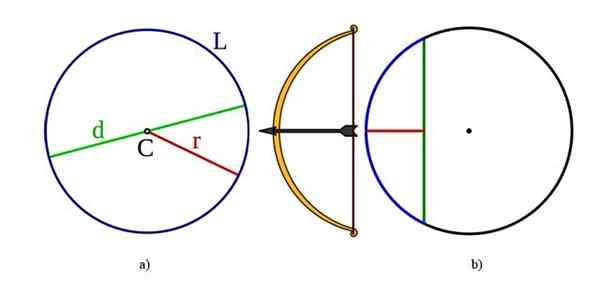Ympyrän elementit, jotka ovat myös yhteisiä kehälle: vasemmalle a) ovat keskusta D, halkaisija D, säde r ja pituus L L L L. Oikealla b) on köysi ja sagita tai nuoli. Lähde: Wikimedia Commons.

Keskusta: Mikä on kohta C, joka on yhtäläistä kaikki reunan kohteet.

Voi palvella sinua: ARC (geometria): Mitta, kaarien tyypit, esimerkit

Köysi: segmentti, joka yhdistää ympyrän reunan kaksi pistettä. Kuvassa b) oikealla, se on tummempi vihreä segmentti.

Halkaisija: kevyempi vihreä segmentti, merkitty "D" kuvassa A), joka yhdistää reunan kaksi pistettä ja kulkee samalla keskuksen läpi. Halkaisija on myös köysi, pisin kaikista, joten se tunnetaan nimellä Pääke.

Radio: Kuvassa A ”R” on merkitty punainen segmentti, joka liittyy ympyrän keskipisteeseen reunan pisteellä. Sen mitta on puolet halkaisijasta.

Keula: osa muotoa, joka on tämän kahden pisteen välillä, sinisellä kuvassa B).

Keskikulma: Se on kulma, jonka kärkipiste on keskellä tai ja sivut ovat ympyrän radioita.

Nuoli: segmentti kohtisuorassa köysiin (punaisella kuvassa B), joka liittyy köyden keskustaan ​​reunan pisteellä.

Pituus tai kehä: Se on ympyrän muodon mitta, merkitty l. Se riippuu radiosta r ja on verrannollinen irrationaaliseen lukumäärään π:

π = 3.1416 ..

Jotta:

L = 2π⋅r

Pyöreät alueet

Koska ympyrä on tasainen luku, on kokonaispinta -ala ja myös eri alueet. Tunnetuimmat ovat seuraavat:

Ympyräalue: Se on verrannollinen säteen neliöön, suhteellisuusvakio on luku π.

Soittamalla ympyrän alueelle, se ilmaistaan ​​seuraavasti:

A = πr²

Pyöreä segmentti: Se on osa ympyrästä, jota rajoittaa sininen kaari ja tummanvihreä köysi kuvassa B.

Voi palvella sinua: Lisäkulmat: Mitä ovat, laskenta, esimerkit, harjoitukset

Pyöreä sektori: Se on myös ympyrän alue, mutta se sisältyy kahden radion ja vastaavan kaarin välillä.

Pyöreä kruunu: Se on rengas muotoiltu ja sitä rajoittaa kaksi samankeskistä kehää, radio Menorin ulkopuolella ja radiokaupungin sisällä.

Ympäristö: DEfinitio, ominaisuudet ja osat 

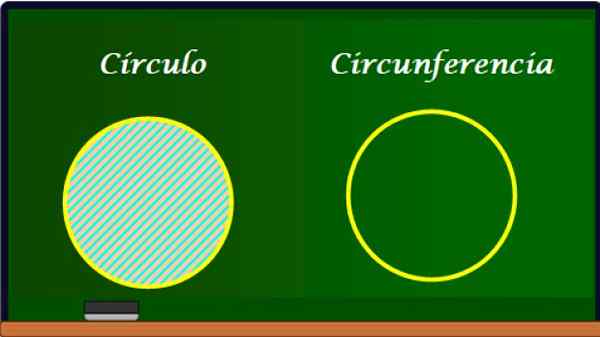Ympyrä ja sen ympärysmitta. Lähde: f. Zapata.

Ympäristö on ympyrän reuna, ja siksi sillä on monia yhteisiä elementtejä tämän kanssa. Ympäristöllä ei kuitenkaan ole aluetta, koska koska se on käyrä, sillä on vain pituus L.

Ympäristö määritellään muodollisesti kaikkien pisteiden joukkoksi, jotka rinnastavat toisesta keskuksesta tunnetusta pisteestä.

Sisustuspisteitä ei sisälly, koska ne vastaavat ympyrää.

Kehän elementit

Monet kehän elementit ovat samat kuin ympyrän, lukuun ottamatta niitä, jotka viittaavat alueille ja alueille, joten ylempi hahmo toimii referenssinä.

Meillä on sitten:

Keskusta: C: n merkitty ja joskus myös O, kaikki ympäryskohdat pitävät saman etäisyyden sen kanssa.

Köysi: segmentti, joka liittyy kahteen kehälle kuuluvaan pisteeseen.

Halkaisija: Se liittyy myös kahteen kehän pisteeseen, mutta kulkee aina saman keskuksen läpi.

Radio: Se on keskustan ja minkä tahansa kehän välinen etäisyys.

Keula: Se on osa kehästä.

Keskikulma: Se on kulma, jossa kärkipiste on keskusta C ja kaksi yhtä suurta sivua, mittaavat aivan kuten radio.

Nuoli: segmentti kohtisuorassa köysiin nähden, joka liittyy tämän keskustaan ​​vastaavalla kehän pisteellä.

Voi palvella sinua: Moninkertainen periaate: Laskentatekniikat ja esimerkit

Pituus tai kehä: Se on ympärysmitta, joka kuten olemme nähneet, on verrannollinen lukumäärään π = 3.1416… ja se lasketaan kaavalla:

L = 2π⋅r

Ympäristöyhtälö

A Piste P kuuluu kehälle niin kauan kuin sen etäisyys toiseen pisteeseen C on yhtä suuri kuin r -, radio.

Kaikilla Cartesian lentokoneella on koordinaatit (X, y) ja etäisyyden neliö d -d Kahden välillä, p₁(x₁,ja₁) Ja p₂(x₂,ja₂), annetaan kaavalla:

d -d₂² = (x₂ - x₁-A² +  (ja₂ - ja₁-A²

Otetaanko koordinaattien (x, y) pisteeseen ja koordinointiin pisteeseen C (H, K). Korvataan, edellinen yhtälö olisi tällainen:

(X - h)² +  (Y- k)² = r²

Tämä on ympärysyhtälö, että kaikki sen kohta täyttää. Jos kehän keskipiste on samaan aikaan koordinaattijärjestelmän alkuperän kanssa, niin h = k = 0 ja yhtälö yksinkertaistetaan:

x² + ja² = r²

Tarkastellaan esimerkkiä yhtälön käytöstä ja vastausta tähän asiaan: Kohta (4.6) kuuluu kehään (x - 1)² +  (ja - 2)² = 25?

Yhtälön pisteen koordinaattien selvittämiseksi korvataan, ja jos se on tasa -arvo, kohta kuuluu kehälle:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

Ja todellakin, kuten 25 = 25, päätellään, että (4.6) kuuluu kehään.

Viitteet

1. Ilmaiset matematiikan opetusohjelmat. Ympyrän alue ja kehä - geometrian laskin. Palautettu: Analysemath.com.
2. Matematiikan avoin viite. Ympyrä, ympyrän kehä. Toipunut: MathPenref.com.
3. Tiede. Kuinka löytää ympyrän kehä. Toipunut: tiedekunnasta.com.
4. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.