Erot nopeuden ja nopeuden välillä (esimerkkien kanssa)

Se Erot nopeuden ja nopeuden välillä On olemassa, vaikka molemmat ovat sukulaisia ​​fyysisiä määriä. Yleisellä kielellä yksi termi tai toinen käytetään keskenään ikään kuin ne olisivat synonyymejä, mutta fysiikassa on välttämätöntä erottaa ne.

Tässä artikkelissa molemmat käsitteet on määritelty, erot ilmoitetaan ja selitetään esimerkkien perusteella, miten ja milloin toinen tai toinen sovelletaan. Yksinkertaistamiseksi tarkastelemme liikkuvaa hiukkasia ja sieltä tarkistamme nopeuden ja nopeuden käsitteet. 

	Nopeus	Nopeus
Määritelmä	Se on ajomatkan päässä ajasta.	On siirtymä (tai aseman muutos) jokaisessa aikayksikössä.
Merkintä	v	v
Matemaattisen objektin tyyppi	Kiivetä.	Vektori.
Kaava (äärellisen ajanjakson ajan)*	v = ΔS/ s/Δt	v = ΔR/Δt
Kaava (tietyn ajan ajan) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Selitys kaavasta	*Kulkevan polun pituus jaettuna sen kuluttamiseen käytetyn ajanjakson välillä.** Hetkellä nopeudella aikavälillä on taipumus nolla. ** Matemaattinen toimenpide on radan johdannainen ajanjakson funktiona ajanjakson t.	*Vektorin siirtymä jaettuna ajanjaksolla, jolloin siirtymä tapahtui. ** Hetkellä ajanjakso on hetkessä nolla. ** Matemaattinen toimenpide on aseman johdannainen ajoissa.
Ominaisuudet	Sen ilmaisemiseksi vaaditaan vain positiivinen reaaliluku, riippumatta alueellisista mittoista, joissa liike tapahtuu. ** Välitön nopeus on hetkellisen nopeuden absoluuttinen arvo.	Sen ilmaisemiseksi voidaan tarvita enemmän kuin yksi reaaliluku (positiivinen tai negatiivinen) riippuen alueellisista mitoista, joissa liike tapahtuu. ** hetkellinen nopeusmoduuli on hetkessä.

Esimerkkejä yhtenäisellä nopeudella suorissa osissa

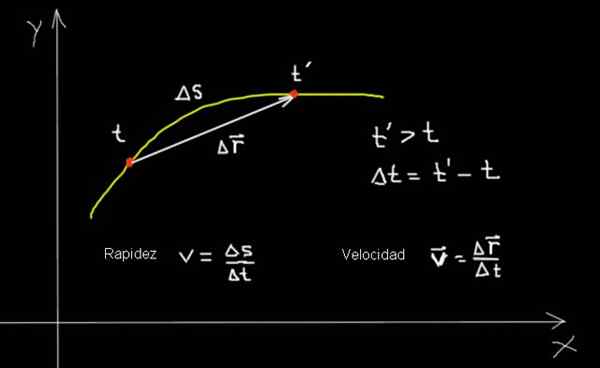
Käyrässä liikkuvan hiukkasen nopeus ja nopeus. Valmistaja: f. Zapata.

Edellisessä taulukossa tiivistettiin useita nopeuden ja nopeuden näkökohtia. Ja sitten täydentääkseen useita esimerkkejä, jotka kuvaavat mukana olevia käsitteitä ja niiden suhteita:

Voi palvella sinua: paramagnetismi

- Esimerkki 1

Oletetaan, että punainen muurahainen liikkuu suoran viivan jälkeen ja seuraavassa kuvassa ilmoitettuun suuntaan.

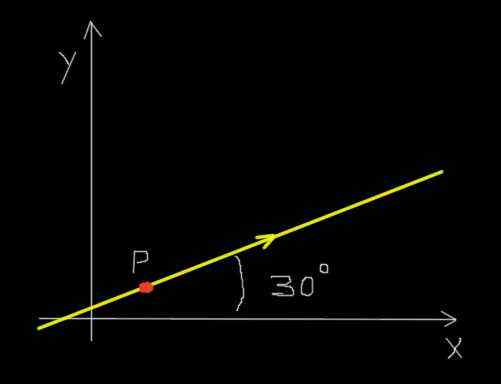Muurahainen suoraviivaisella polulla. Lähde: f. Zapata.

Lisäksi muurahainen liikkuu tasaisesti siten, että se kulkee 30 millimetrin etäisyydellä 0,25 sekunnissa. 

Määritä muurahaisen nopeus ja nopeus.

Ratkaisu 

Muurahaisen nopeus lasketaan jakamalla etäisyys ΔS Toure -kiertue Δt.

V = ΔS/Δt = (30 mm)/(0,25s) = 120 mm/s = 12 cm/s

ANT: n nopeus lasketaan jakamalla siirtymä Δr - sen ajanjakson ajan, jolloin mainittu siirtyminen tehtiin.

Siirtymä oli 30 mm suuntaan 30º X -akselin suhteen tai kompaktissa muodossa: 

Δr - = (30 mm ¦ 30º)

Voidaan huomata, että siirtymä koostuu suuruudesta ja osoitteesta, koska se on vektorimääritys. Vaihtoehtoisesti siirtymä voidaan ilmaista sen Cartesian -komponenttien X ja Y: n mukaan tällä tavalla:

Δr - = (30 mm* cos (30º); 30 mm* ilman (30º)) = (25,98 mm; 15,00 mm)

ANT: n nopeus lasketaan jakamalla siirtymä sen ajanjakson ajan, jolloin se suoritettiin:

v = Δr -/Δt = (25,98 mm / 0,25 s; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Tämä nopeus Cartesian komponenteissa X ja Y Y CM/S -yksiköissä on:

v = (10 392; 6 000) cm/s.

Vaihtoehtoisesti nopeusvektori voidaan ilmaista polaarisessa muodossaan (moduuli ¦ -suunta) kuvan osoittamalla tavalla:

v = (12 cm/s ¦ 30º).

Huomautus: Tässä esimerkissä, kun nopeus on vakio, keskimääräinen nopeus ja hetkellinen nopeus vastaavat. On todistettu, että hetkellinen nopeusmoduuli on heti nopea.

Voi palvella sinua: tiheys

Esimerkki 2

Edellisen esimerkin sama muurahainen siirtyy A: sta B: hen B: n jälkeen C: n jälkeen ja lopulta C: stä A: hon seuraavan kuvan esitetyn kolmion polun jälkeen.

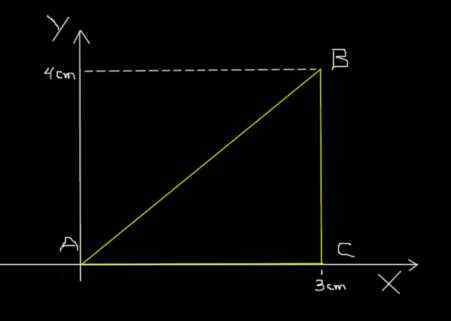Muurahaisen kolmion muotoinen polku. Lähde: f. Zapata.

Osa AB matkustaa 0,2S: llä; BC kulkee 0,1 sekunnissa ja lopulta CA matkustaa 0,3 sekunnissa. Laske ABCA -reitin keskimääräinen nopeus ja ABCA -reitin keskimääräinen nopeus.

Ratkaisu 

ANT: n keskimääräisen nopeuden laskemiseksi aloitamme määrittämällä kuluneen kokonaismatkan:

ΔS = 5 cm + 4 cm + 3 cm = 12 cm.

Koko matkalle käytetty aika on:

Δt = 0,2S + 0,1s + 0,3 s = 0,6 s.

Joten muurahaisen keskimääräinen nopeus on:

V = ΔS/ΔT = (12 cm)/(0,6s) = 20 cm/s.

Sitten ABCA -reitillä oleva muurahaisnopeus lasketaan. Tässä tapauksessa muurahaisen tekemä siirtymä on:

ΔR = (0 cm; 0 cm)

Tämä johtuu siitä, että siirtymä on ero lopullisen sijainnin välillä vähemmän alkuperäisessä sijainnissa. Koska molemmat asemat ovat samat, niin niiden ero on tyhjyys, mikä johtaa tyhjän siirtymän.

Tämä nolla -siirtymä suoritettiin 0,6 sekunnin ajanjaksolla, joten muurahaisen keskimääräinen tyyppi oli:

v =(0 cm; 0 cm)/ 0,6s = (0; 0) cm/ s.

Johtopäätös: Keskinopeus 20 cm/s, Mutta keskimääräinen nopeus on nolla ABCA -reitillä.

Esimerkkejä yhtenäisellä nopeudella kaarevia osia

Esimerkki 3

Hyönteinen liikkuu ympyrällä, joka on 0,2 m säde tasaisella nopeudella, niin että A: sta ja saavuttamisesta B, se kulkee ¼ kehästä 0,25 s.

Voi palvella sinua: Hydraulinen puristus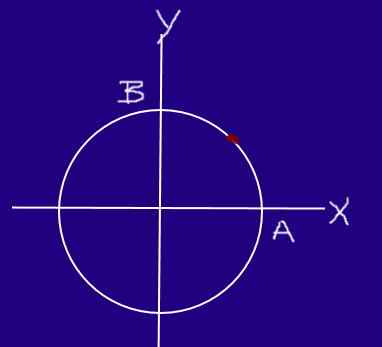Pyöreä osa hyönteinen. Lähde: f. Zapata.

Määritä hyönteisen nopeus ja nopeus osassa AB.

Ratkaisu 

Ympäristökaaren pituus A: n ja B: n välillä on:

ΔS = 2πr /4 = 2π (0,2m) /4 = 0,32 m.

Keskimääräisen nopeuden määritelmän soveltaminen:

V = ΔS/ΔT = 0,32 m/0,25 s = 1,28 m/s.

Keskimääräisen nopeuden laskemiseksi on tarpeen laskea siirtymävektori alkuperäisen aseman A ja lopullisen B: n välillä:

Δr - = (0; r)-(r; 0) = (-r; r) = (-0,2; 0,2) m

Keskimääräisen nopeuden määritelmän soveltaminen saadaan:

v = Δr -/ Δt = (-0,2; 0,2) m / 0,25s = (-0.8; 0,8) m/s.

Aikaisempi lauseke on keskimääräinen nopeus A: n ja B: n välillä, jotka ilmaistaan ​​Cartesian muodossa. Vaihtoehtoisesti keskimääräinen nopeus voidaan ilmaista polaarisessa muodossa, toisin sanoen moduulissa ja suunnassa:

Ja v Ja = ((-0,8)^2 + 0,8^2)^(½) = 1,13 m/s

Osoite = arctan (0,8 / (-0,8)) = Arcan (-1) = -45º + 180º = 135º X-akselin suhteen.

Lopuksi, keskimääräinen nopeusvektori polaarisessa muodossa on: v =(1,13 m/s ¦ 135º).

Esimerkki 4

Olettaen, että edellisen esimerkin hyönteisen lähtömomentti on 0: n pisteestä A, vektorisi sijainti on hetkessä, mikä on annettu:

r -(t) = [r cos ((π/2) t); R Sen ((π/2) t)].

Määritä nopeus ja välitön nopeus milloin tahansa T.

Ratkaisu 

Hetkellinen nopeus on johdannainen aseman ajan suhteen:

v(t) = Dr -/dt = [-r (π/2) ilman ((π/2) t); R (π/2) cos ((π/2) t)]]]

Välitön nopeus on vektorin välittömän nopeuden moduuli:

v (t) = Ja v(T) Ja = π r / 2^½

Viitteet

1. Alonso m., Suomalainen. Fysiikan osa I: Mekaniikka. 1970. Inter -American Educational Fund S.-Lla.
2. Hewitt, s. Käsitteellinen fysiikka. Viides painos. Pearson.
3. Nuori, Hugh. Yliopiston fysiikka, jolla on moderni fysiikka. 14. ed. Pearson.
4. Wikipedia. Nopeus. Palautettu: on.Wikipedia.com
5. Zita, a. Ero nopeuden ja nopeuden välillä. Haettu: erottaja.com