Dynamiikan historia, mitä tutkimuksia, lakeja ja teorioita

Se dynaaminen Juuri mekaniikan alue tutkii kehon ja niiden vaikutusten välistä vuorovaikutusta. Se käsittelee niiden kuvaamista laadullisesti ja kvantitatiivisesti sen lisäksi, kuinka ne kehittyvät ajan myötä.

Periaatteidensa soveltamisessa tiedetään, kuinka kehon liikettä muutetaan vuorovaikutuksessa muiden kanssa, ja myös jos nämä vuorovaikutukset vääristävät sitä, koska on täysin mahdollista, että molemmat vaikutukset tapahtuvat samanaikaisesti.

Kuvio 1. Pyöräilijöiden vuorovaikutukset muokkaavat heidän liikettään. Lähde: Pixabay.

Suuren kreikkalaisen filosofin Aristoteleen uskomukset (384-322.C.) voitti dynamiikan perustana lännessä vuosisatojen ajan. Hän ajatteli, että esineet liikkuivat jonkin tyyppisen energian takia, joka työnsi ne yhteen tai toiseen suuntaan.

Hän havaitsi myös, että vaikka esine työnnetään, se liikkuu vakiona nopeudella, mutta kun se lopettaa työntö.

Aristoteleen mukaan jatkuvan voiman toiminta oli välttämätöntä varmistaakseen, että jotain siirtyi jatkuvaan nopeuteen, mutta tapahtuu, että tällä filosofilla ei ollut kitkan vaikutuksia.

Toinen idea oli, että raskaimmat esineet putosivat nopeammin kuin kevyin. Se oli suuri Galileo Galilei (1564-1642), joka osoitti kokeilla, että kaikki ruumiit putoavat samalla kiihtyvyydellä heidän massastaan ​​riippumatta, halveksittaen viskooseja vaikutuksia.

Mutta toistaiseksi asunut Isaac Newton (1642-1727), merkittävin tutkija, jota pidetään modernin dynamiikan ja matemaattisen laskelman isänä yhdessä Gottfried Leibnizin kanssa.

Kuva 2. Godfrey Kneller Isaac Newton vuonna 1682. Lähde: Wikimedia Commons.

Sen kuuluisat lait, jotka on muotoiltu 1700 -luvulla. Ne muodostavat klassisen mekaniikan perustan, joka näemme ja vaikuttaa meihin päivittäin. Näistä laeista keskustellaan pian.

[TOC]

Mitä tutkitaan dynamiikkaa?

Dynamiikkatutkimuksen vuorovaikutus esineiden välillä. Kun esineet ovat vuorovaikutuksessa, niiden liikkeessä ja myös muodonmuutoksissa tapahtuu muutoksia. Erityinen staattinen alue on omistettu niille järjestelmille tasapainossa, jotka ovat levossa tai yhtenäisellä välittömällä siirtona.

Dynamiikan periaatteiden soveltaminen on mahdollista ennustaa yhtälöiden kautta, mitkä ovat muutokset ja objektien kehitys ajoissa. Tätä varten jotkut oletukset vahvistetaan sen tyypin mukaan, jonka haluat opiskella.

Hiukkaset, jäykät kiintoaineet ja jatkuvat keinot

Hiukkasmalli on yksinkertaisin aloittaa dynamiikan periaatteiden soveltaminen. Oletetaan, että tutkittavassa objektissa on massa, mutta ei mittoja. Siksi hiukkas voi olla yhtä pieni kuin elektroni tai yhtä suuri kuin maa tai aurinko.

Kun haluat tarkkailla dynamiikan koon vaikutusta, on tarpeen harkita esineiden kokoa ja muotoa. Malli, joka ottaa tämän huomioon, on jäykän kiinteän aineen, kehon, jonka mitattavissa olevat mitat koostuvat monista hiukkasista, mutta jota ei ole muodostettu voimien vaikutuksissa.

Lopuksi, jatkuva mediamekaniikka ottaa huomioon esineen ulottuvuudet, vaan myös niiden erityiset ominaisuudet, mukaan lukien kyky muodonmuutos. Jatkuvat väliaineet kattavat jäykät kiinteät aineet ja ne, jotka eivät ole nesteiden lisäksi.

Newtonin lait

Avain dynamiikan toiminnan ymmärtämiseen on Newtonin lakien ymmärtämisessä, jotka yhdistävät kvantitatiivisesti voimat, jotka toimivat ruumiissa muutoksissa heidän liikkumistilassaan tai lepotilassaan.

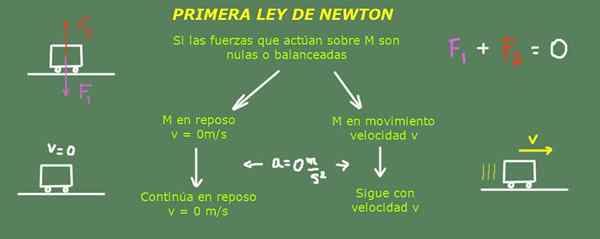
Newtonin ensimmäinen laki

Selitys Newtonin ensimmäisestä laista. Lähde: Itse tehty.

Sanoo niin:

Kun esineen nettovoima on yhtä suuri kuin nolla, esine jatkuu levossa, jos se oli levossa. Ja jos hän liikkui, hänen liikkeensa on suoraviivaista ja jatkuvasti.

Lausunnon ensimmäinen osa näyttää melko ilmeiseltä, koska on selvää, että levossa oleva esine pysyy näin, ellei se ole häiriintynyt. Ja tätä varten vaaditaan voima.

Voi palvella sinua: Democritus Atomic -malli: Tausta, ominaisuudet, postulaatit

Toisaalta se tosiasia, että esine pysyy liikkeessä, vaikka sen verkkovoima on nolla, on hiukan vaikeampi hyväksyä, koska näyttää siltä, ​​että esine voisi olla liikkeellä toistaiseksi. Ja jokapäiväinen kokemus kertoo meille, että asiat pysähtyvät ennemmin tai myöhemmin.

Vastaus tähän näennäiseen ristiriitaan on kitkaa. Itse asiassa, jos esine siirtyi täysin sileälle pinnalle, se voisi tehdä sen toistaiseksi, jos mikään muu voima ei vaihda liikettä.

Koska kitkaa on mahdotonta poistaa kokonaan, tilanne, jossa vartalo liikkuu määräämättömäksi ajaksi, on idealisointi.

Lopuksi on tärkeää huomata, että vaikka nettovoima on tyhjä, tämä ei välttämättä edusta voimien kokonaista puuttumista esineeseen.

Maapallon pinnan esineet kokevat aina gravitaatiota vetovoiman. Pöydällä tuettu lepokirja pysyy näin, koska taulukon pinta käyttää voimaa, joka estää painoa.

Newtonin toinen laki

Selitys Newtonin toisesta laista. Lähde: Itse tehty.

Newtonin ensimmäisessä laissa on todettu, mitä tapahtuu kohteelle, jolla verkko tai tuloksena oleva voima on mitätön. Nyt Newtonin dynamiikan tai toisen lain peruslaki osoittaa, mitä tapahtuu, kun nettovoimaa ei kumota:

Jos ulkoinen verkkovoima F Se vaikuttaa massa m: n kohteeseen, se kokee kiihtyvyyden, joka on verrannollinen voimaan ja samaan suuntaan. Matemaattisesti:

F_Netto = m-lla.

Itse asiassa mitä suurempi sovellettu voima, sitä suurempi objektin nopeuden muutos. Ja jos sama voima koskee eri massojen esineitä, kevyempi ja helpompi liikuttaa suuria muutoksia. Päivittäinen kokemus on näiden väitteiden kanssa.

Newtonin kolmas laki

Avaruusraketti saa tarvittavan työntövoiman karkotettujen kaasujen ansiosta. Lähde: Pixabay.

Newtonin kaksi ensimmäistä laki viittaavat yhteen objektiin. Mutta kolmas laki viittaa kaksi esineet. Nimetämme ne esineeksi 1 ja esine 2:

Vuorovaikutuksessa kaksi esinettä, toisiaan käyttävät voimat, ovat aina yhtä suuret ja suuntaan, mutta päinvastainen, mikä matemaattisella tavalla ilmaistaan ​​seuraavasti:

F₁₂ = -F_{kaksikymmentäyksi}

Itse asiassa aina kun voima vaikuttaa ruumiin, se johtuu siitä, että se on vastuussa sen aiheuttamisesta. Siten maan päällä olevilla esineillä on paino, koska se houkuttelee heitä kohti keskustaan. Sähkövaraus hylätään toisen saman merkin kuormituksella, koska se kohdistaa harrastamisvoiman ensimmäiseen, ja siten siten.

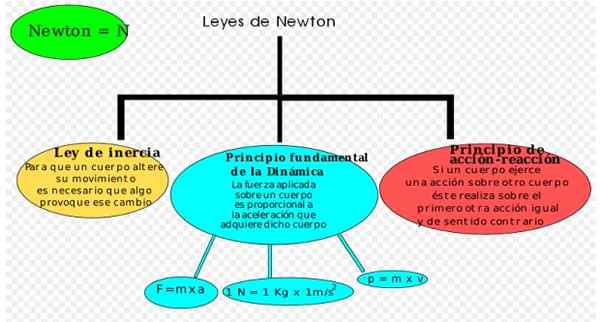Kuva 3. Newtonin lakiyhteenveto. Lähde: Wikimedia Commons. Hugo4914 [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)].

Säilyttämisperiaatteet

Dynamiikassa on useita määriä, jotka säilyvät liikkeen aikana ja joiden tutkimus on perustavanlaatuinen. Ne ovat kuin vankka sarake, johon on mahdollista ratkaista ongelmat, joissa voimat vaihtelevat hyvin monimutkaisista tavoista.

Esimerkki: Juuri kun kaksi ajoneuvoa törmää, niiden välinen vuorovaikutus on erittäin voimakas, mutta lyhyt. Niin voimakas, että muut voimat on otettava huomioon, siksi ajoneuvoja voidaan pitää erillisenä järjestelmänä.

Mutta tämän intensiivisen vuorovaikutuksen kuvaaminen ei ole helppo tehtävä, koska kyse on voimista, jotka vaihtelevat ajan myötä ja myös avaruudessa. Olettaen kuitenkin, että ajoneuvot muodostavat eristetyn järjestelmän, kahden väliset voimat ovat sisäisiä ja liikkumisen määrä säilytetään.

Se voi palvella sinua: Ortonormal Base: Ominaisuudet, esimerkit ja harjoitukset

Liikkeen määrän pitäminen on mahdollista ennustaa, kuinka ajoneuvot liikkuvat heti törmäyksen jälkeen.

Alla on kaksi tärkeintä dynamiikan säilyttämisperiaatetta:

Energiansäästö

Luonnossa erotetaan kahta tyyppiä: konservatiiviset ja ei -konservatiiviset. Paino on hyvä esimerkki entisestä, kun taas kitka on jälkimmäinen.

Konservatiiviset voimat on karakterisoitu, koska ne tarjoavat mahdollisuuden tallentaa energiaa järjestelmän kokoonpanossa. Onko niin kutsuttu potentiaalienergia.

Kun keholla on potentiaalista energiaa konservatiivisen voiman, kuten painon, ja liikkeeseen pääsyn vaikutuksen ansiosta, tällaisesta potentiaalisesta energiasta on tulossa kineettinen energia. Molempien energioiden summaa kutsutaan järjestelmän mekaaniseksi energiaksi ja se on säilytetty, ts. Se pysyy vakiona.

Olla TAI Mahdollinen energia, K -k - kineettinen energia ja JA_m Mekaaninen energia. Jos toimit esineen konservatiivisten voimien parissa, se täyttyy:

JA_m = U + k = vakio

Siksi:

JA_{m alkukirjain} = E_{m lopullinen}

Liikkeen määrän säilyttäminen

Tätä periaatetta sovelletaan paitsi, että kaksi ajoneuvoa törmää. Se on fysiikan laki, jolla on laajuus, joka ylittää makroskooppisen maailman.

Liikkeen määrä säilytetään aurinko-, tähti- ja galaksijärjestelmien tasolla. Ja hän tekee sen myös atomilla ja atomi -ytimellä, huolimatta siitä, että Newtonin mekaniikka lakkaa olemasta pätevä.

Olla P Annetun liikkeen vektorimäärän:

P = m.v

Johdettava P Ajan suhteen:

d -dP /dt = d [m.v]/dt

Jos taikina pysyy vakiona:

d -dP /dt = m dv/dt = m.-lla

Siksi voimme kirjoittaa Newtonin toisen lain tällä tavalla:

F_Netto = DP /DT

Jos kaksi ruumista m₁ ja m₂ Ne muodostavat eristetyn järjestelmän, heidän väliset voimat ovat sisäisiä ja Newtonin kolmannen lain mukaan ne ovat samat ja vastakkaiset F₁ = -F₂, täyttyminen:

d -dP₁ /dt = - dP₂/DT → D [P₁ + P₂]/dt = 0 -

Jos johdannainen suhteessa suuruusluokkaan on tyhjä, se tarkoittaa, että tällainen suuruus pysyy vakiona. Siksi eristetyssä järjestelmässä voidaan vahvistaa, että järjestelmän liikkumisen määrä säilyy:

P₁ + P₂ = vakio

Jopa niin, P₁ ja P₂ Ne voivat vaihdella erikseen. Järjestelmän liikkumisen määrä voidaan jakaa uudelleen, mutta tärkeätä on, että sen summa pysyy ennallaan.

Aloitti konseptit dynamiikassa

Dynamiikassa on monia tärkeitä käsitteitä, mutta kaksi niistä erottuvat: massa ja voima. Joukolla se jo mainittiin aiemmin, ja sitten on luettelo näkyvimmistä käsitteistä, jotka ilmestyvät sen kanssa dynamiikan tutkimuksessa:

Inertia

Se on ominaisuus, että esineiden on vastustettava lepo- tai liikkeen tilassa olevia muutoksia. Kaikilla massa -esineillä on hitaus ja heillä on kokenut hyvin usein, esimerkiksi matkustajat, jotka matkustavat autossa, matkustajat pysyvät levossa, jota pidetään tunteena pysyä istuimen varmuuskopiossa.

Ja jos auto pysähtyy voimakkaasti, matkustajilla on taipumus jättää Brucesia seuraavan eteenpäin suuntautuvan liikkeen jälkeen, joten on tärkeää kuljettaa turvavyöjä aina.

Kuva 4. Autolla matkustettaessa hitaus saa meidät menemään Brucesista, kun autojarrut jyrkästi. Lähde: Pixabay.

Massa

Massa on hitausmitta, koska mitä suurempi kehon massa on, sitä vaikeampaa on siirtää sitä tai tehdä sen liikkeenmuutos. Massa on skalaarinen määrä, tämä tarkoittaa, että rungon massan määrittämiseksi on tarpeen antaa numeerinen arvo sekä valittu yksikkö, joka voi olla kiloja, puntia, grammia ja paljon muuta.

Voi palvella sinua: Lenz Law: Formula, yhtälöt, sovellukset, esimerkit

Paino

Paino on voima, jolla maa houkuttelee keskustaan, esineet, jotka ovat lähellä pintaa.

Koska se on voima, paino on vektor.

Siten, vaikka siihen liittyvä paino ja massa eivät ole samoja, edes vastaavia, koska ensimmäinen on vektori ja toinen skalaari.

Viitejärjestelmät

Liikkeen kuvaus voi vaihdella valitun viitteen mukaan. Ne, jotka nousevat hissiin.

Jos ruumis kokee liikkeen viitekehystä, mutta toisessa on levossa, Newtonin lakia ei voida soveltaa molemmille. Itse asiassa Newtonin lakeja sovelletaan tiettyihin viitejärjestelmiin: ne, jotka ovat inertialaisia.

Siinä inertiaaliset vertailujärjestelmät, Kehot eivät kiihdytä, elleivät niitä häiritä jollain tavalla -joustavat voiman-.

Kuvitteelliset voimat

Kuvitteelliset tai pseudovoimat ilmestyvät, kun ruumiin liike analysoidaan kiihdytetyssä viitekehyksessä. Kuvitteellinen voima erotetaan, koska hänen ulkonäkönsä vastuussa olevaa edustajaa ei ole mahdollista tunnistaa.

Keskipakovoima on hyvä esimerkki kuvitteellisesta voimasta. Se, että se on, ei tee siitä vähemmän todellista niille, jotka kokevat sen kääntyessään autoihinsa, ja tuntevat, että näkymätön käsi työntää heidät pois käyrästä.

Kiihtyvyys

Tämä tärkeä vektori mainittiin jo aiemmin. Kohde kokee kiihtyvyyttä niin kauan kuin on voimaa, joka muuttaa sen nopeutta.

Työ- ja energia

Kun voima toimii esineeseen ja se muuttaa asemaansa, voima on tehnyt työn. Ja tämä työ voidaan varastoida energiamuodossa. Siksi esineelle tehdään työtä, jonka ansiosta se hankkii energiaa.

Seuraava esimerkki selventää pistettä: Oletetaan, että henkilö nostaa potin tietyn korkeuden lattiatason yläpuolelle.

Tätä varten sinun on sovellettava voima ja voitettava painovoima, siksi tehdään työtä potissa ja tämä työ on varastoitu potissa olevaan painovoimapotentiaalienergiaan, verrannollinen sen massaan ja korkeuteen, jonka se saavutti Lattia:

U = m.g.h

Missä m Se on taikina, g Se on painovoima ja h On korkeus. Mitä potti voi tehdä, kun se on valmis h? No, se voi pudota ja kun se putoaa, sen painovoimapotentiaalienergia on vähentynyt, kun taas kineettinen tai liikkeen energia kasvaa.

Jotta voima tekee työtä, on välttämätöntä tuottaa siirtymä, jonka on oltava yhdensuuntainen voiman kanssa. Jos näin ei tapahdu, voima toimii edelleen esineeseen, mutta ei toimi sen kanssa.

liittyvät aiheet

Newtonin ensimmäinen laki.

Newtonin toinen laki.

Newtonin kolmas laki.

Aineensuojelulaki.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6. ... Ed Prentice Hall.
4. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.
5. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. Kuudes lyhennetty painos. Cengage -oppiminen.
6. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa.  Pearson.
7. Wikipedia. Dynaaminen. Palautettu: on.Wikipedia.org.