Taajuusjakauma Kuinka tehdä taulukko, esimerkki, harjoitus

Eräs Taajuusjakauma Tilastoissa se viittaa ryhmissä, luokissa tai luokissa järjestetyn tiedon seuraavaan suuntaukseen, kun jokaiselle on määritetty numero, jota kutsutaan taajuuksille, mikä osoittaa, kuinka monta tietoa jokaisessa ryhmässä on. 

Pääsääntöisesti havaitaan, että nämä taajuudet jakautuvat keskusryhmän ympärille: se, jolla on eniten tietoja.

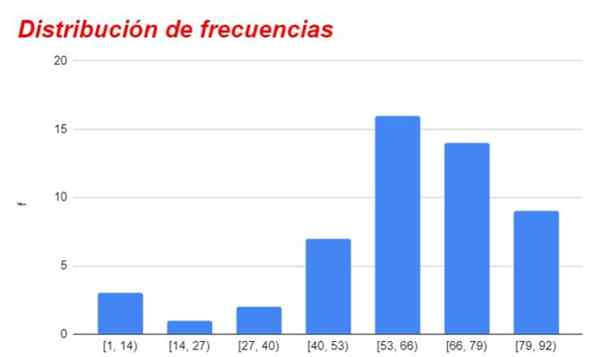
Kuvio 1. Taajuusjakaumakaavio, joka on saatu vastaavasta taulukosta. Lähde: f. Zapata.

Ryhmät, jotka ovat mainitun keskusluokan ylä- tai alapuolella.

Tietojoukon taajuusjakauma tapa koostuu ensin luokkien luomisesta ja sitten taajuustaulukon tekemisestä. Taajuustaulukon visuaalista esitystä kutsutaan histogrammiksi.

[TOC]

Taajuustyypit

Taajuuksia on useita tyyppejä:

1.- Absoluuttinen freekuusia: Se on perusteellisin, ja siitä muut ovat rakennettuja. Se koostuu yksinkertaisesti luokkaa vastaavien tietojen kokonaismäärästä.

2.- Suhteellinen taajuus: Se on kunkin luokan absoluuttinen taajuus jaettuna tietojen kokonaismäärällä.

3.- Prosenttitaajuus: Se on sama suhteellinen taajuus, mutta kerrottuna sata, mikä osoittaa arvojen ulkoasun prosentuaalista ulkonäköä jokaisessa luokassa.

4.- Kertynyt taajuus: Se on luokkien absoluuttisten taajuuksien summa tai yhtä suuri kuin luokka, jota harkitaan. 

5.- Prosenttiosuus kertynyt taajuus: Se on luokkien prosentuaalisten taajuuksien summa alhaisempi tai yhtä suuri kuin luokka, jota havaitaan.

Vaiheet taajuuden jakelupöydän tekemiseen

Taajuusjakelupöydän rakentamiseksi on noudatettava useita vaiheita.

Ensinnäkin puun tietojen, jne.

Voi palvella sinua: mitkä ovat 30? (Selitys)

Vaihe 1

Tunnista vähimmäisarvo Xmin ja enimmäisarvo Xmax Tietojoukossa x.

Vaihe 2

Laske R -alue, joka on määritelty erona maksimiarvon välillä vähemmän minimiarvo: r = xmax - xmin.

Vaihe 3

Määritä numero k -k - väliajoja tai luokkia, jotka voivat olla ennalta sijoitettuja. Numero k -k - määrittää rivien lukumäärän, jotka taajuustaulukossa on.

Vaihe 4

Jos aikavälejä k -k - Sitä ei ole aikaisemmin annettu, niin se on määritettävä seuraavien ohjeiden mukaisesti: suositeltujen luokkien vähiten määrä on 5, mutta se voi olla suurempi, jolloin on parempi valita pariton luku.

Vaihe 5

On kaava nimeltään Sturges -hallinto Se antaa meille väliajojen lukumäärän k -k - suositellaan sarjaan, joka koostuu N Tiedot:

K = [1 + 3,322⋅log n]

Koska kannattimessa on varmasti todellinen luku, kiinnike osoittaa, että se on pyöristettävä lähimpään parittomaan kokonaislukuun kokonaisluvun arvon saamiseksi k -k -.

Vaihe 6

Amplitudi lasketaan -Lla kunkin aikavälin (luokat tai luokat), jotka ottavat osamäärän alueen välillä R - ja väliajojen lukumäärä k -k -- A = r/k. Jos alkuperäiset tiedot ovat kokonaisia ​​numeroita, lähin kokonaisluku on pyöristetty, muuten sen todellinen arvo on jäljellä.

Vaihe 7

Määritä kunkin aikavälin tai luokan ala- ja ylärajat. Ensimmäisellä aikavälillä tai alhaisimmalla luokalla on alaraja pienin alkuperäisistä tiedoista, ts. Li = Xmin ja ylärajaksi vähimmäisarvo plus väliajan amplitudi, tämä on LS = Xmin + A. 

Vaihe 8

Peräkkäiset välit ovat: 

[[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅a), ... [ Xmin + (k-1) a, xmin + k⋅a-A.

Voi palvella sinua: yhdistetyt toiminnot

Vaihe 9

XC -luokan tuotemerkki määritetään jokaiselle aikavälille käyttämällä seuraavaa kaavaa: Xc = (ls - li) / 2 + li.

Vaihe 10

Taajuuspöydän otsikko on sijoitettu, joka koostuu seuraavista tarroista: luokat, XC -luokan tuotemerkki, taajuus F, suhteellinen taajuus F (tai prosentuaalinen taajuus F%) ja kertynyt taajuus F (tai kertynyt prosenttiosuus F%).

Seuraavaksi on seuraava:

Taajuustaulukon ensimmäinen sarake: Sisältää välit tai luokat, joihin tiedot on jaettu.

Toinen sarake: Sisältää kunkin alaryhmän luokan tuotemerkin (tai keskipisteen).

Kolmas sarake: Sisältää kunkin luokan tai luokan absoluuttisen taajuuden F.

Neljäs ja viides sarake: Arvot, jotka vastaavat suhteellista (tai prosentuaalista) taajuutta ja kertynyttä taajuutta F (tai kertynyt prosenttiosuus).

Taulukon rakennusesimerkki

Seuraavat tiedot vastaavat 52 opiskelijan ryhmään sovelletun 100 kysymyksen tarkkoja vastauksia:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

Seuraamme taajuustaulukon rakentaaksesi vaiheita:

1.- Minimi- ja maksimiarvot xmin = 1, xmax = 89.

2.- Alue on: r = 89 - 1 = 88

3.- Väliajojen lukumäärän määrittäminen Sturges -hallinto- K = [1 + 3,322⋅log 52] = [6,70] = 7.

4.- Väliajojen leveyden laskeminen: A = r / k = 88/7 = 12,57 ≈ 13.

5.- Väliajat ovat: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- Kunkin aikavälin luokkamerkit määritetään: 8, 21, 34, 47, 60, 73 ja 86.

7.- Taulukko on tehty:

Voi palvella sinua: sisäiset ja ulkoiset konjugaattikulmat: esimerkkejä, harjoituksia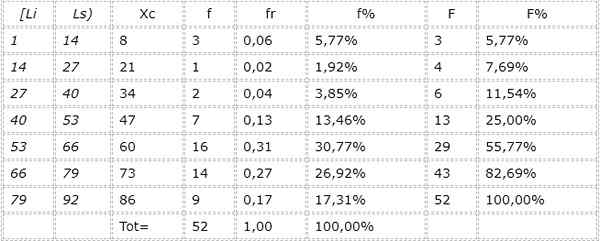

Eri väliajojen tai luokkien taajuuksien kaavio on esitetty kuvassa 1.

Liikuntaa

Opettaja tallentaa fysiikan aiheessa saavutettujen tavoitteiden prosenttiosuuden jokaiselle opiskelijalle. Kunkin opiskelijan pätevyys, vaikka se riippuu saavutettujen tavoitteiden prosenttiosuudesta, on kuitenkin tiukka tietyille luokille, jotka ovat aiemmin vahvistettuja yliopistotutkimuksissa.

Tarkastellaan tiettyä tapausta: fysiikkaosiossa sinulla on prosentuaalinen tavoitteet jokaiselle 52 opiskelijalle: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

Tässä esimerkissä luokat tai luokat vastaavat lopullista pätevyyttä, joka on määritetty saavutettujen tavoitteiden prosenttiosuuden x mukaisesti:

1.- Erittäin huono: 1 ≤ x < 30

2.- Huono: 30 ≤ x < 50

3.- Tarpeeksi: 50 ≤ x < 70

4.- No: 70 ≤ x < 85

5.- Erinomainen: 85 ≤ x ≤ 100

Taajuustaulukon tekemiseksi tiedot tilataan vähiten suurimmaksi ja kertoo kuinka monta tietoa vastaa kutakin luokkaa, joka on pätevyys, jonka opiskelija saa fysiikassa:

1.- Erittäin köyhä: 4 opiskelijaa.

2.- Huono: 6 opiskelijaa.

3.- Tarpeeksi: 20 opiskelijaa.

4.- No: 17 opiskelijaa.

5.- Erinomainen: 5 opiskelijaa.

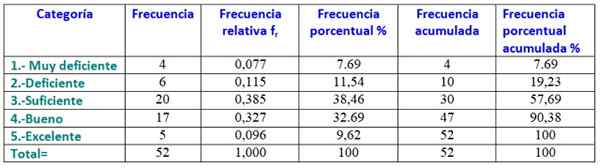
Alla on luokkien histogrammi, rakennettu edellisestä taulukosta:

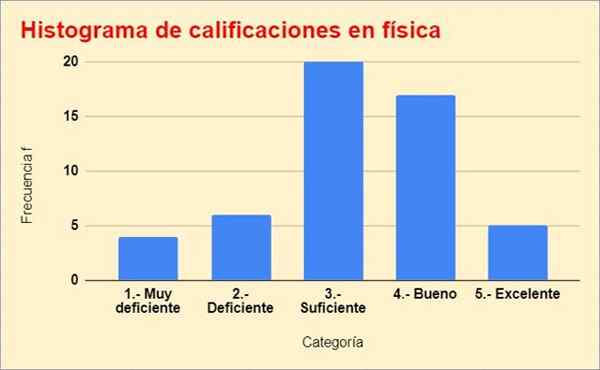Kuva 2. Harjoituksen taajuuden jakautumiskaavio ratkaistu. Lähde: f. Zapata.

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
4. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
5. Spiegel, M. 2009. Tilastot. Schaum -sarja. 4 ta. Painos. McGraw Hill.
6. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.