Fourier -sarjan sovellukset, esimerkit ja harjoitukset ratkaistu

Se Fourier -sarja Ne koostuvat äärettömien termejen summasta, jotka koostuvat harmonisista toiminnoista, sinus ja kosini, joiden argumentti on kokonaisvaltainen perustaajuuden perusta.

Sine- ja kosinifunktiot kerrotaan arvokertoimilla siten, että summa on identtinen funktion kanssa, jonka ajan T on yhtä suuri kuin kahdesti pi (2π) jaettuna kulmataajuudella ω ω ω ω.

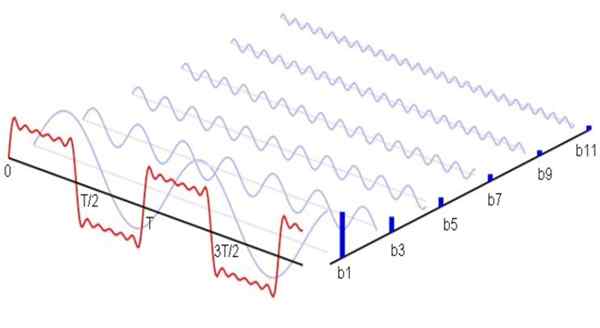
Kuvio 1. Tässä ovat (sinisellä) Fourier -sarjan ensimmäiset nolla -harmonikat, jotka vastaavat neliömäistä aaltomuodoista signaalia. Nämä harmoniset summat aiheuttavat punaisen signaalin. Lähde: Wikimedia Commons.

Matemaattisesti se ilmaistaan ​​seuraavasti: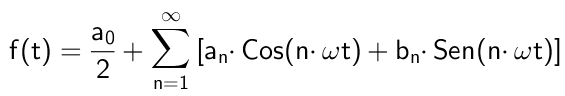

Missä Ω Se on perustaajuus, joka liittyy ajanjaksoon T toiminnasta f (t) Suhteen kautta: 

Ω = 2π / t

Määräaikaiseksi ajanjaksolle T, toiminto f (t) täyttää tämän ehdon:

f (t) = f (t + k t)

Missä k -k - Se on kokonaisluku ja kertoimet_{0 -} , -lla_n ja b_n Niitä kutsutaan Fourier -kertoimet.

[TOC]

Fourier -sarjan merkitys ja käyttö

Fourier -sarjan nimi johtuu siitä, että hänen löytäjänsä oli ranskalainen matemaattinen.

Tämä löytö oli olennaista matematiikasta, koska jos differentiaaliyhtälöllä on tietty harmoninen ratkaisu, niin on mahdollista saavuttaa yleinen ratkaisu päällekkäisyyden tai saman summan avulla.

Fourierin kertoimet jaksollisesta toiminnasta, jota kutsutaan myös merkki, Ne ovat saman spektri.

Siksi spektri on taajuuksien joukko, jotka muodostavat signaalin, jolle on ominaista kunkin taajuuden amplitudi, joka vastaa Fourierin kertoimien arvoja.

Signaalin pakkausjärjestelmät tai ääni- ja video -aaltomuodot, takana huomattavasti pienempi bittien lukumäärä kuin alkuperäinen digitoitu signaali.

Signaalin Fourier -sarja on kuin sormenjälki siinä mielessä.

Vaikka Fourier -sarjan tai sen yleisimmän muodon käyttö Fourier Transform, Signaalin pakkausmenetelmänä se on ollut tiedossa jo jonkin aikaa, sen käytön piti odottaa numeerisia prosessoreita riittävän nopeasti, mikä mahdollisti signaalien puristamisen ja purkamisen "reaaliajassa".

Voi palvella sinua: Tilastolliset muuttujat

Fourier -sarjan esimerkki 

Seuraavaksi esimerkki f (t) -toiminnosta ja sen Fourier -sarjasta.

Toiminto on:

 f (t) = 0 kyllä ​​0 ≤ t  < π y 1 si π ≤  t   < 2π

Ja sen vastaava Fourier -sarja on antanut:

f (t) = ½ - 2/π⋅Se (t) - 2/(3π) ⋅se (3T) - 2/(5π) ⋅sen (5T) - 2/(7π) ⋅sen (7T) -……

Seuraava kuva näyttää Fourier -sarjan funktion ja osittaisen summan:

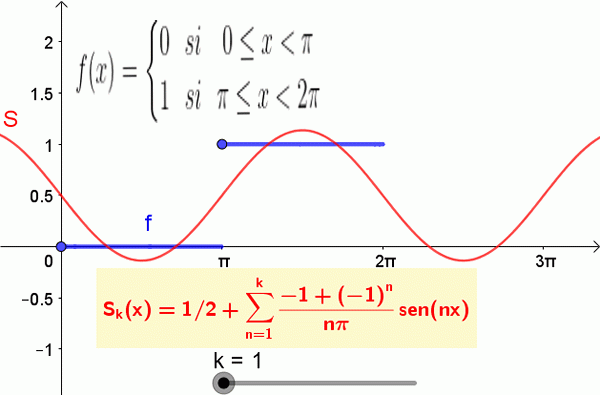Kuva 2. Vaihefunktiota vastaavan Fourierin ensimmäiset 19 termit on esitetty. Lähde: f. Zapata.

Kertoimien määrittäminen

Alla on kuinka määrittää Fourierin kertoimet:

Oletetaan, että funktio on f (x) määritelty välittömästi_Yllyttää t_Yllyttää + T, missä pääoma on toiminnon ajanjakso. Sitten hänen Fourier -sarja on:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 ω t) +… + a_n Cos (n ω t) +…

.. .+ B₁ sin (ω t) +b₂ sin (2 ω t) +… +b_n Synti (n ω t) +..

Riippumattoman termin laskeminen

Riippumattoman termin löytämiseksi integroimme molemmat tasa -arvon jäsenet funktion määritelmän aikavälillä:

[t_Yllyttää , t_Yllyttää+ T]

Siksi:

Sama_n ∫cos (n ω t) dt +…

.. .+ B₁ ∫sen (ω t) dt +b₂ ∫sen (2 ω t) dt +… +b_n ∫sen (n ω t) dt +…

Tässä symboli ∫ tarkoittaa integraalia määriteltyä T: stä_Yllyttää t_Yllyttää + T.

Ensimmäisen termin integraali on t, joka arvioidaan sen ylärajatuloksissa:

t_Yllyttää + T

Alarajan t vähennämällä t_Yllyttää, lopullisesti t.

Kaikki muut termit ovat 0, koska nämä ovat kosini- tai sinusfunktioita, jotka on arvioitu koko ajanjaksolla, kuten alla esitetään:

∫cos (nω t) dt = (1/ nω) ∫cos (nω t) d (nω t)

Muista, että symboli ∫ tarkoittaa integraatiota t: n välillä_Yllyttää t_Yllyttää + T. 

Jotta kosinini tai rinnot ovat integroineet, teemme seuraavan muuttujan muutoksen:

x = ω (t - t_Yllyttää-A

Joten x, dx -ero on yhtä suuri kuin d (ωt) -erot.

Joten suoritettava olennainen on:

Koska N on kokonaisluku, niin määritelty integraali antaa aina nollan. Sama pätee sinifunktioon.

Siksi kaikkien termien täydellisen ajanjakson määritelty integraali. 

Voi palvella sinua: Divisions, jossa jäännös on 300

Siksi päätellään, että termi A₀ lasketaan seuraavasti:

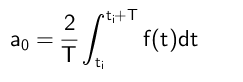
Kertoimien laskenta

Kosinifunktioiden kertoimien kertoimien laskemiseksi molemmat tasa -arvon jäsenet on kerrottava:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 ω t) +… + a_n Cos (n ω t) +…

.. .+ B₁ sin (ω t) +b₂ sin (2 ω t) +… +b_n Synti (n ω t) +..

Sovelletaan kosininfunktiota, joka arvioidaan vastaavassa harmonisessa harmonisessa harmonisessa, ja sitten sovelletaan koko ajanjaksona. 

Esimerkiksi laskea_m Molemmat jäsenet kerrotaan cos (mωt):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) +… + -lla_n Cos (n ω t) cos (m ω t) +…

.. .+ B₁ sin (ω t) cos (m ω t) +b₂ sin (2 ω t) cos (m ω t) +… +b_n Sin (n ω t) cos (m ω t) +..

Integroitu sitten täydelliseen ajanjaksoon, ts_Yllyttää t_Yllyttää + T.

A₀ sisältävän termin integraali peruutetaan, koska M on kokonaisluku ja kosini -toiminto on integroitu koko ajanjaksoon. 

Integraalit, jotka sisältävät tuotteen cos (n ω t) cos (m ω t), on myös mitätöidaan aina kun n ≠ m. Vain siinä tapauksessa, että n = m on olennainen:

Kaikki termit, joilla on kosinus kerrottuna sinus, toisin sanoen B: n kertoimilla kerrottuna, koska SEN -tyypin (n ω t) cos (m ω t) sisältävät integraalit peruutetaan, kun määritelty integraali tehdään täydellisellä ajanjakso. 

Tästä eteenpäin on päätelty, että:

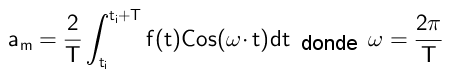
Kertoimien B laskeminen

B: n kertoimien löytämiseksi sovelletaan samanlaista menettelyä, mutta tällä kertaa Fourier -sarjaan sovitetut funktion jäsenet kerrotaan sen funktiolla (M ω T).

Samoista syistä, jotka on jo selitetty tapaukseen, jossa ainoa termi, jota ei kumota integroitumisen jälkeen täydelliseen ajanjaksoon, on sellainen, jossa:

n = m

Ja missä [SEN (M ω T)] on integraali², joka integroitu koko ajanjaksona johtaa π.

Voi palvella sinua: Homografinen toiminto: Kuinka kuvaaja, ratkaistut harjoitukset

Tällä tavalla B: n kertoimet lasketaan seuraavan kaavan mukaan:

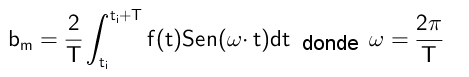
Harjoitukset

- Harjoitus 1

Tee funktion kertoimien nimenomainen laskelma

 f (t) = 0 kyllä ​​0 ≤ t  < π y 1 si π ≤  t   < 2π

Ratkaisu

Ensin tunnistamme tämän toiminnon ajan t: n 2π: ksi, joten tässä esimerkissä perustaajuus ω = 2π/ t on yhtä suuri kuin yksikkö, ts

Ω = 1

Funktio määritetään aikavälillä [0, 2π], joten kaikki integraatiot suoritetaan mainitulla aikavälillä. 

Sitten riippumaton termi lasketaan seuraavasti:

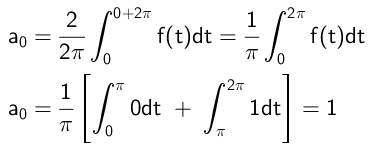
Kosinifunktioihin moninkertaistuvat kertoimet lasketaan tällä tavalla:

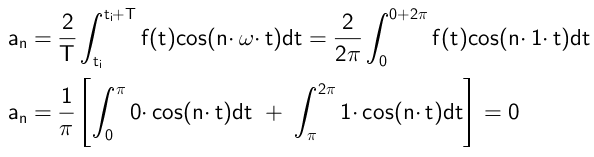
Kuten voidaan nähdä, kaikki kertoimet ovat nollaa, mikä tapahtuu, mikäli funktio f (t) on pariton.

Samoin B: n kertoimet lasketaan seuraavasti:

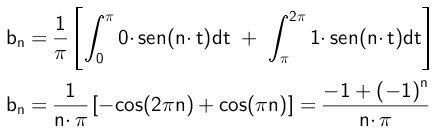
- Harjoitus 2

Etsi funktion kertoimet, jotka vastaavat kuvaa 1, joka on:

f (t) = -1 kyllä ​​0≤ t

Ratkaisu 

Kun funktio ottaa arvot välillä -1 ja +1, voimme intuitiota, että riippumaton termi on tyhjä, mutta laskemme sen nimenomaisesti:

Koska funktiolla on pariton symmetria, kaikki kertoimet, jotka kertovat harmoniset termit kosinifunktion kanssa. Varmistamme sen alla:

Lopuksi löydämme B: n kertoimet, jotka kertovat sinusfunktion sisältävät harmoniset termit:

Missä kaikki B: n ehdot, joiden alaindeksi voidaan huomata, ovat 0. Ensimmäiset parittomat termit ovat:

b -₁= -4/(π); b -₃= -4/(3π); b -₅= -4/(5π); b -₇= -4/(7π) ja B₉= -4/(9π)

https: // youtu.Be/737yagwszya

Viitteet

1. Imerror, i. 2013. Diskreetin Fourier -muunnoksen hallitseminen yhdessä, kahdessa tai useammassa ulottuvuudessa: sudenkuopat ja esineet. Springer Science & Business Media.
2. Briggs, W. tuhatyhdeksänsataayhdeksänkymmentäviisi. DFT: Omistajien käsikirja erilliselle Fourier -muunnolle. Siam.
3. Chu, e. 2008. Diskreetti ja jatkuvat Fourier -muunnokset: analyysi, sovellukset ja nopeat algoritmit. CRC -lehdistö.
4. Guoan Bi, Yonghong Zeng. 2012. Muunnokset ja nopeat algoritmit signaalianalyysiä ja esityksiä varten. Springer Science & Business Media.
5. Sundararajan, D. 2003. Digitaalinen signaalinkäsittely: teoria ja käytäntö.Maailman tieteellinen. 
6. Wikipedia. Fourier -sarja. Palautettu: on.Wikipedia.com