Mikä on deterministinen kokeilu?

Hän deterministinen koe, Tilastoissa se on ennustettavissa oleva ja toistettava tulos, kunhan samat alkuolosuhteet ja parametrit ylläpidetään. Eli syy-seuraussuhde tunnetaan kokonaisuudessaan.

Esimerkiksi aika, joka vie hiekan yhdestä kellosta siirtyäkseen osastosta toiseen, on deterministinen koe, koska tulos on ennustettavissa ja toistettavissa. Niin kauan kuin olosuhteet ovat samat, kapselista kapseliin siirtyminen vie samaan aikaan.

Kuvio 1. Aika, joka vie hiekan yhdestä osastosta toiseen, on deterministinen kokeilu. Lähde: Pixabay

Monet fyysiset ilmiöt ovat deterministisiä, jotkut esimerkit ovat seuraavat:

- Tihein esine kuin vesi, kuten kivi, uppoaa aina.

- Kellu, joka on vähemmän tiheä kuin vesi, on aina pinnalla (ellei sitä pitävää voimaa) käytetään) käytetään).

- Veden kiehumislämpötila merenpinnan tasolla on aina 100 ºC.

- Aika, joka kuluu tietylle, joka putoaa leposta, koska se määritetään sen korkeuden perusteella, josta se pudotettiin, ja tämä aika on aina sama (kun se vapautuu samasta korkeudesta).

Hyödyntämällä noppaa. Jos tämä pudotetaan, vaikka olet varovainen antamaan saman suunnan ja aina samalla korkeudella, on vaikea ennustaa, mitkä kasvot se ilmestyy, kun se on pysähtynyt maahan. Tämä olisi satunnainen koe.

Teoreettisesti, jos ne tunnetaan äärettömällä tarkkuustiedolla, kuten: sijainti; Alkuperäinen nopeus ja noppa -suunta; Muoto (pyöristetyt tai kulmäreunat); ja sen pinnan palauttamiskerroin, jolla se putoaa. Mutta kaikki pienet variaatiot lähtöolosuhteissa antaisi erilaisen tuloksen. 

Tällaiset järjestelmät ovat deterministisiä ja samanaikaisesti kaoottisia, koska alkuolosuhteiden pieni muutos muuttaa lopputulosta satunnaisella tavalla.

Voi palvella sinua: Yhtälöjärjestelmä: ratkaisumenetelmät, esimerkit, harjoitukset

[TOC]

Mittaus

Deterministiset kokeet ovat täysin mitattavissa, mutta sen tuloksen mittaus ei silti ole äärettömän tarkka ja sillä on tietty epävarmuusmarginaali.

Annetaan esimerkiksi seuraava koe, täysin deterministinen: vapauta leluauto suorassa rinteessä.

Kuva 2. Auto laskeutuu suoraviivaisen kaltevuuden läpi deterministisessä kokeessa. Lähde: Pixabay.

Se vapautetaan aina samasta lähtökohdasta, huolehtimaan siitä, ettei se anna mitään impulssia. Tässä tapauksessa radan matkustamiseen kuluva aika, joka vie autolle, on aina oltava sama.

Nyt lapsi aikoo mitata aikaa, jonka hän vie kärräretkelle radalla. Tätä varten käytät sekuntikelloa, joka on sisällytetty matkapuhelimeesi.

Tarkkailijapoika on ensimmäinen asia, jonka huomaat, että mittauslaitteessasi on rajallinen tarkkuus, koska pienin aikaero, joka voi mitata sekuntikelloa, on yksi sata sekuntia.

Sitten lapsi jatkaa kokeilun suorittamista ja liikkuvien sekuntikellojen kanssa 11 kertaa - sanotaan, että varmasti - aika, jonka hän vei lastenrattaalle kallistettujen lentokoneen matkustamiseen, saaden seuraavat tulokset:

3,12s 3,09s 3,04s 3,04s 3,10s 3,08s 3,05s 3,10s 3,11s 3,06s ja 3,03s.

Lapsi on yllättynyt, koska koulussa he olivat kertoneet hänelle, että tämä on deterministinen kokeilu, mutta jokaisessa määrin hän sai hieman erilaisen tuloksen.

Muunnelmat siinä määrin

Mikä voi olla syyt, että jokaisessa mittauksessa on erilainen tulos? 

Syy voi olla instrumentin tarkkuus, joka, kuten se oli jo sanottu, on 0,01 s. Mutta huomaa, että mittausten erot ovat tämän arvon yläpuolella, joten sitä tulisi ajatella muista syistä, kuten:

- Lähtökohdan pienet variaatiot.

- Erot sekuntikelloa alussa ja pysäyttäessä lapsen reaktioajan vuoksi.

Reaktioajan suhteen viivästyminen tapahtuu varmasti, koska lapsi näkee kärryn alkavan liikkua, kunnes sekuntikellot puristuvat. 

Voi palvella sinua: kuution reunat

Samoin saapuessaan on viive reaktioajasta. Mutta käynnistys- ja saapumisviiveet korvataan, joten saadun ajan on oltava hyvin lähellä todellista. 

Joka tapauksessa kompensointi reaktioviiveelle ei ole tarkka, koska reaktioaikoilla voi olla pieniä variaatioita kussakin kokeessa, mikä selittää tulosten erot.

Mikä on sitten kokeen todellinen tulos?

Mittauksen ja virheen tulokset

Lopullisen tuloksen ilmoittamiseksi meidän on käytettävä tilastoja. Katsotaan ensin, kuinka usein tulokset toistetaan:

- 3,03S (1 kerta)

- 3,04 s (2 kertaa)

- 3,05 s (1 kerta)

- 3,06s (1 kerta)

- 3,08s (1 kerta)

- 3,09 s 1 kerta

- 3,10s (2 kertaa)

- 3.11s (1 kerta)

- 3,12S (1 kerta)

Tietoja tilaamalla ymmärrämme, että a muoti tai toistuva tulos. Sitten raportin tulos on aritmeettinen keskiarvo, joka voidaan laskea seuraavasti:

(1 × 3,03 + 2 × 3,04 + 1 × 3,05 + 1x 3.06 + 1 × 3,08 + 1 × 3,09 + 2 × 3,10 + 1 × 3,11 + 1 × 3,12) / (1 + 2 + 1 + 1 + 1 + 1 + 1 + 2 + 1 + 1).

Edellisen laskelman tulos on 3.074545455. Loogisesti, ei ole mitään järkeä ilmoittaa kaikki nämä desimaalit tuloksessa, koska jokaisella mittauksella ei ole mitään plus 2 tarkkuutta desimaalia. 

Pyöristämissääntöjen soveltamisessa voidaan sanoa, että kulkukierrokseen kuluttava aika on pyöristetty aritmeettinen keskiarvo kahteen desimaaliin.

Tulos, jonka voimme ilmoittaa kokeilumme, on:

3,08 sekuntia on aika, jolloin otat leluautolle kaltevan radan.

- Mittausvirhe

Kuten deterministisen kokeen esimerkistämme nähdään, jokaisella mittauksella on virhe, koska sitä ei voida mitata äärettömällä tarkkuudella.

Joka tapauksessa ainoa asia, joka voidaan tehdä, on instrumenttien ja mittausmenetelmien parantaminen tarkemman tuloksen saamiseksi.

Edellisessä osiossa annoimme tuloksen leluautolle silloin, kun leluautolle kuluu kalteva radan matkustaminen. Mutta tämä tulos merkitsee virhettä. Nyt selitämme, miten tämä virhe lasketaan.

Se voi palvella sinua: Suorakulmaiset koordinaatit: Esimerkkejä ja harjoituksia ratkaistu

- Mittausvirheen laskenta

Ajan mittauksissa tehdyissä toimenpiteissä on dispersio. Se keskihajonta Se on usein käytetty tilastollinen lomake tietojen dispersion ilmoittamiseen. 

Varianssi ja keskihajonta

Tapa laskea keskihajonta on sellainen: Ensimmäinen on tällä tavalla määritelty tietojen varianssi:

Kunkin tuloksen erojen summa aritmeettisen keskiarvon kanssa, neliö ja jaettuna tietojen kokonaismäärällä

Jos neliöjuuri viedään varianssiin, saadaan standardipoikkeama.

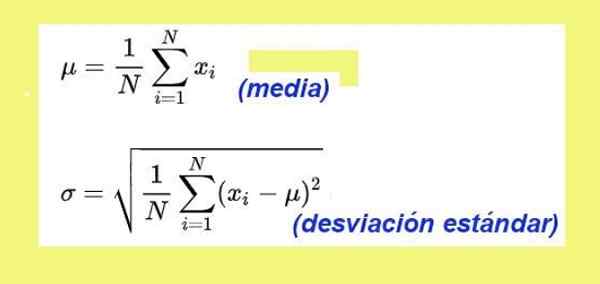Kuva 3. Keskimääräiset kaavat ja keskihajonta. Lähde: Wikimedia Commons.

Lelu -autojen laskeutumisajan datan keskihajonta on:

σ = 0,03

Tulos pyöristettiin 2 desimaaliin, koska kunkin datan tarkkuus on 2 desimaalia. Tässä tapauksessa 0,03s edustaa kunkin datan tilastollista virhettä.

Saatujen aikojen keskimääräinen aritmeettinen keskiarvo on kuitenkin alhaisempi virhe. Keskimääräinen virhe lasketaan jakamalla keskihajonta kokonaistiedon neliöjuuren välillä.

Keskimääräinen virhe = σ / √n = 0,03 / √11 = 0,01

Toisin sanoen keskimääräisen ajan tilastollinen virhe on yksi sadas sekunnista ja tässä esimerkissä se osuu samanaikaisesti sekuntikelloa, mutta se ei aina ole niin.

Mittauksen lopputuloksena siitä ilmoitetaan sitten:

 T = 3,08s ± 0,01 s on aika, joka kuluu leluautoon kaltevan radan matkustamiseen.

Johtopäätöksenä on, että jopa deterministisen kokeen suhteen sen mittauksen tuloksella ei ole ääretöntä tarkkuutta ja sillä on aina virhemarginaali. 

Ja lopputuloksen ilmoittamiseksi se on välttämätöntä, jopa deterministisen kokeen suhteen, käytä tilastollisia menetelmiä.

Viitteet

1. Canalphi. Deterministinen koe. Palautettu: YouTube.com
2. Matematiikka. Deterministinen koe. Palautettu: YouTube.com
3. Pishro Nick H . Johdanto todennäköisyyteen. Haettu: Todennäköisyyskuvaa.com
4. Ross. Insinöörien todennäköisyys ja tilastot. MC-Graw Hill.
5. Tilastot miten. Deterministinen: määritelmä ja kokeet. Palautettu: Statisticshowto.Datascienceceral.com
6. Wikipedia. Tyypillinen poikkeama. Palautettu: on.Wikipedia.com
7. Wikipedia. Koe (todennäköisyysteoria). Haettu: vuonna.Wikipedia.com