Normaali kaavan jakautuminen, ominaisuudet, esimerkki, liikunta

Se normaalijakauma o Gaussin jakauma on todennäköisyysjakauma jatkuvassa muuttujassa, jossa todennäköisyystiheysfunktio kuvataan kvadraattisen ja negatiivisen argumentin eksponentiaalisella funktiolla, mikä johtaa halkeiluun muotoon.

Normaalijakauman nimi tulee siitä tosiasiasta, että tämä jakauma on se, jota sovelletaan eniten tilanteita, joissa jokin jatkuva satunnaismuuttuja on mukana tiettyyn ryhmään tai populaatioon.

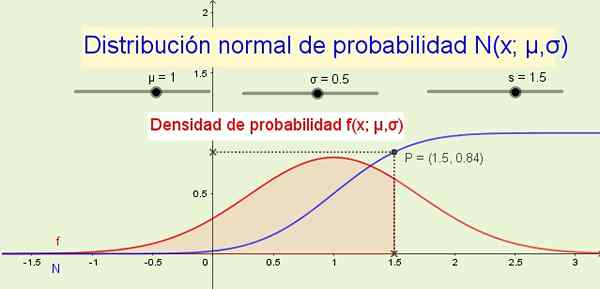
Kuvio 1. Normaalijakauma N (x; μ, σ) ja sen todennäköisyystiheys F (s; μ, σ). (Oma yksityiskohta)

Esimerkkeinä, joissa käytetään normaalia jakautumista: miesten tai naisten korkeus, vaihtelut jonkin fyysisen suuruuden suhteen tai mitattavissa olevissa psykologisissa tai sosiologisissa piirteissä, kuten henkinen osuus tai tietyn tuotteen kulutustottumukset.

Toisaalta sitä kutsutaan Gaussin jakeliksi tai Gauss Belliksi, koska juuri tämä saksalainen matemaattinen nero hyvitetään hänen löytämistään käytöstä, jonka hän antoi tähtitieteellisten mittausten tilastollisen virheen kuvaamiseksi vuonna 1800.

Väitetään kuitenkin, että tämän tilastollisen jakauman julkaisi aikaisemmin toinen ranskalaisen alkuperän matemaatikko, samoin kuin Abraham de Moivre, jo vuonna 1733.

[TOC]

Kaava

Normaaliin jakautumisfunktioon jatkuvassa muuttujassa x, Parametreilla μ ja σ Sitä merkitään:

N (x; μ, σ)

Ja nimenomaisesti se on kirjoitettu näin:

N (x; μ, σ) = ∫_-∞^x f (s; μ, σ) ds

missä f (u; μ, σ) Se on todennäköisyystiheysfunktio:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s²/(2σ²-A

Vakiota, joka kertoo eksponentiaalisen funktion todennäköisyystiheysfunktiossa, kutsutaan normalisointivakioksi, ja se on valittu siten, että:

N (+∞, μ, σ) = 1

Edellinen lauseke varmistaa, että todennäköisyys, että satunnaismuuttuja x olla välillä -∞ ja +∞ joko 1, se on 100% todennäköisyys.

Parametri μ Se on jatkuvan satunnaismuuttujan x aritmeettinen keskiarvo σ Saman muuttujan varianssin keskihajonta tai neliöjuuri. Siinä tapauksessa μ = 0 ja σ = 1 Sinulla on tyypillinen normaali standardi- tai normaalijakaumajakauma: 

N (x; μ = 0, σ = 1-A

Normaalijakaumaominaisuudet

1- Jos satunnainen tilastollinen muuttuja seuraa normaalia todennäköisyystiheyden jakautumista f (s; μ, σ), Suurin osa tiedoista on ryhmitelty keskiarvoon μ Ja ne ovat hajaantuneita heidän ympärillään niin, että vain tiedon yli on välillä μ - σ ja μ + σ. 

Voi palvella sinua: Absoluuttinen taajuus: kaava, laskenta, jakauma, esimerkki

2- Vakiopoikkeama σ Se on aina positiivinen.

3- tiheysfunktion muoto F Se muistuttaa kelloa. 

4- Gaussin jakautumisessa keskimääräinen mediaani ja muoti osuvat.

5- Todennäköisyystiheysfunktion käännepisteet löytyvät tarkasti μ - σ ja μ + σ.

6- F-funktio on symmetrinen suhteessa akseliin, joka kulkee sen keskiarvon mukaan μ Ja sinulla on nolla asymptoottisesti x ⟶ +∞: lle ja x ⟶ -i.

7- korkeampi arvo σ Suurempi leviäminen, melu tai etäisyystiedot keskiarvon ympärillä. Toisin sanoen σ Kellon muoto on avoimempi. Sen sijaan σ Pieni osoittaa, että noppa ui keskiarvoon ja kellon muoto on suljempi tai terävämpi.

8- Jakelufunktio N (x; μ, σ) osoittaa todennäköisyyden, että satunnaismuuttuja on pienempi tai yhtä suuri kuin x. Esimerkiksi kuviossa 1 (yllä) todennäköisyys p, että muuttuja x on vähemmän tai yhtä suuri kuin 1.5 on 84% ja vastaa todennäköisyystiheysfunktion alla olevaa aluetta f (x; μ, σ) - x.

Luottamusvälit

9- Jos tiedot seuraavat normaalia jakaumaa, niin 68,26% näistä on välillä μ - σ ja μ + σ.

10- 95,44% normaalia jakaumaa seuraavista tiedoista on välillä μ - 2σ ja μ + 2σ.

11- 99,74% normaalia jakaumaa seuraavista tiedoista on välillä μ - 3σ ja μ + 3σ.

12- Jos satunnaismuuttuja x Noudattaa jakelua N (x; μ, σ), Sitten muuttuja

Z = (x - μ) / σ  Noudata normaalia normaalia jakaumaa  N (z; 0,1).

Muuttujan muutos x siihen z -z Sitä kutsutaan standardisoinniksi tai tyypilliseksi ja se on erittäin hyödyllinen standardin jakelutaulukoiden soveltamishetkellä tietoihin, jotka seuraavat normaalia epästandardia jakaumaa.

Normaalijakauma -sovellukset

Normaalin jakauman soveltamiseksi on välttämätöntä käydä läpi todennäköisyystiheyden integraali, joka analyyttisestä näkökulmasta ei ole helppoa eikä ole aina käytettävissä tietokoneohjelma, joka mahdollistaa sen numeerisen laskelman. Tätä varten käytetään vakio- tai tyypillistä arvotaulukoita, mikä ei ole muuta kuin normaali jakauma tapauksessa μ = 0 ja σ = 1.

Voi palvella sinua: yhdistetyt toiminnot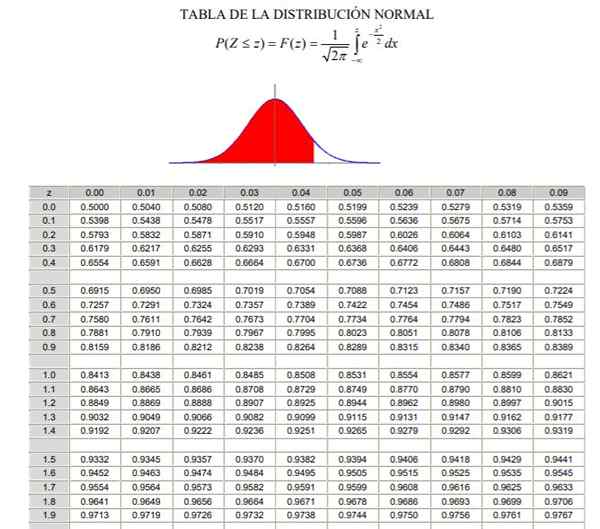Normaalijakaumataulukko tyypillinen (osa 1/2) 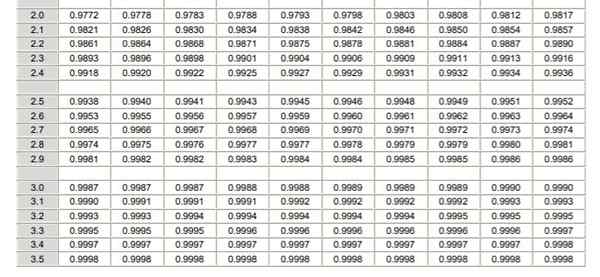Normaalijakaumataulukko tyypillinen (osa 2/2)

On huomattava, että nämä taulukot eivät sisällä negatiivisia arvoja. Kuitenkin käyttämällä Gaussin todennäköisyystiheysfunktion symmetriaominaisuuksia, vastaavat arvot voidaan saada. Taulukon käytön alla olevassa ratkaistussa harjoituksessa on merkitty näissä tapauksissa.

Esimerkki

Oletetaan, että sinulla on satunnainen tietojoukko X, joka seuraa normaalia keskimääräistä jakautumista 10 ja keskihajonta 2. Pyydetään löytämään todennäköisyys, että:

a) satunnaismuuttuja X on pienempi tai yhtä suuri kuin 8.

b) on vähemmän tai yhtä suuri kuin 10.

c) Tämä muuttuja X on alle 12.

d) todennäköisyys, että x -arvo on välillä 8 - 12.

Ratkaisu:

A) Vastaa ensimmäiseen kysymykseen, joka sinun on vain laskettava:

N (x; μ, σ)

Kanssa x = 8, μ = 10 ja σ = 2. Ymmärrämme, että se on olennainen, jolla ei ole analyyttistä ratkaisua alkuainetoiminnoissa, mutta ratkaisu ilmaistaan ​​virhetoiminnon mukaan ERF (x).

Toisaalta on mahdollista ratkaista integraali numeerisella tavalla, mikä on mitä monet laskimet, laskentataulukot ja tietokoneohjelmat, kuten geogebra, tekevät. Seuraava kuva näyttää ensimmäistä tapausta vastaavan numeerisen ratkaisun:

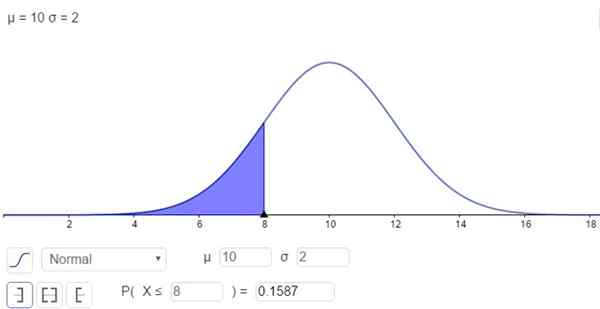Kuva 2. Todennäköisyystiheys F (x; μ, σ). Varjostettu alue edustaa P (x ≤ 8). (Oma yksityiskohta)

Ja vastaus on, että todennäköisyys, että X on alle 8, on:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0,1587

b) Tässä tapauksessa on kyse todennäköisyydestä, että satunnaismuuttuja X on alle keskiarvon, että tässä tapauksessa on 10. Vastaus ei vaadi laskelmaa, koska tiedämme, että puolet tiedoista on alle keskiarvon ja toisen puolen keskiarvon yläpuolella. Siksi vastaus on:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) Vastaa tähän kysymykseen sinun on laskettava N (x = 12; μ = 10, σ = 2), joka voidaan tehdä laskimella, jolla on tilastollisia toimintoja, tai ohjelmistoilla, kuten geogebra:

Voi palvella sinua: 8: 8: Mitkä ovat helppoja selityksiä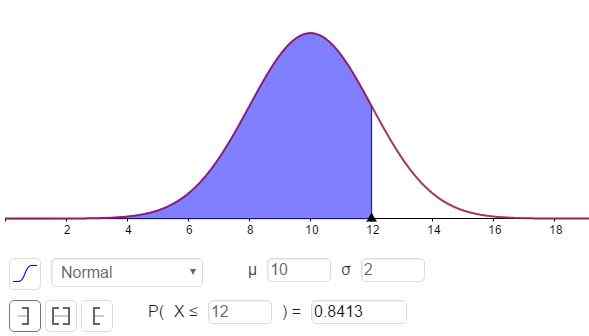Kuva 3. Todennäköisyystiheys F (x; μ, σ). Varjostettu alue edustaa P (x ≤ 12). (Oma yksityiskohta)

Vastaus osaan voidaan nähdä kuvasta 3 ja on:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

d) Löydä todennäköisyys, että satunnaismuuttuja X on välillä 8 - 12, voimme käyttää osien A ja C tuloksia seuraavasti:

P (8 ≤ x ≤ 12) = p (x ≤ 12) - p (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Liikuntaa

Yrityksen osakkeiden keskimääräinen hinta on 25 dollaria, ja keskihajonta on 4 dollaria. Määritä todennäköisyys, että:

a) Toiminta maksaa alle 20 dollaria.

b) sen kustannukset ovat yli 30 dollaria.

c) Hinta on välillä 20–30 dollaria.

Käytä tyypillisiä normaaleja jakelutaulukoita löytääksesi vastaukset.

Ratkaisu:

Taulukoiden hyödyntämiseksi on tarpeen siirtyä normalisoituun tai tyypilliseen muuttujaan:

20 dollaria standardisoidussa muuttujassa on yhtä suuri kuin z = (20 dollaria - 25 dollaria) / 4 dollaria = -5/4 = -1,25 ja 

30 dollaria standardisoidussa muuttujassa on yhtä suuri kuin z = (30 dollaria - 25 dollaria) / 4 dollaria = +5/4 = +1,25.

a) 20 dollaria vastaa -1,25 standardisoidussa muuttujassa, mutta taulukossa ei ole negatiivisia arvoja, joten asetamme +1,25 -arvon, joka näyttää arvon 0,8944.

Jos tämä arvo vähennetään 0,5, tulos on pinta -ala 0 -1,25, joka muuten on identtinen (symmetrialla) alueelle -1 välillä -1.25 ja 0. Vähennystulos on 0,8944 - 0,5 = 0,3944, joka on -1: n välillä -1.25 ja 0.

Mutta pinta -alan kohdasta -∞ --1,25, jotka ovat 0,5 -0,3944 = 0,1056. Siksi päätetään, että todennäköisyys, että toiminta on alle 20 dollaria, on 10,56%.

b) 30 dollaria tyypillisessä muuttujassa Z on 1,25. Tätä taulukon arvoa koskevalle arvolle tulee luku 0.8944, joka vastaa aluetta -∞ -+1.25. +1: n välinen alue.25 y +∞ on (1 - 0,8944) = 0,1056. Toisin sanoen todennäköisyys, että toiminta maksaa yli 30 dollaria, on 10,56%.

c) Todennäköisyys, että toimenpiteellä on kustannukset välillä 20–30 dollaria, lasketaan seuraavasti:

100% -10,56% - 10,56% = 78,88%

Viitteet

1. Tilasto ja todennäköisyys. Normaalijakauma. Haettu osoitteesta: ProjecodesCartes.org
2. Geogebra. Klassinen geogebra, todennäköisyyslaskelma. Toipunut geogebrasta.org
3. Matematiikka. Gauss -jakelu. Palautettu: on.Matematiikka.com
4. Mendenhall, W. 1981. Hallinnon ja taloustieteen tilastot. Kolmas. painos. Iberoamerica -toimitusryhmä.
5. Stat -vaellus. Opeta itsellesi tilastot. Poisson -jakelu. Palautettu: Statstrek.com,
6. Triola, m. 2012. Perustilastot. 11. päivä. Ed. Pearson -koulutus.
7. Vigon yliopisto. Tärkeimmät jatkuvat jakaumat. Toipunut: Anapg.verkkosivustot.Uvigo.On
8. Wikipedia. Normaalijakauma. Palautettu: on.Wikipedia.org